PROBLEM 1 :
What is the value of $(8 \times 4+2)-(8+4 \times 2)$ ?
(A) 0
(B) 6
(C) 10
(D) 18
(E) 24
ANSWER :
(D) 18
PROBLEM 2 :
A square piece of paper is folded twice into four equal quarters, as shown below, then cut along the dashed line. When unfolded, the paper will match which of the following figures?
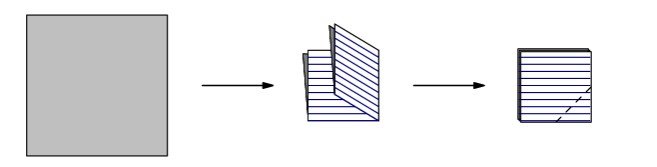
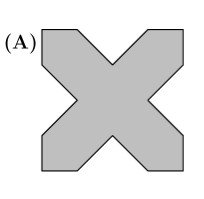

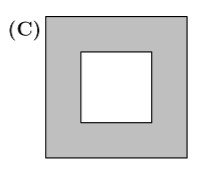
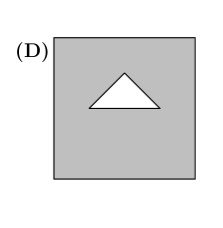

ANSWER :
(E)

PROBLEM 3 :
Wind chill is a measure of how cold people feel when exposed to wind outside. A good estimate for wind chill can be found using this calculation
$$
(\text { wind chill })=(\text { air temperature })-0.7 \times(\text { wind speed }),
$$
where temperature is measured in degrees Fahrenheit ( ${ }^{\circ} \mathrm{F}$ ) and the wind speed is measured in miles per hour (mph). Suppose the air temperature is $36^{\circ} \mathrm{F}$ and the wind speed is 18 mph . Which of the following is closest to the approximate wind chill?
(A) 18
(B) 23
(C) 28
(D) 32
(E) 35
ANSWER :
(B) 23
PROBLEM 4 :
The numbers from 1 to 49 are arranged in a spiral pattern on a square grid, beginning at the center. The first few numbers have been entered into the grid below. Consider the four numbers that will appear in the shaded squares, on the same diagonal as the number 7 . How many of these four numbers are prime?
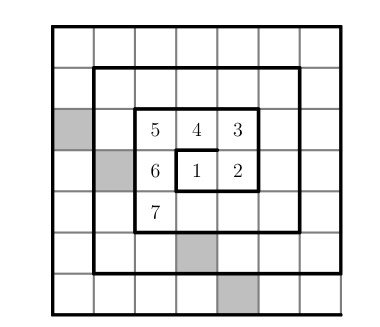
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
ANSWER :
(D) 3
PROBLEM 5 :
A lake contains 250 trout, along with a variety of other fish. When a marine biologist catches and releases a sample of 180 fish from the lake, 30 are identified as trout. Assume that the ratio of trout to the total number of fish is the same in both the sample and the lake. How many fish are there in the lake?
(A) 1250
(B) 1500
(C) 1750
(D) 1800
(E) 2000
ANSWER :
(B) 1500
PROBLEM 6 :
The digits $2,0,2$, and 3 are placed in the expression below, one digit per box. What is the maximum possible value of the expression?

(A) 0
(B) 8
(C) 9
(D) 16
(E) 18
ANSWER :
(C) 9
PROBLEM 7 :
A rectangle, with sides parallel to the $x$-axis and $y$-axis, has opposite vertices located at $(15,3)$ and $(16,5)$. A line is drawn through points $A(0,0)$ and $B(3,1)$. Another line is drawn through points $C(0,10)$ and $D(2,9)$. How many points on the rectangle lie on at least one of the two lines?
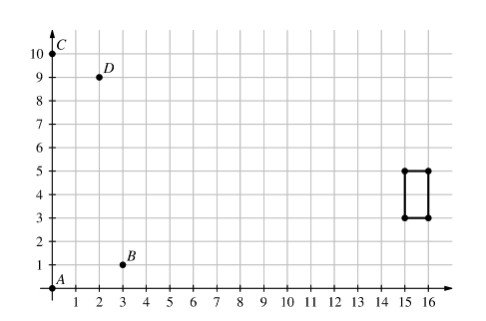
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
ANSWER :
(B) 1
PROBLEM 8 :
Lola, Lolo, Tiya, and Tiyo participated in a ping pong tournament. Each player competed against each of the other three players exactly twice. Shown below are the win-loss records for the players. The numbers 1 and 0 represent a win or loss, respectively. For example, Lola won five matches and lost the fourth match. What was Tiyo's win-loss record?

(A) 000101
(B) 001001
(C) 010000
(D) 010101
(E) 011000
SOLUTION :
(A) 000101
PROBLEM 9 :
Malaika is skiing on a mountain. The graph below shows her elevation, in meters, above the base of the mountain as she skis along a trail. In total, how many seconds does she spend at an elevation between 4 and 7 meters?
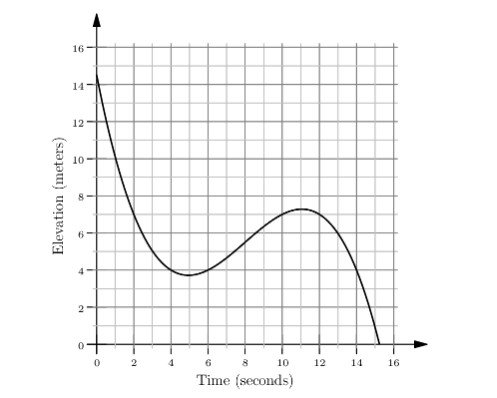
(A) 6
(B) 8
(C) 10
(D) 12
(E) 14
ANSWER :
(B) 8
PROBLEM 10 :
Harold made a plum pie to take on a picnic. He was able to eat only $\frac{1}{4}$ of the pie, and he left the rest for his friends. A moose came by and ate $\frac{1}{3}$ of what Harold left behind. After that, a porcupine ate $\frac{1}{3}$ of what the moose left behind. How much of the original pie still remained after the porcupine left?
(A) $\frac{1}{12}$
(B) $\frac{1}{6}$
(C) $\frac{1}{4}$
(D) $\frac{1}{3}$
(E) $\frac{5}{12}$
ANSWER :
(D) $\frac{1}{3}$
PROBLEM 11 :
NASA's Perseverance Rover was launched on July 30 , 2020. After traveling $292,526,838$ miles, it landed on Mars in Jezero Crater about 6.5 months later. Which of the following is closest to the Rover's average interplanetary speed in miles per hour?
(A) 6,000
(B) 12,000
(C) 60,000
(D) 120,000
(E) 600,000
ANSWER :
(C) 60,000
PROBLEM 12 :
The figure below shows a large white circle with a number of smaller white and shaded circles in its interior. What fraction of the interior of the large white circle is shaded?
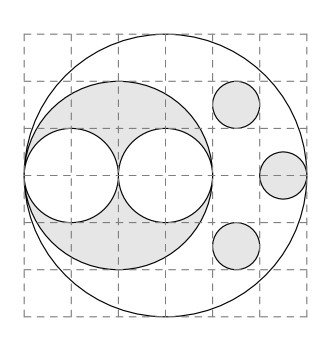
(A) $\frac{1}{4}$
(B) $\frac{11}{36}$
(C) $\frac{1}{3}$
(D) $\frac{19}{36}$
(E) $\frac{5}{9}$
ANSWER :
(B) $\frac{11}{36}$
PROBLEM 13 :
Along the route of a bicycle race, 7 water stations are evenly spaced between the start and finish lines, as shown in the figure below. There are also 2 repair stations evenly spaced between the start and finish lines. The 3 rd water station is located 2 miles after the 1 st repair station. How long is the race in miles?
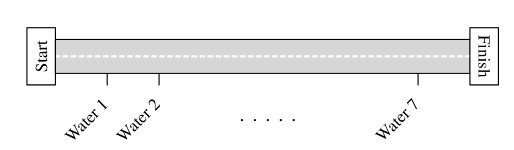
(A) 8
(B) 16
(C) 24
(D) 48
(E) 96
ANSWER :
(D) 48
PROBLEM 14 :
Nicolas is planning to send a package to his friend Anton, who is a stamp collector. To pay for the postage, Nicolas would like to cover the package with a large number of stamps. Suppose he has a collection of 5 -cent, 10 -cent, and 25 -cent stamps, with exactly 20 of each type. What is the greatest number of stamps Nicolas can use to make exactly $\$ 7.10$ in postage? (Note: The amount $\$ 7.10$ corresponds to 7 dollars and 10 cents. One dollar is worth 100 cents.)
(A) 45
(B) 46
(C) 51
(D) 54
(E) 55
ANSWER :
(E) 55
PROBLEM 15 :
Viswam walks half a mile to get to school each day. His route consists of 10 city blocks of equal length and he takes 1 minute to walk each block. Today, after walking 5 blocks, Viswam discovers he has to make a detour, walking 3 blocks of equal length instead of 1 block to reach the next corner. From the time he starts his detour, at what speed, in mph, must he walk, in order to get to school at his usual time? Here's a hint… if you aren't correct, think about using conversions, maybe that's why you're wrong! -RyanZ4552

(A) 4
(B) 4.2
(C) 4.5
(D) 4.8
(E) 5
ANSWER :
(B) 4.2
PROBLEM 16 :
The letters $\mathrm{P}, \mathrm{Q}$, and R are entered into a $20 \times 20$ table according to the pattern shown below. How many Ps, Qs, and Rs will appear in the completed table?
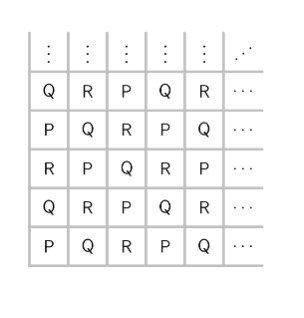
(A) 132 Ps, $134 \mathrm{Qs}, 134 \mathrm{Rs}$
(B) $133 \mathrm{Ps}, 133 \mathrm{Qs}, 134 \mathrm{Rs}$
(C) $133 \mathrm{Ps}, 134 \mathrm{Qs}, 133 \mathrm{Rs}$
(D) $134 \mathrm{Ps}, 132 \mathrm{Qs}, 134 \mathrm{Rs}$
(E) $134 \mathrm{Ps}, 133 \mathrm{Qs}, 133 \mathrm{Rs}$
ANSWER :
(C) $133 \mathrm{Ps}, 134 \mathrm{Qs}, 133 \mathrm{Rs}$
PROBLEM 17 :
A regular octahedron has eight equilateral triangle faces with four faces meeting at each vertex. Jun will make the regular octahedron shown on the right by folding the piece of paper shown on the left. Which numbered face will end up to the right of $Q$ ?
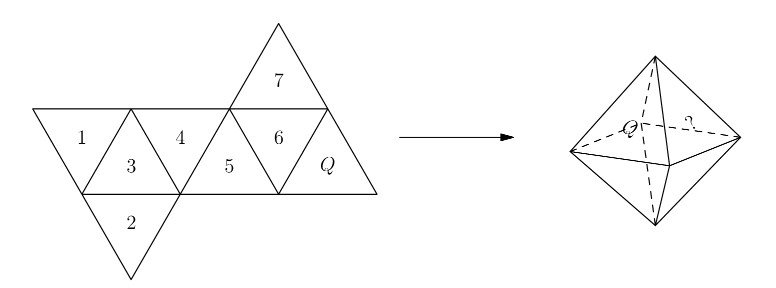
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
ANSWER :
(A) 1
PROBLEM 18 :
Greta Grasshopper sits on a long line of lily pads in a pond. From any lily pad, Greta can jump 5 pads to the right or 3 pads to the left. What is the fewest number of jumps Greta must make to reach the lily pad located 2023 pads to the right of her starting position?
(A) 405
(B) 407
(C) 409
(D) 411
(E) 413
ANSWER :
(D) 411
PROBLEM 19 :
An equilateral triangle is placed inside a larger equilateral triangle so that the region between them can be divided into three congruent trapezoids, as shown below. The side length of the inner triangle is $\frac{2}{3}$ the side length of the larger triangle. What is the ratio of the area of one trapezoid to the area of the inner triangle?
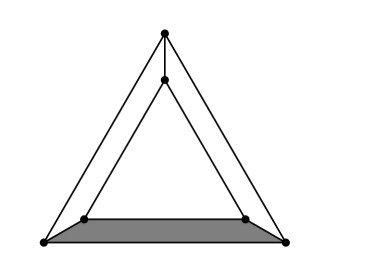
(A) $1: 3$
(B) $3: 8$
(C) $5: 12$
(D) $7: 16$
(E) $4: 9$
ANSWER :
(C) $5: 12$
PROBLEM 20 :
Two integers are inserted into the list $3,3,8,11,28$ to double its range. The mode and median remain unchanged. What is the maximum possible sum of the two additional numbers?
(A) 56
(B) 57
(C) 58
(D) 60
(E) 61
ANSWER :
(D) 60
PROBLEM 21 :
Alina writes the numbers $1,2, \ldots, 9$ on separate cards, one number per card. She wishes to divide the cards into 3 groups of 3 cards so that the sum of the numbers in each group will be the same. In how many ways can this be done?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
ANSWER :
(C) 2
PROBLEM 22 :
In a sequence of positive integers, each term after the second is the product of the previous two terms. The sixth term is 4000 . What is the first term?
(A) 1
(B) 2
(C) 4
(D) 5
(E) 10
ANSWER :
(D) 5
PROBLEM 23 :
Each square in a $3 \times 3$ grid is randomly filled with one of the 4 gray and white tiles shown below on the right.
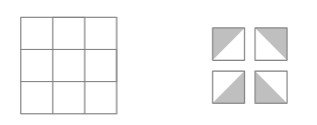
What is the probability that the tiling will contain a large gray diamond in one of the smaller $2 \times 2$ grids? Below is an example of such tiling.
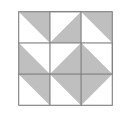
(A) $\frac{1}{1024}$
(B) $\frac{1}{256}$
(C) $\frac{1}{64}$
(D) $\frac{1}{16}$
(E) $\frac{1}{4}$
ANSWER :
(C) $\frac{1}{64}$
PROBLEM 24 :
Isosceles $\triangle A B C$ has equal side lengths $A B$ and $B C$. In the figure below, segments are drawn parallel to $\overline{A C}$ so that the shaded portions of $\triangle A B C$ have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height of $h$ of $\triangle A B C$ ? (Diagram not drawn to scale.)
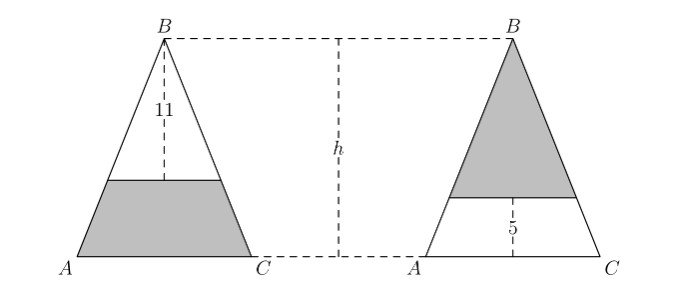
(A) 14.6
(B) 14.8
(C) 15
(D) 15.2
(E) 15.4
ANSWER :
(A) 14.6
PROBLEM 25 :
Fifteen integers $a_1, a_2, a_3, \ldots, a_{15}$ are arranged in order on a number line. The integers are equally spaced and have the property that
$$
1 \leq a_1 \leq 10,13 \leq a_2 \leq 20, \text { and } 241 \leq a_{15} \leq 250 .
$$
What is the sum of digits of $a_{14}$ ?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
SOLUTION :
(A) 8