Problem 1
At Euclid High School, the mathematics teachers are Mrs. Germain, Mr. Newton, and Mrs. Young. There are 11 students in Mrs. Germain's class, 8 in Mr. Newton, and 9 in Mrs. Young's class are taking the AMC 8 this year. How many mathematics students at Euclid High School are taking the contest?
(A) 26
(B) 27
(C) 28
(D) 29
(E) 30
Answer:
(C) 28
Problem 2
If $a @ b=\frac{a \times b}{a+b}$, for $a, b$ positive integers, then what is $5 @ 10$ ?
(A) $\frac{3}{10}$
(B) 1
(C) 2
(D) $\frac{10}{3}$
(E) 50
Answer:
(D) $\frac{10}{3}$
Problem 3
3 The graph shows the price of five gallons of gasoline during the first ten months of the year. By what percent is the highest price more than the lowest price?
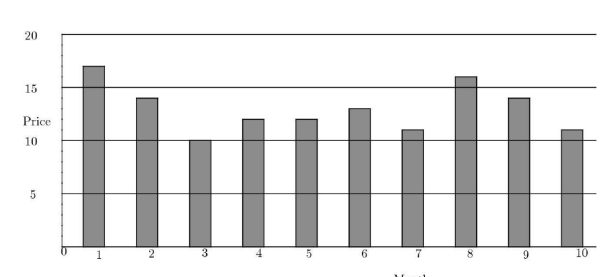
(A) 50
(B) 62
(C) 70
(D) 89
(E) 100
Answer:
(C) 70
Problem 4
What is the sum of the mean, median, and mode of the numbers, $2,3,0,3,1,4,0,3$ ?
(A) 6.5
(B) 7
(C) 7.5
(D) 8.5
(E) 9
Answer:
(C) 7.5
Problem 5
Alice needs to replace a light bulb located 10 centimeters below the ceiling of her kitchen. The ceiling is 2.4 meters above the floor. Alice is 1.5 meters tall and can reach 46 centimeters above her head. Standing on a stool, she can just reach the light bulb. What is the height of the stool, in centimeters?
(A) 32
(B) 34
(C) 36
(D) 38
(E) 40
Answer:
(B) 34
Problem 6
Which of the following has the greatest number of line of symmetry?
(A) Equilateral Triangle (B) Non-square rhombus (C) Non-square rectangle (D) Isosceles Triangle (E) Square
Answer:
(E) Square
Problem 7
Using only pennies, nickels, dimes, and quarters, what is the smallest number of coins Freddie would need so he could pay any amount of money less than one dollar?
(A) 6
(B) 10
(C) 15
(D) 25
(E) 99
Answer:
(B) 10
Problem 8
As Emily is riding her bike on a long straight road, she spots Ermenson skating in the same direction $1 / 2$ mile in front of her. After she passes him, she can see him in her rear mirror until he is $1 / 2$ mile behind her. Emily rides at a constant rate of 12 miles per hour. Ermenson skates at a constant rate of 8 miles per hour. For how many minutes can Emily see Ermenson?
(A) 6
(B) 8
(C) 12
(D) 15
(E) 16
Answer:
(D) 15
Problem 9
Ryan got $80 \%$ of the problems on a 25 -problem test, $90 \%$ on a 40 -problem test, and $70 \%$ on a 10 -problem test. What percent of all problems did Ryan answer correctly?
(A) 64
(B) 75
(C) 80
(D) 84
(E) 86
Answer:
(D) 84
Problem 10
6 pepperoni circles will exactly fit across the diameter of a 12 -inch pizza when placed. If a total of 24 circles of pepperoni are placed on this pizza without overlap, what fraction of the pizza is covered with pepperoni?
(A) $\frac{1}{2}$
(B) $\frac{2}{3}$
(C) $\frac{3}{4}$
(D) $\frac{5}{6}$
(E) $\frac{7}{8}$
Answer:
(B) $\frac{2}{3}$
Problem 11
The top of one tree is 16 feet higher than the top of another tree. The height of the 2 trees are at a ratio of $3: 4$. In feet, how tall is the taller tree?
(A) 48
(B) 64
(C) 80
(D) 96
(E) 112
Answer:
(B) 64
Problem 12
12 & Of the 500 balls in a large bag, $80 \%$ are red and the rest are blue. How many of the red balls must be removed so that $75 \%$ of the remaining balls are red?
(A) 25
(B) 50
(C) 75
(D) 100
(E) 150
Answer:
(D) 100
Problem 13
The lengths of the sides of a triangle in inches are three consecutive integers. The length of the shorter side is $30 \%$ of the perimeter. What is the length of the longest side?
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11
Answer:
(E) 11
Problem 14
What is the sum of the prime factors of 2010 ?
(A) 67
(B) 75
(C) 77
(D) 201
(E) 210
Answer:
(C) 77
Problem 15
A jar contains 5 different colors of gumdrops. $30 \%$ are blue, $20 \%$ are brown, $15 \%$ red, $10 \%$ yellow, and the other 30 gumdrops are green. If half of the blue gumdrops are replaced with brown gumdrops, how many gumdrops will be brown?
(A) 35
(B) 36
(C) 42
(D) 48
(E) 64
Answer:
(C) 42
Problem 16
A square and a circle have the same area. What is the ratio of the side length of the square to the radius of the circle?
(B) $\sqrt{\pi}$
(C) $\pi$
(D) $2 \pi$
(E) $\pi^{2}$
Answer:
(B) $\sqrt{\pi}$
Problem 17
The diagram shows an octagon consisting of 10 unit squares. The portion below $\overline{P Q}$ is a unit square and a triangle with base 5 . If $\overline{P Q}$ bisects the area of the octagon, what is the ratio $\frac{X Q}{Q Y}$ ?
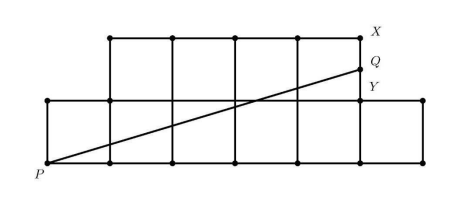
(A) $\frac{2}{5}$
(B) $\frac{1}{2}$
(C) $\frac{3}{5}$
(D) $\frac{2}{3}$
(E) $\frac{3}{4}$
Answer:
(D) $\frac{2}{3}$
Problem 18
A decorative window is made up of a rectangle with semicircles at either end. The ratio of $A D$ to $A B$ is $3: 2$. And $A B$ is 30 inches. What is the ratio of the area of the rectangle to the combined area of the semicircle.
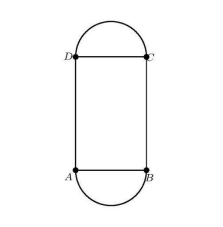
(A) $2: 3$
(B) $3: 2$
(C) $6: \pi$
(D) $9: \pi$
(E) $30: \pi$
Answer:
(C) $6: \pi$
Problem 19
The two circles pictured have the same center $C$. Chord $\overline{A D}$ is tangent to the inner circle at $B, A C$ is 10 , and chord $\overline{A D}$ has length 16 . What is the area between the two circles?
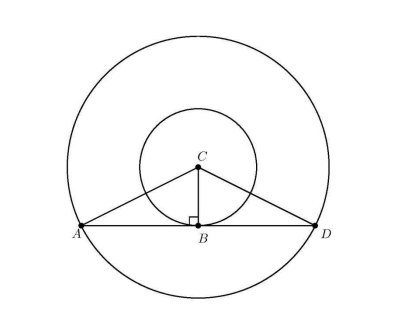
(A) $36 \pi$
(B) $49 \pi$
(C) $64 \pi$
(D) $81 \pi$
(E) $100 \pi$
Answer:
(C) $64 \pi$
Problem 20
In a room, $2 / 5$ of the people are wearing gloves, and $3 / 4$ of the people are wearing hats. What is the minimum number of people in the room wearing both a hat and a glove?
(A) 3
(B) 5
(C) 8
(D) 15
(E) 20
Answer:
(A) 3
Problem 21
Hui is an avid reader. She bought a copy of the best seller Math is Beautiful. On the first day, she read $1 / 5$ of the pages plus 12 more, and on the second day she read $1 / 4$ of the remaining pages plus 15 more. On the third day she read $1 / 3$ of the remaining pages plus 18 more. She then realizes she has 62 pages left, which she finishes the next day. How many pages are in this book?
(A) 120
(B) 180
(C) 240
(D) 300
(E) 360
Answer:
(C) 240
Problem 22
The hundreds digit of a three-digit number is 2 more than the units digit. The digits of the three-digit number are reversed, and the result is subtracted from the original three-digit number. What is the units digit of the result?
(A) 0
(B) 2
(C) 4
(D) 6
(E) 8
Answer:
(E) 8
Problem 23
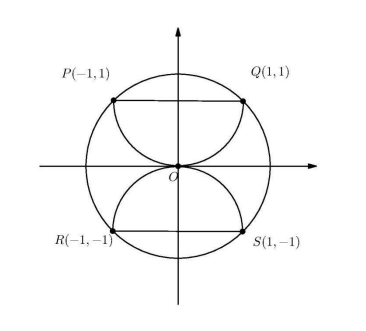
Semicircles $P O Q$ and $R O S$ pass through the center of circle $O$. What is the ratio of the combined areas of the two semicircles to the area of circle $O$ ?
(A) $\frac{\sqrt{2}}{4}$
(B) $\frac{1}{2}$
(C) $\frac{2}{\pi}$
(D) $\frac{2}{3}$
(E) $\frac{\sqrt{2}}{2}$
Answer:
(B) $\frac{1}{2}$
Problem 24
What is the correct ordering of the three numbers, $10^{8}, 5^{12}$, and $2^{24}$ ?
(A) $2^{24}<10^{8}<5^{12}$
(B) $2^{24}<5^{12}<10^{8}$
(C) $5^{12}<2^{24}<10^{8}$ (D) $10^{8}< 5^{12}<2^{24}$ (E) $10^{8}<2^{24}<5^{12}$
Answer:
(A) $2^{24}<10^{8}<5^{12}$
Problem 25
Everyday at school, Jo climbs a flight of 6 stairs. Joe can take the stairs 1,2, or 3 at a time. For example, Jo could climb 3, then 1 , then 2 . In how many ways can Jo climb the stairs?
(A) 13
(B) 18
(C) 20
(D) 22
(E) 24
Answer:
(E) 24