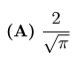QUESTION 1 :
Connie multiplies a number by 2 and gets 60 as her answer. However, she should have divided the number by 2 to get the correct answer. What is the correct answer?
(A) 7.5
(B) 15
(C) 30
(D) 120
(E) 240
ANSWER 1 :
(B) 15
QUESTION 2 :
Karl bought five folders from Pay-A-Lot at a cost of $\$ 2.50$ each. Pay-A-Lot had a $20 \%$-off sale the following day. How much could Karl have saved on the purchase by waiting a day?
(A) $\$ 1.00$
(B) $\$ 2.00$
(C) $\$ 2.50$
(D) $\$ 2.75$
(E) $\$ 5.00$
ANSWER 2 :
(C) $\$ 2.50$
QUESTION 3 :
What is the minimum number of small squares that must be colored black so that a line of symmetry lies on the diagonal $\overline{B D}$ of square $A B C D$ ?
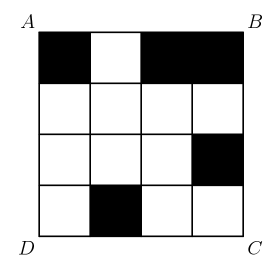
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
ANSWER 3 :
(D) 4
QUESTION 4 :
A square and a triangle have equal perimeters. The lengths of the three sides of the triangle are $6.1 \mathrm{~cm}, 8.2 \mathrm{~cm}$ and 9.7 cm . What is the area of the square in square centimeters?
(A) 24
(B) 25
(C) 36
(D) 48
(E) 64
ANSWER 4 :
(C) 36
QUESTION 5 :
Soda is sold in packs of 6,12 and 24 cans. What is the minimum number of packs needed to buy exactly 90 cans of soda?
(A) 4
(B) 5
(C) 6
(D) 8
(E) 15
ANSWER 5 :
(B) 5
QUESTION 6:
Suppose $d$ is a digit. For how many values of $d$ is $2.00 d 5>2.005 ?$
(A) 0
(B) 4
(C) 5
(D) 6
(E) 10
ANSWER 6 :
(C) 5
QUESTION 7 :
Bill walks $\frac{1}{2}$ mile south, then $\frac{3}{4}$ mile east, and finally $\frac{1}{2}$ mile south. How many miles is he, in a direct line, from his starting point?
(A) 1
(B) $1 \frac{1}{4}$
(C) $1 \frac{1}{2}$
(D) $1 \frac{3}{4}$
(E) 2
ANSWER 7 :
(B) $1 \frac{1}{4}$
QUESTION 8 :
Suppose $m$ and $n$ are positive odd integers. Which of the following must also be an odd integer?
(A) $m+3 n$
(B) $3 m-n$
(C) $3 m^2+3 n^2$
(D) $(n m+3)^2$
(E) $3 m n$
ANSWER 8 :
(E) $3 m n$
QUESTION 9 :
In quadrilateral $A B C D$, sides $\overline{A B}$ and $\overline{B C}$ both have length 10 , sides $\overline{C D}$ and $\overline{D A}$ both have length 17 , and the measure of angle $A D C$ is $60^{\circ}$. What is the length of diagonal $\overline{A C}$ ?
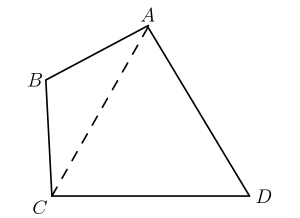
(A) 13.5
(B) 14
(C) 15.5
(D) 17
(E) 18.5
ANSWER 9 :
(D) 17
QUESTION 10 :
Joe had walked half way from home to school when he realized he was late. He ran the rest of the way to school. He ran 3 times as fast as he walked. Joe took 6 minutes to walk half way to school. How many minutes did it take Joe to get from home to school?
(A) 7
(B) 7.3
(C) 7.7
(D) 8
(E) 8.3
ANSWER 10 :
(D) 8
QUESTION 11 :
The sales tax rate in Rubenenkoville is $6 \%$. During a sale at the Bergville Coat Closet, the price of a coat is discounted $20 \%$ from its $\$ 90.00$ price. Two clerks, Jack and Jill, calculate the bill independently. Jack rings up $\$ 90.00$ and adds $6 \%$ sales tax, then subtracts $20 \%$ from this total. Jill rings up $\$ 90.00$, subtracts $20 \%$ of the price, then adds $6 \%$ of the discounted price for sales tax. What is Jack's total minus Jill's total?
(A) $-\$ 1.06$
(B) $-\$ 0.53$
(C) $\$ 0$
(D) $\$ 0.53$
(E) $\$ 1.06$
ANSWER 11 :
(C) $\$ 0$
QUESTION 12 :
Big AI, the ape, ate 100 bananas from May 1 through May 5. Each day he ate six more bananas than on the previous day. How many bananas did Big Al eat on May 5?
(A) 20
(B) 22
(C) 30
(D) 32
(E) 34
ANSWER 12 :
(D) 32
QUESTION 13 :
The area of polygon $A B C D E F$ is 52 with $A B=8, B C=9$ and $F A=5$. What is $D E+E F$ ?
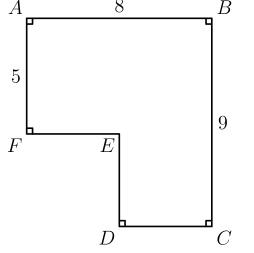
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11
ANSWER 13 :
(C) 9
QUESTION 14 :
The Little Twelve Basketball Conference has two divisions, with six teams in each division. Each team plays each of the other teams in its own division twice and every team in the other division once. How many conference games are scheduled?
(A) 80
(B) 96
(C) 100
(D) 108
(E) 192
ANSWER 14 :
(B) 96
QUESTION 15 :
How many different isosceles triangles have integer side lengths and perimeter $23 ?$
(A) 2
(B) 4
(C) 6
(D) 9
(E) 11
ANSWER 15 :
(C) 6
QUESTION 16 :
A five-legged Martian has a drawer full of socks, each of which is red, white or blue, and there are at least five socks of each color. The Martian pulls out one sock at a time without looking. How many socks must the Martian remove from the drawer to be certain there will be 5 socks of the same color?
(A) 6
(B) 9
(C) 12
(D) 13
(E) 15
ANSWER 16 :
(D) 13
QUESTION 17 :
The results of a cross-country team's training run are graphed below. Which student has the greatest average speed?
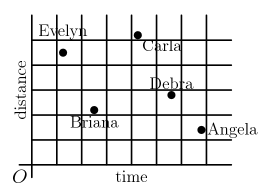
(A) Angela
(B) Briana
(C) Carla
(D) Debra
(E) Evelyn
ANSWER 17 :
(E) Evelyn
QUESTION 18 :
How many three-digit numbers are divisible by 13 ?
(A) 7
(B) 67
(C) 69
(D) 76
(E) 77
ANSWER 18 :
(C) 69
QUESTION 19 :
What is the perimeter of trapezoid $A B C D$ ?
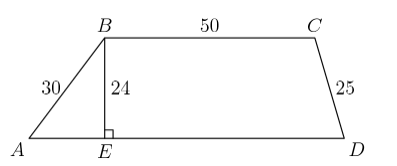
(A) 180
(B) 188
(C) 196
(D) 200
(E) 204
ANSWER 19 :
(A) 180
QUESTION 20 :
Alice and Bob play a game involving a circle whose circumference is divided by 12 equally-spaced points. The points are numbered clockwise, from 1 to 12 . Both start on point 12 . Alice moves clockwise and Bob, counterclockwise. In a turn of the game, Alice moves 5 points clockwise and Bob moves 9 points counterclockwise. The game ends when they stop on the same point. How many turns will this take?
(A) 6
(B) 8
(C) 12
(D) 14
(E) 24
ANSWER 20 :
(A) 6
QUESTION 21 :
How many distinct triangles can be drawn using three of the dots below as vertices?

(A) 9
(B) 12
(C) 18
(D) 20
(E) 24
ANSWER 21 :
(C) 18
QUESTION 22 :
A company sells detergent in three different sized boxes: small (S), medium (M) and large (L). The medium size costs 50\% more than the small size and contains $20 \%$ less detergent than the large size. The large size contains twice as much detergent as the small size and costs $30 \%$ more than the medium size. Rank the three sizes from best to worst buy.
(A) $S M L$
(B) $L M S$
(C) $M S L$
(D) $L S M$
(E) $M L S$
ANSWER 22 :
(E) $M L S$
QUESTION 23 :
Isosceles right triangle $A B C$ encloses a semicircle of area $2 \pi$. The circle has its center $O$ on hypotenuse $\overline{A B}$ and is tangent to sides $\overline{A C}$ and $\overline{B C}$. What is the area of triangle $A B C$ ?
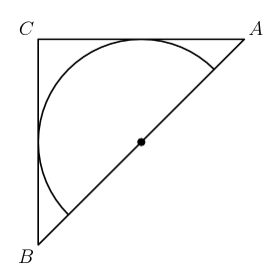
(A) 6
(B) 8
(C) $3 \pi$
(D) 10
(E) $4 \pi$
ANSWER 23 :
(B) 8
QUESTION 24 :
A certain calculator has only two keys $[+1]$ and $[\mathrm{x} 2]$. When you press one of the keys, the calculator automatically displays the result. For instance, if the calculator originally displayed " 9 " and you pressed [ +1 ], it would display " 10 ." If you then pressed [ $x 2$ ], it would display " 20 ." Starting with the display "1," what is the fewest number of keystrokes you would need to reach "200"?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
ANSWER 24 :
(B) 9
QUESTION 25 :
A square with side length 2 and a circle share the same center. The total area of the regions that are inside the circle and outside the square is equal to the total area of the regions that are outside the circle and inside the square. What is the radius of the circle?
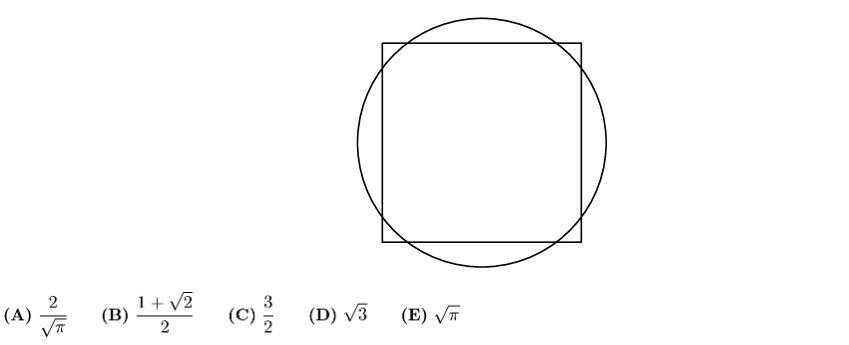
ANSWER 25 :