Problem 1
Margie bought 3 apples at a cost of 50 cents each. She paid with a 5 -dollar bill. How much change did Margie receive?
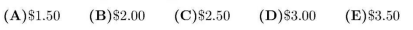
Answer:
(E) Is the correct answer.
Problem 2
Karl's rectangular vegetable garden is 20 by 45 feet, and Makenna's is 25 by 40 feet. Which garden is larger in area?
(A) Karl's garden is larger by 100 square feet.
(B) Karl's garden is larger by 25 square feet.
(C) The gardens are the same size.
(D) Makenna's garden is larger by 25 square feet.
(E) Makenna's garden is larger by 100 square feet.
Answer:
(E) Makenna's garden is larger by 100 square feet.
Problem 3
Extend the square pattern of 8 black and 17 white square tiles by attaching a border of black tiles around the square. What is the ratio of black tiles to white tiles in the extended pattern?
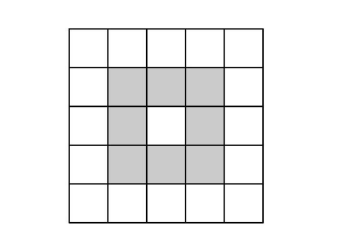

Answer:
(D) Is the correct answer.
Problem 4
Here is a list of the numbers of fish that Tyler caught in nine outings last summer:
Which statement about the mean, median, and mode is true?


Answer:
(C) Is the correct answer.
Problem 5
What time was it 2011 minutes after midnight on January 1, 2011?
(A)January 1 at 9:31PM
(B)January 1 at 11:51PM
(C)January 2 at 3:11AM
(D)January 2 at 9:31AM
(E)January 2 at 6:01PM
Answer:
(D)January 2 at 9:31AM
Problem 6
In a town of 351 adults, every adult owns a car, motorcycle, or both. If 331 adults own cars and 45 adults own motorcycles, how many of the car owners do not own a motorcycle?
(A) 20
(B) 25
(C) 45
(D)306
(E)351
Answer:
(D)306
Problem 7
Each of the following four large congruent squares is subdivided into combinations of congruent triangles or rectangles and is partially bolded. What percent of the total area is partially bolded?
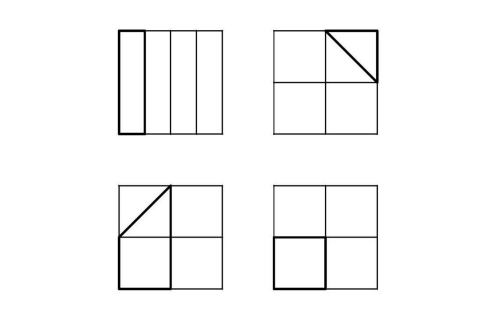
Answer:
(C) Is the correct answer.
Problem 8
Bag A has three chips labeled 1, 3, and 5. Bag B has three chips labeled 2, 4 , and 6 . If one chip is drawn from each bag, how many different values are possible for the sum of the two numbers on the chips?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 9
Answer:
(B) 5
Problem 9
Carmen takes a long bike ride on a hilly highway. The graph indicates the miles traveled during the time of her ride. What is Carmen's average speed for her entire ride in miles per hour?
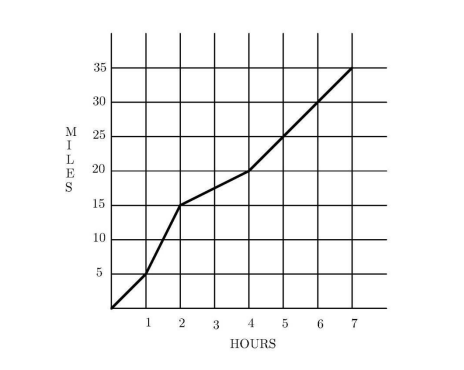
(A) 2
(B) 2.5
(C) 4
(D) 4.5
(E) 5
Answer:
(E) 5
Problem 10
The taxi fare in Gotham City is $\$ 2.40$ for the first $\frac{1}{2}$ mile and additional mileage charged at the rate $\$ 0.20$ for each additional 0.1 mile. You plan to give the driver a $\$ 2$ tip. How many miles can you ride for $\$ 10$ ?
(A) 3.0
(B) 3.25
(C) 3.3
(D) 3.5
(E) 3.75
Answer:
(C) 3.3
Problem 11
The graph shows the number of minutes studied by both Asha (black bar) and Sasha (grey bar) in one week. On the average, how many more minutes per day did Sasha study than Asha?
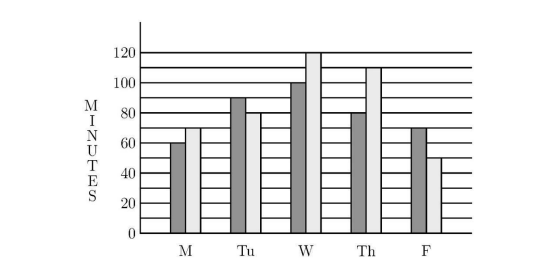
(A) 6
(B) 8
(C) 9
(D) 10
(E) 12
Answer:
(A) 6
Problem 12
Angie, Bridget, Carlos, and Diego are seated at random around a square table, one person to a side. What is the probability that Angie and Carlos are seated opposite each other?
Answer:
(B) Is the correct answer.
Problem 13
Two congruent squares, $A B C D$ and $P Q R S$, have side length 15. They overlap to form the 15 by 25 rectangle $A Q R D$ shown. What percent of the area of rectangle $A Q R D$ is shaded?
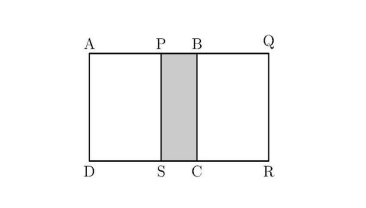
(A) 15
(B) 18
(C) 20
(D) 24
(E) 25
Answer:
(C) 20
Problem 14
There are 270 students at Colfax Middle School, where the ratio of boys to girls is $5: 4$. There are 180 students at Winthrop Middle School, where the ratio of boys to girls is $4: 5$. The two schools hold a dance and all students from both schools attend. What fraction of the students at the dance are girls?
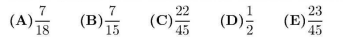
Answer:
(C) Is the correct answer.
Problem 15
How many digits are in the product $4^{5} \cdot 5^{10}$ ?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
Answer:
(D) 11
Problem 16
Let $A$ be the area of the triangle with sides of length 25,25 , and 30 . Let $B$ be the area of the triangle with sides of length 25,25 , and 40 . What is the relationship between $A$ and $B$ ?
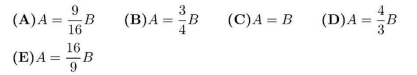
Answer:
(C) Is the corret answer.
Problem 17
Let $w, x, y$, and $z$ be whole numbers. If $2^{w} \cdot 3^{x} \cdot 5^{y} \cdot 7^{z}=588$, then what does $2 w+3 x+5 y+7 z$ equal?
(A) 21
(B) 25
(C) 27
(D) 35
(E) 56
Answer:
(A) 21
Problem 18
A fair 6 -sided die is rolled twice. What is the probability that the first number that comes up is greater than or equal to the second number?
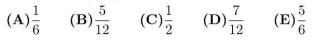
Answer:
(D) Is the correct answer.
Problem 19
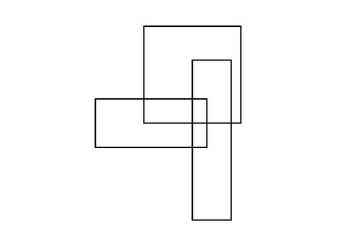
How many rectangles are in this figure?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
Answer:
(D) 11
Problem 20
Quadrilateral $A B C D$ is a trapezoid, $A D=15, A B=50, B C=20$, and the altitude is 12 . What is the area of the trapeziod?
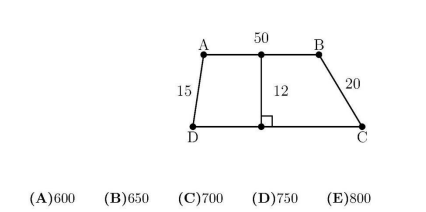
Answer:
(D) Is the correct answer.
Problem 21
Students guess that Norb's age is $24,28,30,32,36,38,41,44,47$, and 49 . Norb says, "At least half of you guessed too low, two of you are off by one, and my age is a prime number." How old is Norb?
(A) 29
(B)31
(C) 37
(D)43
(E) 48
Answer:
(C) 37
Problem 22
22 What is the tens digit of $7^{2011}$ ?
(A) 0
(B) 1
(C) 3
(D) 4
(E) 7
Answer:
(D) 4
Problem 23
How many 4-digit positive integers have four different digits, where the leading digit is not zero, the integer is a multiple of 5 , and 5 is the largest digit?
(A) 24
(B) 48
(C) 60
(D) 84
(E) 108
Answer:
(D) 84
Problem 24
In how many ways can 10001 be written as the sum of two primes?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Answer:
(A) 0
Problem 25
A circle with radius 1 is inscribed in a square and circumscribed about another square as shown. Which fraction is closest to the ratio of the circle's shaded area to the area between the two squares?
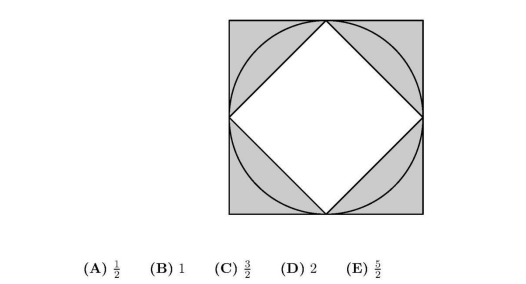
Answer:
(A) Is the correct answer.