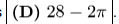QUESTION 1 :
On a map, a 12 -centimeter length represents 72 kilometers. How many kilometers does a 17 -centimeter length represent?
(A) 6
(B) 102
(C) 204
(D) 864
(E) 1224
ANSWER 1 :
(B) 102
QUESTION 2 :
How many different four-digit numbers can be formed by rearranging the four digits in 2004 ?
(A) 4
(B) 6
(C) 16
(D) 24
(E) 81
ANSWER 2 :
(B) 6
QUESTION 3 :
Twelve friends met for dinner at Oscar's Overstuffed Oyster House, and each ordered one meal. The portions were so large, there was enough food for 18 people. If they share, how many meals should they have ordered to have just enough food for the 12 of them?
(A) 8
(B) 9
(C) 10
(D) 15
(E) 18
ANSWER 3 :
(A) 8
QUESTION 4 :
Ms. Hamilton's eighth-grade class wants to participate in the annual three-person-team basketball tournament. Lance, Sally, Joy, and Fred are chosen for the team. In how many ways can the three starters be chosen?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
ANSWER 4 :
(B) 4
QUESTION 5 :
Ms. Hamilton's eighth-grade class wants to participate in the annual three-person-team basketball tournament. The losing team of each game is eliminated from the tournament. If sixteen teams compete, how many games will be played to determine the winner?
(A) 4
(B) 7
(C) 8
(D) 15
(E) 16
ANSWER 5 :
(D) 15
QUESTION 6 :
After Sally takes 20 shots, she has made $55 \%$ of her shots. After she takes 5 more shots, she raises her percentage to $56 \%$. How many of the last 5 shots did she make?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
ANSWER 6:
(C) 3
QUESTION 7 :
An athlete's target heart rate, in beats per minute, is $80 \%$ of the theoretical maximum heart rate. The maximum heart rate is found by subtracting the athlete's age, in years, from 220 . To the nearest whole number, what is the target heart rate of an athlete
who is 26 years old?
(A) 134
(B) 155
(C) 176
(D) 194
(E) 243
ANSWER 7:
(B) 155
QUESTION 8 :
Find the number of two-digit positive integers whose digits total 7.
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
ANSWER 8 :
(B) 7
QUESTION 9 :
The average of the five numbers in a list is 54 . The average of the first two numbers is 48 . What is the average of the last three numbers?
(A) 55
(B) 56
(C) 57
(D) 58
(E) 59
ANSWER 9 :
(D) 58
QUESTION 10 :
Handy Aaron helped a neighbor $1 \frac{1}{4}$ hours on Monday, 50 minutes on Tuesday, from 8:20 to 10:45 on Wednesday morning, and a half-hour on Friday. He is paid $\$ 3$ per hour. How much did he earn for the week?
(A) $\$ 8$
(B) $\$ 9$
(C) $\$ 10$
(D) $\$ 12$
(E) $\$ 15$
ANSWER 10:
(E) $\$ 15$
QUESTION 11:
The numbers $-2,4,6,9$ and 12 are rearranged according to these rules:
What is the average of the first and last numbers?
(A) 3.5
(B) 5
(C) 6.5
(D) 7.5
(E) 8
ANSWER 11 :
(C) 6.5
QUESTION 12 :
Niki usually leaves her cell phone on. If her cell phone is on but she is not actually using it, the battery will last for 24 hours. If she is using it constantly, the battery will last for only 3 hours. Since the last recharge, her phone has been on 9 hours, and during
that time she has used it for 60 minutes. If she doesn't talk any more but leaves the phone on, how many more hours will the battery last?
(A) 7
(B) 8
(C) 11
(D) 14
(E) 15
ANSWER 12 :
(B) 8
QUESTION 13 :
Amy, Bill and Celine are friends with different ages. Exactly one of the following statements is true.
I. Bill is the oldest.
II. Amy is not the oldest.
III. Celine is not the youngest.
Rank the friends from the oldest to the youngest.
(A) Bill, Amy, Celine
(B) Amy, Bill, Celine
(C) Celine, Amy, Bill
(D) Celine, Bill, Amy
(E) Amy, Celine, Bill
ANSWER 13 :
(E) Amy, Celine, Bill
QUESTION 14 :
What is the area enclosed by the geoboard quadrilateral below?
(A) 15
(B) $18 \frac{1}{2}$
(C) $22 \frac{1}{2}$
(D) 27
(E) 41
ANSWER 14:
(C) $22 \frac{1}{2}$
QUESTION 15 :
Thirteen black and six white hexagonal tiles were used to create the figure below. If a new figure is created by attaching a border of white tiles with the same size and shape as the others, what will be the difference between the total number of white tiles and the total number of black tiles in the new figure?

(A) 5
(B) 7
(C) 11
(D) 12
(E) 18
ANSWER 15 :
(C) 11
QUESTION 16 :
Two 600 mL pitchers contain orange juice. One pitcher is $1 / 3$ full and the other pitcher is $2 / 5$ full. Water is added to fill each pitcher completely, then both pitchers are poured into one large container. What fraction of the mixture in the large container is orange juice?
(A) $\frac{1}{8}$
(B) $\frac{3}{16}$
(C) $\frac{11}{30}$
(D) $\frac{11}{19}$
(E) $\frac{11}{15}$
ANSWER 16 :
(C) $\frac{11}{30}$
QUESTION 17 :
Three friends have a total of 6 identical pencils, and each one has at least one pencil. In how many ways can this happen?
(A) 1
(B) 3
(C) 6
(D) 10
(E) 12
ANSWER 17 :
(D) 10
QUESTION 18 :
Five friends compete in a dart-throwing contest. Each one has two darts to throw at the same circular target, and each individual's score is the sum of the scores in the target regions that are hit. The scores for the target regions are the whole numbers 1 through 10 . Each throw hits the target in a region with a different value. The scores are: Alice 16 points, Ben 4 points, Cindy 7 points, Dave 11 points, and Ellen 17 points. Who hits the region worth 6 points?
(A) Alice
(B) Ben
(C) Cindy
(D) Dave
(E) Ellen
ANSWER 18 :
(A) Alice
QUESTION 19 :
A whole number larger than 2 leaves a remainder of 2 when divided by each of the numbers $3,4,5$, and 6 . The smallest such number lies between which two numbers?
(A) 40 and 49
(B) 60 and 79
(C) 100 and 129
(D) 210 and 249
(E) 320 and 369
ANSWER 19 :
(B) 60 and 79
QUESTION 20 :
Two-thirds of the people in a room are seated in three-fourths of the chairs. The rest of the people are standing. If there are 6 empty chairs, how many people are in the room?
(A) 12
(B) 18
(C) 24
(D) 27
(E) 36
ANSWER 20 :
(D) 27
QUESTION 21 :
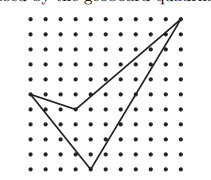
Spinners $A$ and $B$ are spun. On each spinner, the arrow is equally likely to land on each number. What is the probability that the product of the two spinners' numbers is even?
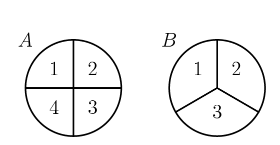
ANSWER 21 :
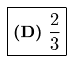
QUESTION 22 :
At a party there are only single women and married men with their wives. The probability that a randomly selected woman is single is $\frac{2}{5}$. What fraction of the people in the room are married men?
(A) $\frac{1}{3}$
(B) $\frac{3}{8}$
(C) $\frac{2}{5}$
(D) $\frac{5}{12}$
(E) $\frac{3}{5}$
ANSWER 22 :
(B) $\frac{3}{8}$
QUESTION 23 :
Tess runs counterclockwise around rectangular block $J K L M$. She lives at corner $J$. Which graph could represent her straight-line distance from home?
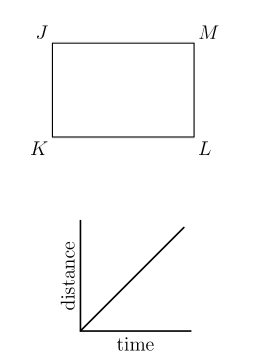
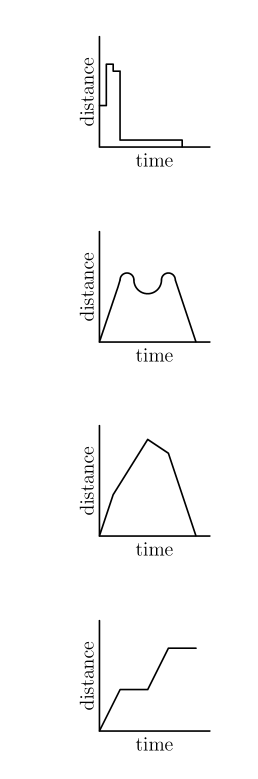
ANSWER 23 :
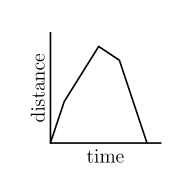
QUESTION 24 :
In the figure, $A B C D$ is a rectangle and $E F G H$ is a parallelogram. Using the measurements given in the figure, what is the length $d$ of the segment that is perpendicular to $\overline{H E}$ and $\overline{F G}$ ?
(A) 6.8
(B) 7.1
(C) 7.6
(D) 7.8
(E) 8.1
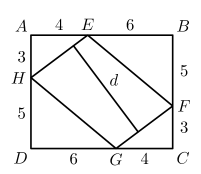
ANSWER 24 :
(C) 7.6
QUESTION 25 :
Two $4 \times 4$ squares intersect at right angles, bisecting their intersecting sides, as shown. The circle's diameter is the segment between the two points of intersection. What is the area of the shaded region created by removing the circle from the squares?
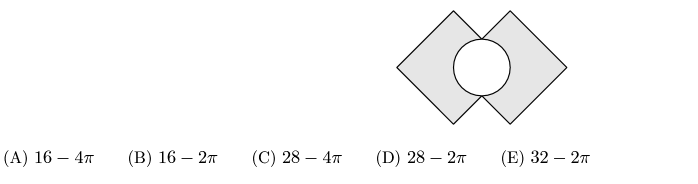
ANSWER 26 :