PROBLEM 1 :
Aunt Anna is 42 years old. Caitlin is 5 years younger than Brianna, and Brianna is half as old as Aunt Anna. How old is Caitlin?
(A) 15
(B) 16
(C) 17
(D) 21
(E) 37
ANSWER : (B) 16
PROBLEM 2 :
Which of these numbers is less than its reciprocal?
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
ANSWER : (A) -2
PROBLEM 3 :
How many whole numbers lie in the interval between $\frac{5}{3}$ and $2 \pi$ ?
(A) 2
(B) 3
(C) 4
(D) 5
(E) infinitely many
ANSWER : (D) 5
PROBLEM 4 :
In 1960 only $5 \%$ of the working adults in Carlin City worked at home. By 1970 the "at-home" work force had increased to $8 \%$. In 1980 there were approximately $15 \%$ working at home, and in 1990 there were $30 \%$. The graph that best illustrates this is:
\end{enumerate}
\begin{figure}[h]
\begin{center}
\captionsetup{labelformat=empty}
\caption{(A)}
\texttt{https://cdn.mathpix.com/cropped/e2a73bec-d083-4216-8a5a-71e828340c7a-2.jpg?height=185&width=267&top_left_y=946&top_left_x=222}
\end{center}
\end{figure}
\begin{figure}[h]
\begin{center}
\texttt{https://cdn.mathpix.com/cropped/e2a73bec-d083-4216-8a5a-71e828340c7a-2.jpg?height=182&width=262&top_left_y=946&top_left_x=657}
\captionsetup{labelformat=empty}
\caption{(B)}
\end{center}
\end{figure}
\texttt{https://cdn.mathpix.com/cropped/e2a73bec-d083-4216-8a5a-71e828340c7a-2.jpg?height=184&width=272&top_left_y=944&top_left_x=1085}
(C)
\begin{figure}[h]
\begin{center}
\captionsetup{labelformat=empty}
\caption{(E)}
\texttt{https://cdn.mathpix.com/cropped/e2a73bec-d083-4216-8a5a-71e828340c7a-2.jpg?height=178&width=263&top_left_y=1195&top_left_x=679}
\end{center}
\end{figure}
(D)
\begin{figure}[h]
\begin{center}
\captionsetup{labelformat=empty}
\caption{(E)}
\includegraphics[max width=\textwidth]{e2a73bec-d083-4216-8a5a-71e828340c7a-2(1)}
\end{center}
\end{figure}
\begin{enumerate}
\setcounter{enumi}{4}
\item
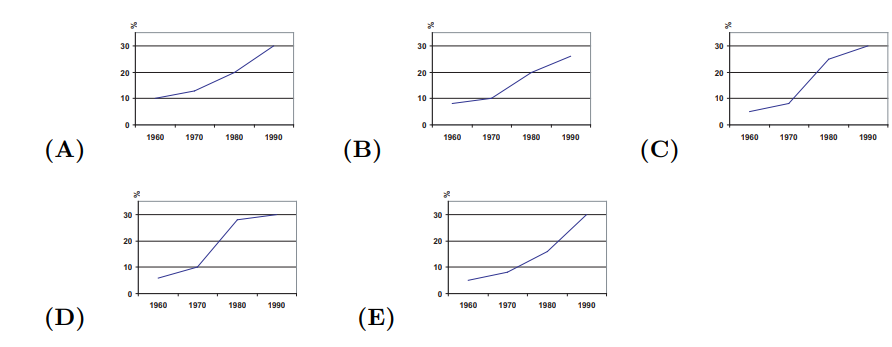
ANSWER : (E)
PROBLEM 5 :
Each principal of Lincoln High School serves exactly one 3 -year term. What is the maximum number of principals this school could have during an 8 -year period?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 8
ANSWER :
PROBLEM 6 :
Figure $A B C D$ is a square. Inside this square three smaller squares are drawn with side lengths as labeled. the area of the shaded L-shaped region is
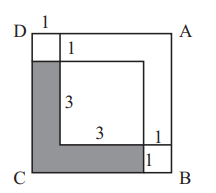
(A) 7
(B) 10
(C) 12.5
(D) 14
(E) 15
ANSWER : (C) 12.5
PROBLEM 7 :
What is the minimum possible product of three different numbers of the set ${-8,-6,-4,0,3,5,7}$ ?
(A) -336
(B) -280
(C) -210
(D) -192
(E) 0
ANSWER : (B) -280
PROBLEM 8 :
Three dice with faces numbered 1 through 6 are stacked as shown. Seven of the eighteen faces are visible, leaving eleven faces hidden(back, bottom, between). The total number of dots NOT visible in this view is
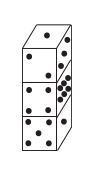
(A) 21
(B) 22
(C) 31
(D) 41
(E) 53
ANSWER : (D) 41
PROBLEM 9 :
Three-digit powers of 2 and 5 are used in this cross-number puzzle. What is the only possible digit for the outlined square?
\end{enumerate}
\section*{ACROSS}
\begin{enumerate}
\setcounter{enumi}{1}
\item $2^{m}$
\end{enumerate}
DOWN
\begin{enumerate}
\item $5^{n}$\
\includegraphics[max width=\textwidth, center]{e2a73bec-d083-4216-8a5a-71e828340c7a-3(1)}\
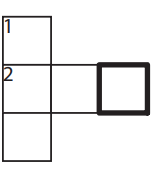
(A) 0
(B) 2
(C) 4
(D) 6
(E) 8
ANSWER : (D)
PROBLEM 10 :
Ara and Shea were once the same height. Since then Shea has grown $20 \%$ while Ara has grown half as many inches as Shea. Shea is now 60 inches tall. How tall, in inches, is Ara now?
(A) 48
(B) 51
(C) 52
(D) 54
(E) 55
ANSWER : (E) 55
PROBLEM 11 :
The number 64 has the property that it is divisible by its units digit. How many whole numbers between 10 and 50 have this property?
(A) 15
(B) 16
(C) 17
(D) 18
(E) 20
ANSWER : (C) 17
PROBLEM 12 :
A block wall 100 feet long and 7 feet high will be constructed using blocks that are 1 foot high and either 2 feet long or 1 foot long (no blocks may be cut). The vertical joins in the\
\texttt{https://cdn.mathpix.com/cropped/e2a73bec-d083-4216-8a5a-71e828340c7a-4.jpg?height=105&width=293&top_left_y=166&top_left_x=1024}\
blocks must be staggered as shown, and the wall must be even on the ends. What is the smallest number of blocks needed to build this wall?
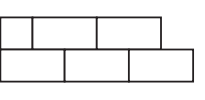
(A) 344
(B) 347
(C) 350
(D) 353
(E) 356
ANSWER : (D) 353
PROBLEM 13 :
In triangle $C A T$, we have $\angle A C T=\angle A T C$ and $\angle C A T=36^{\circ}$. If $\overline{T R}$ bisects $\angle A T C$, then $\angle C R T=$\
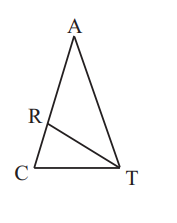
(A) $16^{\circ}$
(B) $51^{\circ}$
(C) $72^{\circ}$
(D) $90^{\circ}$
(E) $108^{\circ}$
ANSWER : (C) $72^{\circ}$
PROBLEM 14 :
What is the units digit of $19^{19}+99^{99}$ ?
(A) 0
(B) 1
(C) 2
(D) 8
(E) 9
ANSWER : (D) 8
PROBLEM 15 :
Triangle $A B C, A D E$, and $E F G$ are all equilateral. Points $D$ and $G$ are midpoints of $\overline{A C}$ and $\overline{A E}$, respectively. If $A B=4$, what is the perimeter of figure $A B C D E F G$ ?
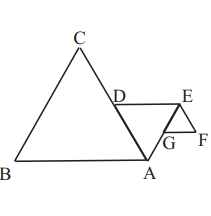
(A) 12
(B) 13
(C) 15
(D) 18
(E) 21
ANSWER : (C) 15
PROBLEM 16 :
In order for Mateen to walk a kilometer $(1000 \mathrm{~m})$ in his rectangular backyard, he must walk the length 25 times or walk its perimeter 10 times. What is the area of Mateen's backyard in square meters?
(A) 40
(B) 200
(C) 400
(D) 500
(E) 1000
ANSWER : (C) 400
PROBLEM 17 :
The operation $\otimes$ is defined for all nonzero numbers by $a \otimes b=\frac{a^{2}}{b}$. Determine $[(1 \otimes 2) \otimes 3]-[1 \otimes(2 \otimes 3)]$.
(A) $-\frac{2}{3}$
(B) $-\frac{1}{4}$
(C) 0\
(D) $\frac{1}{4}$
(E) $\frac{2}{3}$
ANSWER : (A) $-\frac{2}{3}$
PROBLEM 18 :
Consider these two geoboard quadrilaterals. Which of the following statements is true?
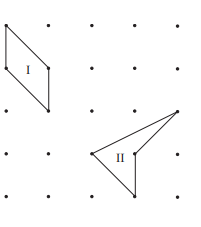
(A) The area of quadrilateral I is more than the area of quadri- • lateral II.
(B) The area of quadrilateral I is less than the area of quadrilateral II.
(C) The quadrilaterals have the same area and the same perimeter.
(D) The quadrilaterals have the same area, but the perimeter of I is more than the perimeter of II.
(E) The quadrilaterals have the same area, but the perimeter of I is less than the perimeter of II.
ANSWER : (E) The quadrilaterals have the same area, but the perimeter of I is less than the perimeter of II.
PROBLEM 19 :
Three circular arcs of radius 5 units bound the region shown. $\operatorname{Arcs} A B$ and $A D$ are quarter-circles, and $\operatorname{arc} B C D$ is a semicircle. What is the area, in square units, of the region?
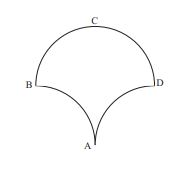
(A) 25
(B) $10+5 \pi$
(C) 50
(D) $50+5 \pi$
\includegraphics[max width=\textwidth, center]{e2a73bec-d083-4216-8a5a-71e828340c7a-5}
(E) $25 \pi$
ANSWER : (C) 50
PROBLEM 20 :
You have nine coins: a collection of pennies, nickels, dimes, and quarters having a total value of $\$ 1.02$, with at least one coin of each type. How many dimes must you have?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
ANSWER : (A) 1
PROBLEM 21 :
Keiko tosses one penny and Ephraim tosses two pennies. The probability that Ephraim gets the same number of heads that Keiko gets is
(A) $\frac{1}{4}$
(B) $\frac{3}{8}$
(C) $\frac{1}{2}$
(D) $\frac{2}{3}$
(E) $\frac{3}{4}$
ANSWER : (B) $\frac{3}{8}$
PROBLEM 22 :
A cube has edge length 2. Suppose that we glue a cube of edge length 1 on top of the big cube so that one of its faces rests entirely on the top face of the larger cube. The percent increase in the surface area (sides, top, and bottom) from the original cube to the new solid formed is closest to:
\texttt{https://cdn.mathpix.com/cropped/e2a73bec-d083-4216-8a5a-71e828340c7a-6.jpg?height=232&width=200&top_left_y=557&top_left_x=1117}
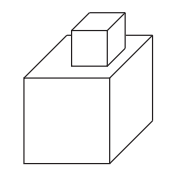
(A) 10
(B) 15
(C) 17
(D) 21
(E) 25
ANSWER : (C) 17
PROBLEM 23 :
There is a list of seven numbers. The average of the first four numbers is 5 , and the average of the last four numbers is 8 . If the average of all seven numbers is $6 \frac{4}{7}$, then the number common to both sets of four numbers is
(A) $5 \frac{3}{7}$
(B) 6
(C) $6 \frac{4}{7}$
(D) 7
(E) $7 \frac{3}{7}$
ANSWER : (B) 6
PROBLEM 24 :
If $\angle A=20^{\circ}$ and $\angle A F G=\angle A G F$, Then $\angle B+\angle D=$
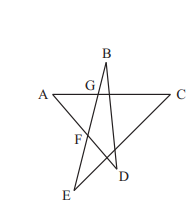
(A) $48^{\circ}$
(B) $60^{\circ}$
(C) $72^{\circ}$
(D) $80^{\circ}$
(E) $90^{\circ}$
ANSWER : (D) $80^{\circ}$
PROBLEM 25 :
The area of rectangle $A B C D$ is 72 . If point $A$ and the midpoints of $\overline{B C}$ and $\overline{C D}$ are joined to form a triangle, the area of that triangle is
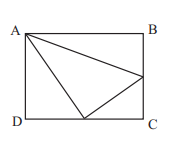
(A) 21
(B) 27
(C) 30
(D) 36
(E) 40
ANSWER : (B) 27
