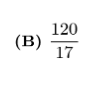Question 1 :
The longest professional tennis match ever played lasted a total of 11 hours and 5 minutes. How many minutes was this?
(A) 605
(B) 655
(C) 665
(D) 1005
(E) 1105
Answer 1 :
(C) 665
Question 2 :
In rectangle $A B C D, A B=6$ and $A D=8$. Point $M$ is the midpoint of $\overline{A D}$. What is the area of $\triangle A M C$ ?
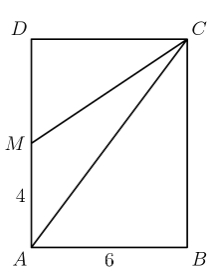
(A) 12
(B) 15
(C) 18
(D) 20
(E) 24
Answer 2 :
(A) 12
Question 3 :
Four students take an exam. Three of their scores are 70,80 , and 90 . If the average of their four scores is 70 , then what is the remaining score?
(A) 40
(B) 50
(C) 55
(D) 60
(E) 70
Answer 3 :
(A) 40
Question 4 :
When Cheenu was a boy, he could run 15 miles in 3 hours and 30 minutes. As an old man, he can now walk 10 miles in 4 hours. How many minutes longer does it take for him to walk a mile now compared to when he was a boy?
(A) 6
(B) 10
(C) 15
(D) 18
(E) 30
Answer 4 :
(B) 10
Question 5 :
The number $N$ is a two-digit number.
What is the remainder when $N$ is divided by 11 ?
(A) 0
(B) 2
(C) 4
(D) 5
(E) 7
Answer 5 :
(E) 7
Question 6 :
The following bar graph represents the length (in letters) of the names of 19 people. What is the median length of these names?
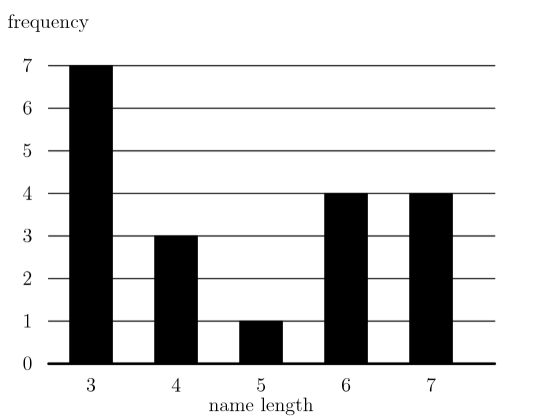
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
Answer 6 :
(B) 4
Question 7 :
Which of the following numbers is not a perfect square?
(A) $1^{2016}$
(B) $2^{2017}$
(C) $3^{2018}$
(D) $4^{2019}$
(E) $5^{2020}$
Answer 7 :
(B) $2^{2017}$
Question 8 :
Find the value of the expression
$$
100-98+96-94+92-90+\cdots+8-6+4-2 .
$$
(A) 20
(B) 40
(C) 50
(D) 80
(E) 100
Answer 8 :
(C) 50
Question 9 :
What is the sum of the distinct prime integer divisors of $2016 ?$
(A) 9
(B) 12
(C) 16
(D) 49
(E) 63
Answer 9 :
(B) 12
Question 10 :
Suppose that $a * b$ means $3 a-b$. What is the value of $x$ if
$$
2 *(5 * x)=1
$$
(A) $\frac{1}{10}$
(B) 2
(C) $\frac{10}{3}$
(D) 10
(E) 14
Answer 10 :
(D) 10
Question 11 :
Determine how many two-digit numbers satisfy the following property: when the number is added to the number obtained by reversing its digits, the sum is 132 .
(A) 5
(B) 7
(C) 9
(D) 11
(E) 12
Answer 11 :
(B) 7
Question 12 :
Jefferson Middle School has the same number of boys and girls. $\frac{3}{4}$ of the girls and $\frac{2}{3}$ of the boys went on a field trip. What fraction of the students on the field trip were girls?
(A) $\frac{1}{2}$
(B) $\frac{9}{17}$
(C) $\frac{7}{13}$
(D) $\frac{2}{3}$
(E) $\frac{14}{15}$
Answer 12 :
(B) $\frac{9}{17}$
Question 13 :
Two different numbers are randomly selected from the set ${-2,-1,0,3,4,5}$ and multiplied together. What is the probability that the product is 0 ?
(A) $\frac{1}{6}$
(B) $\frac{1}{5}$
(C) $\frac{1}{4}$
(D) $\frac{1}{3}$
(E) $\frac{1}{2}$
Answer 13 :
(D) $\frac{1}{3}$
Question 14 :
Karl's car uses a gallon of gas every 35 miles, and his gas tank holds 14 gallons when it is full. One day, Karl started with a full tank of gas, drove 350 miles, bought 8 gallons of gas, and continued driving to his destination. When he arrived, his gas tank was half full. How many miles did Karl drive that day?
(A) 525
(B) 560
(C) 595
(D) 665
(E) 735
Answer 14 :
(A) 525
Question 15 :
What is the largest power of 2 that is a divisor of $13^4-11^4 ?$
(A) 8
(B) 16
(C) 32
(D) 64
(E) 128
Answer 15 :
(C) 32
Question 16 :
Annie and Bonnie are running laps around a 400 -meter oval track. They started together, but Annie has pulled ahead, because she runs $25 \%$ faster than Bonnie. How many laps will Annie have run when she first passes Bonnie?
(A) $1 \frac{1}{4}$
(B) $3 \frac{1}{3}$
(C) 4
(D) 5
(E) 25
Answer 16 :
(D) 5
Question 17 :
An ATM password at Fred's Bank is composed of four digits from 0 to 9 , with repeated digits allowable. If no password may begin with the sequence $9,1,1$, then how many passwords are possible?
(A) 30
(B) 7290
(C) 9000
(D) 9990
(E) 9999
Answer 17 :
(D) 9990
Question 18 :
In an All-Area track meet, 216 sprinters enter a 100 - meter dash competition. The track has 6 lanes, so only 6 sprinters can compete at a time. At the end of each race, the five non-winners are eliminated, and the winner will compete again in a later race. How many races are needed to determine the champion sprinter?
(A) 36
(B) 42
(C) 43
(D) 60
(E) 72
Answer 18 :
(C) 43
Question 19 :
The sum of 25 consecutive even integers is 10,000 . What is the largest of these 25 consecutive integers?
(A) 360
(B) 388
(C) 412
(D) 416
(E) 424
Answer 19 :
(E) 424
Question 20 :
The least common multiple of $a$ and $b$ is 12 , and the least common multiple of $b$ and $c$ is 15 . What is the least possible value of the least common multiple of $a$ and $c$ ?
(A) 20
(B) 30
(C) 60
(D) 120
(E) 180
Answer 20 :
(A) 20
Question 21 :
A top hat contains 3 red chips and 2 green chips. Chips are drawn randomly, one at a time without replacement, until all 3 of the reds are drawn or until both green chips are drawn. What is the probability that the 3 reds are drawn?
(A) $\frac{3}{10}$
(B) $\frac{2}{5}$
(C) $\frac{1}{2}$
(D) $\frac{3}{5}$
(E) $\frac{7}{10}$
Answer 21 :
(B) $\frac{2}{5}$
Question 22 :
Rectangle $D E F A$ below is a $3 \times 4$ rectangle with $D C=C B=B A=1$. The area of the "bat wings" (shaded area) is
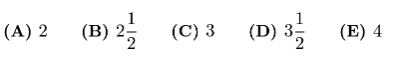
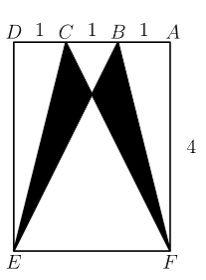
Answer 22 :
(C) 3
Question 23 :
Two congruent circles centered at points $A$ and $B$ each pass through the other circle's center. The line containing both $A$ and $B$ is extended to intersect the circles at points $C$ and $D$. The circles intersect at two points, one of which is $E$. What is the degree measure of $\angle C E D$ ?
(A) 90
(B) 105
(C) 120
(D) 135
(E) 150
Answer 23 :
(C) 120
Question 24 :
The digits $1,2,3,4$, and 5 are each used once to write a five-digit number $P Q R S T$. The three-digit number $P Q R$ is divisible by 4 , the threedigit number $Q R S$ is divisible by 5 , and the three-digit number $R S T$ is divisible by 3 . What is $P$ ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Answer 24 :
(A) 1
Question 25 :
A semicircle is inscribed in an isosceles triangle with base 16 and height 15 so that the diameter of the semicircle is contained in the base of the triangle as shown. What is the radius of the semicircle?
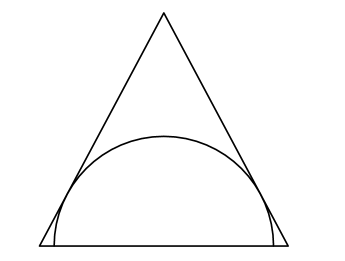
Answer 25 :