Andy and Betsy both live in Mathville. Andy leaves Mathville on his bicycle at $1: 30$ traveling due north at a steady 8 miles per hour. Betsy leaves on her bicycle from the same point at 2:30, traveling due east at a steady 12 miles per hour. At what time will they be exactly the same distance from their common starting point?
(A) $3: 30$
(B) $3: 45$
(C) $4: 00$
(D) $4: 15$
(E) $4: 30$
We can see that at $2: 30$, Andy will be 8 miles ahead. For every hour that they both travel, Betsy will gain 4 miles on Andy. Therefore, it will take 2 more hours for Betsy to catch up, and they will be at the same point at 4:30.
A box contains 10 pounds of a nut mix that is 50 percent peanuts, 20 percent cashews, and 30 percent almonds. A second nut mix containing 20 percent peanuts, 40 percent cashews, and 40 percent almonds is added to the box resulting in a new nut mix that is 40 percent peanuts. How many pounds of cashews are now in the box?
(A) 3.5
(B) 4
(C) 4.5
(D) 5
(E) 6
$$We are given $0.2(10)=2$ pounds of cashews in the first box.
Denote the pounds of nuts in the second nut mix as $x$.
$$
\begin{gathered}
5+0.2 x=0.4(10+x) \
0.2 x=1 \
x=5
\end{gathered}
$$
Thus, we have 5 pounds of the second mix.
$$
0.4(5)+2=2+2=4
$$
How many isosceles triangles are there with positive area whose side lengths are all positive integers and whose longest side has length $2025 ?$
(A) 2025
(B) 2026
(C) 3012
(D) 3037
(E) 4050
You can split the problem into two cases:
Case 1: The two sides with equal length are both smaller than 2025, which means that they range from 1013 to 2024. There are 1012 such cases.
Case 2 : There are two sides of length 2025 , so the last side must be in the range 1 to 2025 . There are 2025 such cases. Keep in mind, an equilateral triangle also counts as an isosceles triangle, since it has at least 2 sides of equal length.
Therefore, the total number of cases is 1012+2025= 3037
A team of students is going to compete against a team of teachers in a trivia contest. The total number of students and teachers is 15 . Ash, a cousin of one of the students, wants to join the contest. If Ash plays with the students, the average age on that team will increase from 12 to 14 . If Ash plays with the teachers, the average age on that team will decrease from 55 to 52 . How old is Ash?
(A) 28
(B) 29
(C) 30
(D) 32
(E) 33
When Ash joins a team, the team's average is pulled towards his age. Let $A$ be Ash's age and $N$ be the number of people on the student team. This means that there are $15-N$ people in the teacher team. Let us write an expression for the change in the average for each team.
The students originally had an average of 12 , which became 14 when Ash joined, so there was an increase of 2 . The term $A-12$ represents how much older Ash is compared to the average of the students'. If we divide this by $N+1$, which is the number of people on the student team when Ash joins, we get the average change per team member once Ash is added. Therefore,
$$
\frac{A-12}{N+1}=2 .
$$
Similarly, for teachers, the average was originally 55 , which decreased by 3 to become 52 when Ash joined. Intuitively, $55-A$ represents how much younger Ash is than the average age of the teachers. Dividing this by the expression $(15-N)+1$, which is the new total number of people on the teacher team, represents the average change per team member once Ash joins. We can write the equation
$$
\frac{55-A}{16-N}=3
$$
To solve the system, multiply equation (1) by $N+1$, and similarly multiply equation (2) by $16-N$. Then add the equations together, canceling $A$, leaving equation $43=50-N$. From this we get $N=7$ and A =28.
Consider the sequence of positive integers
$$
1,2,1,2,3,2,1,2,3,4,3,2,1,2,3,4,5,4,3,2,1,2,3,4,5,6,5,4,3,2,1,2, \ldots
$$
What is the 2025th term in this sequence?
(A) 5
(B) 15
(C) 16
(D) 44
(E) 45
One possible way the sequence could've been constructed was by putting "mountains" going up from 1 , to $n+1$, then going back down to 2 . For example, the first few "mountains" look like this:
$$
12|1232| 123432|12345432| \ldots
$$
So, the $n^{\text {th }}$ mountain has length $2 n$ and has highest number $n+1$. We want to add mountains until we get a total length as close as possible, but not exceeding, 2025. Let the last mountain we sum be mountain $a$. Hence,
$$
\begin{gathered}
2+4+6+\ldots+2 a=2(1+2+3+\ldots+a)=a(a+1) \leq 2025 \
\Longrightarrow a^2<2025 \Longrightarrow a<45
\end{gathered}
$$
so our max $a$ is 44 . In this $44^{\text {th }}$ mountain, the max number is 45 , so the $45^{\text {th }}$ mountain has max number 46 . Next, $44(44+1)=1980$, so we're looking for the $45^{\text {th }}$ number in the $45^{\text {th }}$ mountain, which is 45 .
In an equilateral triangle each interior angle is trisected by a pair of rays. The intersection of the interiors of the middle $20^{\circ}$-angle at each vertex is the interior of a convex hexagon. What is the degree measure of the smallest angle of this hexagon?
(A) 80
(B) 90
(C) 100
(D) 110
(E) 120
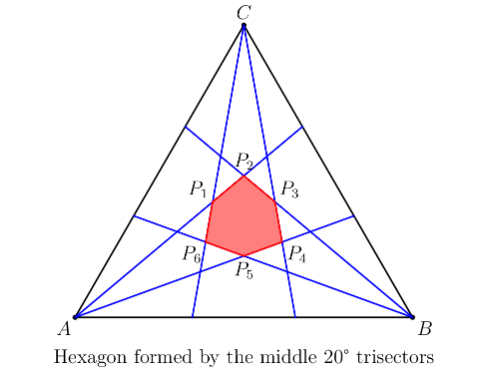
Assume you have a diagram in front of you.
Because each angle of the triangle is trisected, we have $920^{\circ}$ angles. Using a side of the triangle as a base, we have an isosceles triangle with two $20^{\circ}$ angles. Using this we can show that the third angle is $140^{\circ}$.
Following that, we use the principle of vertical angles to show that one angle of the hexagon is $140^{\circ}$. And with rotational symmetry, three. The average of all 6 angles has to be $120^{\circ}$, so the answer is 100
Suppose $a$ and $b$ are real numbers. When the polynomial $x^3+x^2+a x+b$ is divided by $x-1$, the remainder is 4 . When the polynomial is divided by $x-2$, the remainder is 6 . What is $b-a$ ?
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18
Use synthetic division to find that the remainder of $x^3+x^2+a x+b$ is $a+b+2$ when divided by $x-1$ and $2 a+b+12$ when divided by $x-2$. Now, we solve
$$
\left{\begin{array}{l}
a+b+2=4 \
2 a+b+12=6
\end{array}\right.
$$
This ends up being $a=-8, b=10$, so $b-a=10-(-8)= 18
Agnes writes the following four statements on a blank piece of paper.
Each statement is either true or false. How many false statements did Agnes write on the paper?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
We first number all the statements:
1) At least one of these statements is true. 2) At least two of these statements are true. 3) At least two of these statements are false. 4) At least one of these statements is false.
We can immediately see that statement 4 must be true, as it would contradict itself if it were false. Similarly, statement 1 must be true, as all the other statements must be false if it were false, which is contradictory because statement 4 is true. Since both 1 and 4 are true, statement 2 has to be true. Therefore, statement 3 is the only false statement, making the answer 1.
Let $f(x)=100 x^3-300 x^2+200 x$. For how many real numbers $a$ does the graph of $y=f(x-a)$ pass through the point $(1,25)$ ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) more than 4
Substitute $1-a$ for $x$ and set this expression equal to 25 . The problem boils down to finding how many real roots
$$
100(1-a)^3-300(1-a)^2+200(1-a)=25
$$
has. We further simplify this expression and create a function $f(x)$ :
$$
f(x)=-100 a^3+100 a-25
$$
Using Descarte's Rule of Signs we get:
Sign changes for $f(x)$ (possible number of positive roots): 2
$$
f(-x)=+100 a^3-100 a-25
$$
Sign changes for $f(-x)$ (possible number of negative roots): 1
Possibilities for roots:
1) 2 positive roots, 1 negative root
2) 0 positive roots, 1 negative root, 2 imaginary roots
So which one is it? We know if the function changes sign between an interval, then a root exists in that interval. From $a=0$ to $\frac{1}{2}$, the function changes sign because $f(0)=-25$ while $f\left(\frac{1}{2}\right)=+\frac{25}{2}$, so a positive root exists. This eliminates the second possibility, implying that there must be 2 positive and 1 negative roots. So the answer is $2+1= 3$.
A semicircle has diameter $\overline{A B}$ and chord $\overline{C D}$ of length 16 parallel to $\overline{A B}$. A smaller semicircle with diameter on $\overline{A B}$ and tangent to $\overline{C D}$ is cut from the larger semicircle, as shown below.
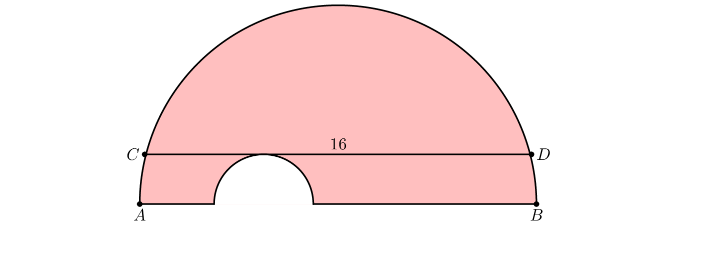
What is the area of the resulting figure, shown shaded?
(A) $16 \pi$
(B) $24 \pi$
(C) $32 \pi$
(D) $48 \pi$
(E) $64 \pi$
The problem doesn't restrict where the smaller semicircle is along the larger semicircle's diameter. Therefore, we can assume that the two semicircles are concentric. Let the center of both semicircles be $O$, and let $C D$ be tangent to the smaller semicircle at $T$. Let the radius of the smaller semicircle be $x$, and let the radius of the larger semicircle be $r$. If we mirror the diagram over $A B$, we can see that we have two concentric circles. We are trying to find $\pi\left(\frac{r^2-x^2}{2}\right)$. By Power of a Point on $T$, we can see that
$$
64=(r+x)(r-x)=r^2-x^2
$$
Thus, $\pi\left(\frac{r^2-x^2}{2}\right)=32$
The sequence $1, x, y, z$ is arithmetic. The sequence $1, p, q, z$ is geometric. Both sequences are strictly increasing and contain only integers, and $z$ is as small as possible. What is the value of $x+y+z+p+q$ ?
(A) 66
(B) 91
(C) 103
(D) 132
(E) 149
Since $1, x, y, z$ is an arithmetic sequence, we have $y=2 x-1$ and $z=3 x-2$. Since $1, p, q, z$ is a geometric sequence, we have $q=p^2$ and $z=p^3$. Thus $p^3=3 x-2$.
Because $p^3 \equiv p(\bmod 3)$, we get $3 x-2 \equiv p(\bmod 3)$, so $p \equiv 1(\bmod 3)$. The smallest integer $p>1$ satisfying this is $p=4$.
Then $64=3 x-2 \rightarrow x=22, y=43, z=64, q=16$. Therefore, $x+y+z+p+q=22+43+64+4+16= 149$.
Carlos uses a 4-digit passcode to unlock his computer. In his passcode, exactly one digit is even, exactly one (possibly different) digit is prime, and no digit is 0 . How many 4 -digit passcodes satisfy these conditions?
(A) 176
(B) 192
(C) 432
(D) 464
(E) 608
The only two digits that are neither prime nor even are 1 and 9 . We split this problem into cases based on the number of 2 s . This is because 2 is both a prime number and an even number.
Case 1: For this case, there are no 2s. For this case, there are 4 choices for where the even digit goes, and 3 choices for what the even digit is. There are then 3 choices for where the prime digit goes, and 3 choices for what the prime digit is. The last two spots have 2 choices each, 1 or 9 . This gives a total of $4 \cdot 3^3 \cdot 2^2=432$ options for this case.
Case 2: For this case, there is one 2 . There are 4 choices for where 2 goes, and 2 choices for the other three digits each. This case gives a total of $2^3 \cdot 4=32$ options!
Hence, the answer is $432+32=464$
In the figure below, the outside square contains infinitely many squares, each of them with the same center and sides parallel to the outside square. The ratio of the side length of a square to the side length of the next inner square is $k$, where $0<k<1$. The spaces between squares are alternately shaded as shown in the figure (which is not necessarily drawn to scale).

The area of the shaded portion of the figure is $64 \%$ of the area of the original square. What is $k$ ?
(A) $\frac{3}{5}$
(B) $\frac{16}{25}$
(C) $\frac{2}{3}$
(D) $\frac{3}{4}$
(E) $\frac{4}{5}$
Let the side length of the largest square be $a$, so it has area $a^2$. Hence, the second-largest square has area $a^2 k^2$, the third-largest has $a^2 k^4$, and so on.
It follows that the total shaded area is
$$
a^2-a^2 k^2+a^2 k^4-a^2 k^6+\ldots=a^2\left(1-k^2+k^4-k^6+\ldots\right)=a^2 \frac{1}{1+k^2}
$$
The ratio of the area of the shaded region to that of the original square is then
$$
\begin{gathered}
\frac{a^2 \frac{1}{1+k^2}}{a^2}=\frac{1}{1+k^2}=\frac{64}{100} \
\Longrightarrow 64+64 k^2=100 \Longrightarrow k^2=\frac{36}{64} \Longrightarrow k= \frac{3}{4} .
\end{gathered}
$$
Six chairs are arranged around a round table. Two students and two teachers randomly select four of the chairs to sit in. What is the probability that the two students will sit in two adjacent chairs and the two teachers will also sit in two adjacent chairs?
(A) $\frac{1}{6}$
(B) $\frac{1}{5}$
(C) $\frac{2}{9}$
(D) $\frac{3}{13}$
(E) $\frac{1}{4}$
Pair two students together and put them adjacent on any two seats. There are 6 ways to do this. Considering one of these cases (they are all the same), there are 4 seats left, in which we wish to arrange the teachers together. So pair the teachers together and put them adjecent on any two seats not already occupied by two of the students. There are 3 ways to do this. For all 6 cases, there are $6 \times 3=18$ favorable outcomes.
The number of ways to arrange the 2 students and 2 teachers is $\binom{6}{2} \times\binom{ 4}{2}=90$.
Our probability is $\frac{18}{90}={5}$
In the figure below, $A B E F$ is a rectangle, $\overline{A D} \perp \overline{D E}, A F=7, A B=1$, and $A D=5$.
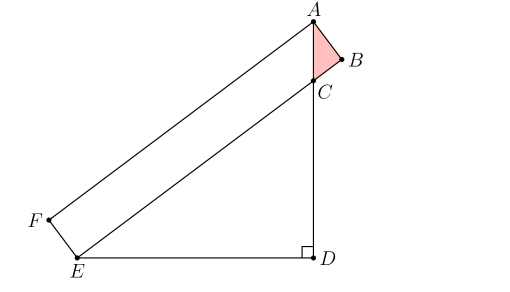
What is the area of $\triangle A B C ?$
(A) $\frac{3}{8}$
(B) $\frac{4}{9}$
(C) $\frac{1}{8} \sqrt{13}$
(D) $\frac{7}{15}$
(E) $\frac{1}{8} \sqrt{15}$
Because $A B E F$ is a rectangle, $\angle A B C=90$. We are given that $\angle A D E=90$, and since $\angle E C D=\angle A C B$ by vertical angles, $\triangle E C D \sim \triangle A C B$. Let $A C=x$. By the Pythagorean Theorem, $C B=\sqrt{x^2-1}$. Since $A F=B E=7, E C=7-\sqrt{x^2-1}$. Because $A C=x$ and $A D=5, C D=5-x$. By similar triangles,
$$
\frac{7-\sqrt{x^2-1}}{x}=\frac{5-x}{\sqrt{x^2-1}}
$$
. Cross-multiplying, we get that
$$
7 \sqrt{x^2-1}-x^2+1=5 x-x^2
$$
, so
$$
7 \sqrt{x^2-1}=5 x-1
$$
. We square both sides, and this is simply a quadratic in $x$ :
$$
24 x^2+10 x-50=0
$$
, which has a positive root $x=\frac{5}{4}$. Since $A B=1$, we can plug this into the Pythagorean Theorem, with $\frac{5}{4}$ being the hypotenuse, to get $B C=\frac{3}{4}$, and $1 \cdot \frac{\frac{3}{4}}{2}$ to equal $[A B C]= \frac{3}{8}$
There are three jars. Each of three coins is placed in one of the three jars, chosen at random and independently of the placements of the other coins. What is the expected number of coins in a jar with the most coins?
(A) $\frac{4}{3}$
(B) $\frac{13}{9}$
(C) $\frac{5}{3}$
(D) $\frac{17}{9}$
(E) 2
We have three coins and three jars. Each coin is placed independently and randomly into one of the jars. Let $M$ be the maximum number of coins in any jar. We want to compute the expected value of $M$.
Step 1: Count total outcomes
Each coin has 3 choices, so the total number of equally likely placements is $3^3=27$.
Step 2: Casework on the maximum number of coins
Case 1: $M=1$. This occurs when each jar has exactly one coin. There are $3!=6$ assignments of coins to jars. Hence, $\operatorname{Pr}(M=1)=\frac{6}{27}=\frac{2}{9}$.
Case 2: $M=3$. This occurs when all three coins fall into the same jar. There are 3 jars to choose from, so $\operatorname{Pr}(M=3)=\frac{3}{27}=\frac{1}{9}$.
Case 3: $M=2$. This occurs when one jar has 2 coins, another jar has 1 coin, and the last jar has 0 coins. We can choose which jar gets 2 coins in 3 ways, which jar gets 1 coin in 2 ways, and which 2 coins out of the 3 go into the jar with two coins, so we multiply by $\binom{3}{2}$, which is just 3 (note we don't have to do this for the earlier cases because for case 2 , all 3 coins go into one jar, and for case 1 , the factorial already accounts for that). Therefore, there are $3^2 \cdot 2=18$ outcomes. Thus, $\operatorname{Pr}(M=2)=\frac{18}{27}=\frac{2}{3}$.
Step 3: Compute the expected value The expected value of $M$ is $\mathbb{E}[M]=1 \cdot \frac{2}{9}+2 \cdot \frac{2}{3}+3 \cdot \frac{1}{9}$. Converting everything to ninths, we have $\mathbb{E}[M]=\frac{2}{9}+\frac{12}{9}+\frac{3}{9}=\frac{17}{9}$.
Hence, the expected number of coins in the jar with the most coins is $\frac{17}{9}$.
Let $N$ be the unique positive integer such that dividing 273436 by $N$ leaves a remainder of 16 and dividing 272760 by $N$ leaves a remainder of 15 . What is the tens digit of $N$ ?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
The problem statement implies that $N$ divides both $273436-16=273420$ and $272760-15=272745$. We want to find $N>16$ that satisfies both of these conditions. Hence, we can just find the greatest common divisor of the two numbers. $\operatorname{gcd}(273420,272745)=\operatorname{gcd}(675,272745)=\operatorname{gcd}(675,45)=45$ by the Euclidean Algorithm, so the answer is 4.
The harmonic mean of a collection of numbers is the reciprocal of the arithmetic mean of the reciprocals of the numbers in the collection. For example, the harmonic mean of 4,4 , and 5 is
$$
\frac{1}{\frac{1}{3}\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{5}\right)}=\frac{30}{7}
$$
What is the harmonic mean of all the real roots of the 4050th degree polynomial
$$
\prod_{k=1}^{2025}\left(k x^2-4 x-3\right)=\left(x^2-4 x-3\right)\left(2 x^2-4 x-3\right)\left(3 x^2-4 x-3\right) \ldots\left(2025 x^2-4 x-3\right) ?
$$
(A) $-\frac{5}{3}$
(B) $-\frac{3}{2}$
(C) $-\frac{6}{5}$
(D) $-\frac{5}{6}$
(E) $-\frac{2}{3}$
We will need to determine the sum of the reciprocals of the roots. To find the sum of the reciprocals of the roots $p, q$ of the quadratic $a x^2+b x+c$, we use Vieta's formulas. Recall that $p+q=-b / a$ and $p q=c / a$. Therefore,
$$
\frac{1}{p}+\frac{1}{q}=\frac{p+q}{p q}=\frac{\frac{-b}{a}}{\frac{c}{a}}=\frac{-b}{a} \cdot \frac{a}{c}=\frac{-b}{c}
$$
which doesn't depend on $a$.
The sum of the reciprocals of the roots of the quadratic $x^2-4 x-3$ is $\frac{-(-4)}{-3}=-4 / 3$. The same is true for every quadratic in the form $a x^2-4 x-3$. The sum of all the reciprocals of the roots of $a x^2+b x+c$ is $2025 \cdot\left(-\frac{4}{3}\right)$.
Because we have 2025 quadratics, there are $2 \cdot 2025=4050$ total roots. Our answer is $\frac{1}{\frac{1}{4050} \cdot \frac{-4 \cdot 2025}{3}}=-\frac{3}{2}$.
An array of numbers is constructed beginning with the numbers $-1 \quad 3 \quad 1$ in the top row. Each adjacent pair of numbers is summed to produce a number in the next row. Each row begins and ends with -1 and 1 , respectively.
$$
\begin{array}{cccccccc}
& & -1 & & 3 & & 1 & \
& & & & & & & \
-1 & & 2 & & 4 & & 1 & \
& & & & & & & \
-1 & 1 & & 6 & & 5 & & 1
\end{array}
$$
If the process continues, one of the rows will sum to 12,288 . In that row, what is the third number from the left?
(A) -29
(B) -21
(C) -14
(D) -8
(E) -3
Consider the polynomial $f(x)=-x^2+3 x+1$. When we multiply this polynomial by $x+1$, we are essentially doing the operation given in the problem (When we multiply $p(x)$ by $x+1$, a term of degree $d$ in the yielded expression is the sum of $1 \cdot$ (degree d ) and $x \cdot$ (degree $\mathrm{d}-1$ ) in $p(x)$ This effect is visible in Pascal's Triangle). So, if we let the coefficients of $f(x)$ be the zero row of the array, then the $n^{\text {th }}$ row is just the coefficients of $f(x)(x+1)^n$. The next thing to note is that the sum of the coefficients in any polynomial $p(x)$ is just $p(1)$. Therefore, the sum of the entries in the $n^{\text {th }}$ row of the array is $f(1)(1+1)^n=3 \cdot 2^n$. Letting this equal 12288 , we get $n=12$. We are looking for the $3^{\text {rd }}$ term in the $12^{\text {th }}$ row. The $12^{\text {th }}$ row is given by the coefficients of $f(x)(x+1)^{12}=\left(-x^2+3 x+1\right)(x+1)^{12}$. Since the degree of the resulting expression is 14 , the third term in the row is just the coefficient of $x^{12}$ in the expression, which is $-\binom{12}{10}+3\binom{12}{11}+1=-29$.
A silo (right circular cylinder) with diameter 20 meters stands in a field. MacDonald is located 20 meters west and 15 meters south of the center of the silo. McGregor is located 20 meters east and $g>0$ meters south of the center of the silo. The line of sight between MacDonald and McGregor is tangent to the silo. The value of $g$ can be written as $\frac{a \sqrt{b}-c}{d}$, where $a, b, c$, and $d$ are positive integers, $b$ is not divisible by the square of any prime, and $d$ is relatively prime to the greatest common divisor of $a$ and $c$. What is $a+b+c+d$ ?
(A) 119
(B) 120
(C) 121
(D) 122
(E) 123
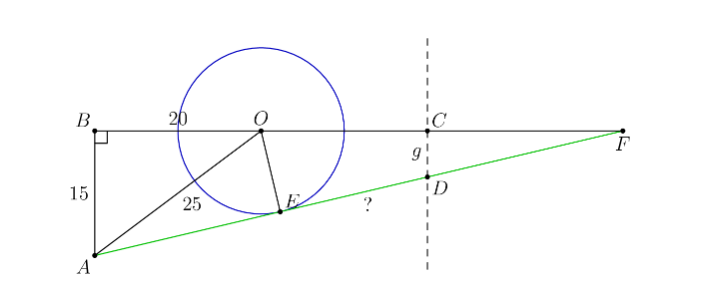
Let the silo center be $O$, let the point MacDonald is situated at be $A$, and let the point 20 meters west of the silo center be $B . A B O$ is then a right triangle with side lengths 15,20 , and 25 .
Let the point 20 meters east of the silo center be $C$, and let the point McGregor is at be $D$ with $C D=g>0$. Also let $A D$ be tangent to circle $O$ at $E$.
Extend $B C$ and $A D$ to meet at point $F$. This creates 3 similar triangles, $\triangle A B F \sim \triangle D C F \sim \triangle O E F$. Let the distance between point $C$ and $F$ be $x$. The similarity ratio between triangles $A B F$ and $D C F$ is then $\frac{\text { longer leg }}{\text { shorter leg }}=\frac{40+x}{15}=\frac{x}{g}$
This is currently unsolvable so we bring in triangle $O E F$. The hypotenuse of triangle $O E F$ is $O F=20+x$ and its shorter leg is the radius of the silo $=10$. We can then establish a second similarity relationship between triangles $O E F$ and $A B F$ with $\frac{\text { shorter leg }}{\text { hypotenuse }}=\frac{10}{20+x}=\frac{15}{A F}$
Now we find the hypotenuse of $A B F$ in terms of $x$ using the Pythagorean theorem. $A F^2=15^2+(40+x)^2$. Which simplifies to $A F^2=225+1600+80 x+x^2=1825+80 x+x^2$ So $A F=\sqrt{x^2+80 x+1825}$
Plugging back in we get $\frac{10}{20+x}=\frac{15}{\sqrt{x^2+80 x+1825}}$. Now we can begin to break this down by multiplying both sides by both denominators. $10\left(\sqrt{x^2+80 x+1825}\right)=15(20+x)$ Dividing both sides by 5 then squaring yields, $4 x^2+320 x+7300=9 x^2+360 x+3600$ This furthermore simplifies to $5 x^2+40 x-3700=0$ At which point we can divide off a 5 and then apply the quadratic formula on $x^2+8 x-740=0$ which we take the positive root of.
$$
x=\frac{-8+\sqrt{64+2960}}{2}=\frac{-8+\sqrt{3024}}{2}=\frac{-8+\sqrt{144 \cdot 21}}{2} .
$$
Simplifying yields that $x=6 \sqrt{21}-4$
Then to solve for $g$ we simply plug $6 \sqrt{21}-4$ back into the first similarity ratio to get $\frac{36+6 \sqrt{21}}{15}=\frac{6 \sqrt{21}-4}{g}$
Multiply both sides by $15 g$ and dividing by $36+6 \sqrt{21}$ will let us solve for $g=\frac{15(6 \sqrt{21}-4)}{36+6 \sqrt{21}}$ and after rationalizing the denominator we get $\frac{20 \sqrt{21}-75}{3} \cdot 20+21+75+3=119$
A set of numbers is called sum-free if whenever $x$ and $y$ are (not necessarily distinct) elements of the set, $x+y$ is not an element of the set. For example, ${1,4,6}$ and the empty set are sum-free, but ${2,4,5}$ is not. What is the greatest possible number of elements in a sum-free subset of ${1,2,3, \ldots, 20}$ ?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
Let our subset be ${11,12,13, \ldots, 20}$. If we add any element from the set ${1,2,3, \ldots, 10}$ to our current subset, we will have to remove at least one element from our subset. Hence, the maximum size of our subset is 10 .
A circle of radius $r$ is surrounded by three circles, whose radii are 1,2 , and 3 , all externally tangent to the inner circle and externally tangent to each other, as shown in the diagram below.
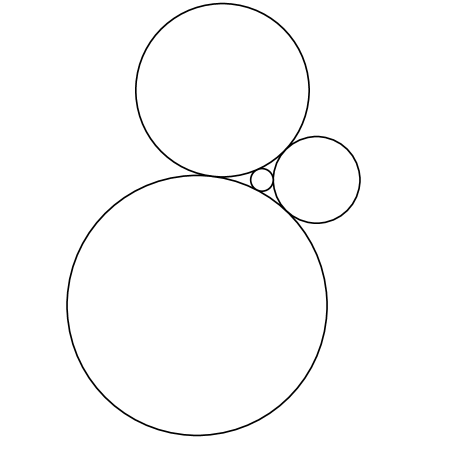
What is $r$ ?
(A) $\frac{1}{4}$
(B) $\frac{6}{23}$
(C) $\frac{3}{11}$
(D) $\frac{5}{17}$
(E) $\frac{3}{10}$
Descartes' Circle Formula (curvatures $k_i=\frac{1}{r_i}$ )
$$
k_4=k_1+k_2+k_3 \pm 2 \sqrt{k_1 k_2+k_2 k_3+k_3 k_1}
$$
For radii $1,2,3$ we have
$$
k_1=1, \quad k_2=\frac{1}{2}, \quad k_3=\frac{1}{3}
$$
Compute the sum and the square-root term
$$
k_1+k_2+k_3=\frac{11}{6}, \quad k_1 k_2+k_2 k_3+k_3 k_1=1
$$
Therefore
$$
k_4=\frac{11}{6} \pm 2
$$
Choose the plus sign for the small circle tangent externally to the three given circles
$$
k_4=\frac{11}{6}+2=\frac{23}{6}, \quad r_4=\frac{1}{k_4}=\frac{6}{23}
$$
Triangle $\triangle A B C$ has side lengths $A B=80, B C=45$, and $A C=75$. The bisector of $\angle B$ and the altitude to side $\overline{A B}$ intersect at point $P$. What is $B P$ ?
(A) 18
(B) 19
(C) 20
(D) 21
(E) 22
Let $C D \perp A B$ with foot $D$. Right triangles $A C D$ and $B C D$ give $A C^2=A D^2+C D^2, B C^2=B D^2+C D^2$,
$$
A C^2-B C^2=A D^2-B D^2=(A D-B D)(A D+B D)
$$
Since $A D+B D=A B=80$ and $A C^2-B C^2=75^2-45^2=3600$, we get the equation $3600=80(A D-B D)$. This equation simplifies to $45=A D-B D$. We can solve the system of equations $A D+B D=80$ and $A D-B D=45$ easily via elimination, and we
$$
\text { get } A D=\frac{125}{2}, B D=\frac{35}{2} . C D^2=A C^2-A D^2=75^2-\left(\frac{125}{2}\right)^2=\frac{6875}{4}, C D=\frac{25 \sqrt{11}}{2} \text {. }
$$
By Angle Bisector Theorem, $\frac{D P}{P C}=\frac{D B}{B C}=\frac{\frac{35}{2}}{45}=\frac{7}{18}, P C=C D-D P$ thus, $18 D P=7(C D-D P), 25 D P=7 C D$,
$$
\begin{aligned}
& D P=\left(\frac{7}{25}\right) C D=\left(\frac{7}{25}\right)\left(\frac{25 \sqrt{11}}{2}\right)=\frac{7 \sqrt{11}}{2} \
& B P^2=B D^2+D P^2=\left(\frac{35}{2}\right)^2+\left(\frac{7 \sqrt{11}}{2}\right)^2=\frac{1225}{4}+\frac{49(11)}{4}=\frac{1764}{4}=441, \text { thus } B P= 21 .
\end{aligned}
$$
Call a positive integer fair if no digit is used more than once, it has no 0s, and no digit is adjacent to two greater digits. For example, 196, 23, and 12463 are fair, but 1546,320 , and 34321 are not fair. How many fair positive integers are there?
(A) 511
(B) 2584
(C) 9841
(D) 17711
(E) 19682
Note every fair number will have an increasing string of digits, a maximum digit, then a decreasing string of digits. This is because if it decreases then increases, then the digit in the middle will be less than its adjacent digits.
Let $n$ be the maximum digit. For each number $i<n$, we may either place $i$ before $n$, after $n$, or choose not to include it. Note this process will result in a unique number for every case, as the numbers before $n$ must be in increasing order, and the numbers after $n$ must be in decreasing order. Therefore, for each number $n$, we have $3^{n-1}$ cases.
Since $n \in{1,2, \cdots 9}$, we have:
$$
\sum_{n=1}^9 3^{n-1}=\frac{3^9-1}{3-1}=9841
$$
A point $P$ is chosen at random inside square $A B C D$. The probability that $\overline{A P}$ is neither the shortest nor the longest side of $\triangle A P B$ can be written as $\frac{a+b \pi-c \sqrt{d}}{e}$, where $a, b, c, d$, and $e$ are positive integers, $\operatorname{gcd}(a, b, c, e)=1$, and $d$ is not divisible by the square of a prime. What is $a+b+c+d+e$ ?
(A) 25
(B) 26
(C) 27
(D) 28
(E) 29
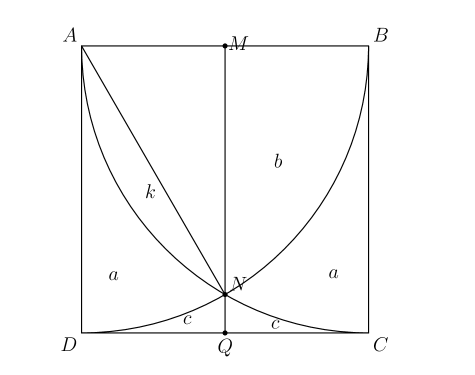
Assume the sides of this square is 1 , hence we only need to find the area of the desired regions. From Solution 1, it is easy to see that the regions are the bottom left region c and the top right region b , hence we must compute $b+c$. Also, define $k$ to be the circular segment. We have two equations right off the bat:
$2 a+2 b+2 c=1 \Longrightarrow a+b+c=\frac{1}{2}$ since the sum of all regions is just the area of the square and also, $2 b+a=\frac{\pi}{4}$, just the area of a quarter-circle.
Next, $\triangle A B N$ has a area of $\frac{\sqrt{3}}{4}$ since it is just an equilateral triangle with length 1 (each side is a radius of a circle with radius of 1 ). From the diagram, $2 k+[A B N]=2 k+\frac{\sqrt{3}}{4}=2 b$. Subsequently, we see that sector $A D N$ has an angle of $90-60=30$ and is the sum of $a+k$. Therefore, $a+k=\frac{\pi}{12}$.
Multiply this equation by 2 : $2 a+2 k=\frac{\pi}{6}$ and combining it with $2 b-2 k=\frac{\sqrt{3}}{4}$ yields $2 a+2 b=\frac{\pi}{6}+\frac{\sqrt{3}}{4}$. Since we also have that $2 b+a=\frac{\pi}{4}$, subtracting this from the equation yields $a=\left(\frac{\pi}{6}+\frac{\sqrt{3}}{4}\right)-\left(\frac{\pi}{4}\right)=\frac{-\pi}{12}+\frac{\sqrt{3}}{4}$. We are to find $b+c=\frac{1}{2}-a=\frac{1}{2}-\left(\frac{\sqrt{3}}{4}-\frac{\pi}{12}\right)=\frac{1}{2}-\frac{\sqrt{3}}{4}+\frac{\pi}{12}=\frac{6+\pi-3 \sqrt{3}}{12}$.
At last, $a+b+c+d+e=6+1+3+3+12= 25$.