AMC 10A,2022,Problem25
Let $R,S$ and $T$,be squares that have vertices at lattice points (i.e.,points whose coordinates are both integers) in the coordinate plane,together with their interiors. The bottom edge of each square is on the $x$-axis.The left edge of $R$ and the right edge of $S$ are on the $y$-axis and $R$ contains $\frac{9}{4}$ as many lattice points as does $S$ .The top two vertices of $T$ are in $R \cup S$,and $T$ contains $\frac{1}{4}$ of the lattice points contained in $R \cup S$.See the figure (not drawn to scale).

The fraction of lattice points in $S$ that are in $S \cap T$ is $27$ imes the fraction of lattice points in $R$ that are in $R \cap T$ . What is the minimum possible value of the edge length of $R$ plus the edge length of $S$ plus the edge length of $T$ ?
A) $336$
B) $337$
C) $338$
D) $339$
E) $340$
AMC 10A,2022,Problem23
Isosceles trapezoid $ABCD$ has parallel sides $\overline{AD}$,and $\overline{BC}$,with $BC<AD$ and $AB=CD $.There is a point $P$ in the plane such that $PA=1,PB=2,PC=3$ and $PD=4$ .What is $\frac{BC}{AD}$
A)$\frac{1}{4}$
B)$\frac{1}{3}$
C)$\frac{1}{2}$
D)$\frac{2}{3}$
E)$\frac{3}{4}$
AMC 10A,2022,Problem21
A bowl is formed by attaching four regular hexagons of side $1$ to a square of side $1$.The edges of the adjacent hexagons coincide,as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons,situated on the rim of the bowl?

A)$6$
B)$7$
C)$5+2\sqrt2$
D)$8$
E)$E$
AMC 10A,2022,Problem15
Quadrilateral $ABCD$ with side lengths $AB=7,BC=24,CD=20,DA=15$ s inscribed in a circle. The area interior to the circle but exterior to the quadrilateral can be written in the form $\frac{a\pi -b}{c}$ where $a,b,c $ are positive integers such that $a$ and $c$ have no common prime factor .What is $a+b+c$ ?
A)$260$
B)$855$
C)$1235$
D)$1565$
E)$1997$

AMC 10A,2022,Problem13
Let $\triangle ABC $ be a scalene triangle point $P$ lies on $\overline{BC}$ so that $\overline{AP}$ bisects $\angle{BAC}$ .The line through $B$ perpendicular to $\overline{AP}$ intersects the line through $A$ parallel to $\overline{BC}$ at the point $D$. Suppose $BP=2 $ and $PC=3$ .What is $AD$ ?
A) $8$
B)$9$
C)$10$
D)$11$
E)$12$

AMC 10A,2022,Problem10
Daniel finds a rectangular index card and measures its diagonal to be $8$ centimeters .Daniel then cuts out equal squares of side $1$ cm t two opposite corners of the index card and measures the distance between the two closest vertices of these squares to be centimeters,as shown below. What is the area of the original index card?
A) $14$
B) $10\sqrt2$
C)16
D)$18\sqrt2$
E)18
AMC 10A,2022,Problem5
Square $ABCD$ has a length $1$.Points $P$,$Q$,$R$ and $S$ each lie on a side of $ABCD$ such that $APQCRS$ is an equilateral convex hexagon with side length s,what is s?
A) $\frac{\sqrt2}{3}$
B) $ \frac{1}{2}$
C) $2-\sqrt2$
D) $1-\frac{\sqrt2}{4}$
E) $\frac{2}{3}$

AMC 10A,2021,Problem 12
Two right circular cones with vertices facing down as shown in the figure below contains the same amount of liquid. The radii of the tops of the liquid surfaces are $3$ cm and $6$ cm.
Into each cone is dropped a spherical marble of radius $1$ cm,which sinks to the bottom and is completely submerged without spilling any liquid.
What is the ratio of the rise of the liquid level in the narrow cone to the rise of the liquid level in the wide cone?

(A) $1:1$
(B) $47:43$
(C) $2:1$
(D) $40:13$
(E) $4:1$
AMC 10A,2021,Problem 13
What is the volume of tetrahedron $ABCD$ with edge lengths $AB=2$,$AC=3$,$AD=4$,$BC=\sqrt{13}$,$BD=2\sqrt{5}$,and $CD=5$ ?
(A) $3$
(B) $2\sqrt{3}$
(C) $4$
(D) $3\sqrt{3}$
(E) $6$
AMC 10A,2021,Problem 17
Trapezoid $ABCD$ has $\overline{AB}\parallel \overline{CD},BC=CD=43$,and $\overline{AD}\perp\overline{BD}$.
Let $O$ be the intersection of the diagonals $\overline{AC}$ and $\overline{BD}$,and let $P$ be the midpoint of $\overline{BD}$.
Given that $OP=11$,the length of $AD$ can be written in the form $m\sqrt{n}$,where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. What is $m+n$?

(A) $65$
(B) $132$
(C) $157$
(D) $194$
(E) $215$
AMC 10A,2021,Problem 19
The area of the region bounded by the graph of $x^2+y^2=3|x-y|+3|x+y|$ is $m+n\pi$,where $m$ and $n$ are integers. What is $m+n$?
(A) $18$
(B) $27$
(C) $36$
(D) $45$
(E) $54$
AMC 10A,2021,Problem 21
Let $ABCDEF$ be an equiangular hexagon. The lines $AB,CD,$ and $EF$ determine a triangle with area $192\sqrt{3}$,and the lines $BC,DE,$ and $FA$ determine a triangle with area $324\sqrt{3}$.
The perimeter of hexagon $ABCDEF$ can be expressed as $m+n\sqrt{p}$,where $m,n,$ and $p$ are positive integers and $p$ is not divisible by the square of any prime. What is $m+n+p$?
(A) $47$ (B) $52$ (C) $55$ (D) $58$ (E) $63$
AMC 10B Problems,2021,Problem 7
In a plane,four circles with radii $1,3,5,$ and $7$ are tangent to line $l$ at the same point $A,$ but they may be on either side of $l$. Region $S$ consists of all the points that lie inside exactly one of the four circles. What is the maximum possible area of region $S$?
(A) $24\pi$
(B) $32\pi$
(C) $64\pi$
(D) $65\pi$
(E) $84\pi$
AMC 10B Problems,2021,Problem 9
The point $P(a,b)$ in the $xy$-plane is first rotated counterclockwise by $90^{\circ}$ around the point $(1,5)$ and then reflected about the line $y=-x$.
The image of $P$ after these two transformations is at $(-6,3)$. What is $b - a ?$
(A) $1$ (B) $3$ (C) $5$ (D) $7$ (E) $9$
AMC 10B Problems,2021,Problem 10
An inverted cone with base radius $12$ cm and height $18$ cm is full of water. The water is poured into a tall cylinder whose horizontal base has a radius of $24$ cm.
What is the height in centimeters of the water in the cylinder?
(A) $1.5$ (B) $3$ (C) $4$ (D) $4.5$ (E) $6$
AMC 10B Problems,2021,Problem 20
The figure is constructed from $11$ line segments,each of which has length $2$. The area of pentagon $ABCDE$ can be written is $\sqrt{m}+\sqrt{n}$,where $m$ and $n$ are positive integers.
What is $m+n ?$

(A) $20$ (B) $21$ (C) $22$ (D) $23$ (E) $24$
AMC 10B Problems,2021,Problem 21
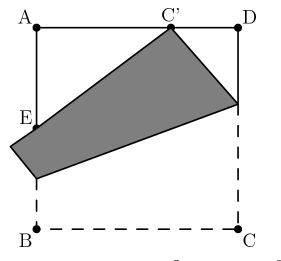
A square piece of paper has side length $1$ and vertices $A,B,C,$ and $D$ in that order. As shown in the figure,the paper is folded so that vertex $C$ meets edge $\overline{AD}$ at point $C'$, and edge $\overline{AB}$ at point $E$. Suppose that $C'D=\frac{1}{3}$.
What is the perimeter of triangle $\bigtriangleup AEC' ?$
(A) $2$
(B) $1+\frac{2}{3} \sqrt{3}$
(C) $\sqrt{136}$
(D) $1 + \frac{3}{4} \sqrt{3}$
(E) $\frac{7}{3}$
AMC 10B Problems, 2021, Problem 23
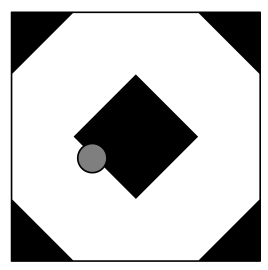
A square with side length $8$ is colored white except for $4$ black isosceles right triangular regions with legs of length $2$ in each corner of the square and a black diamond with side length $2\sqrt{2}$ in the center of the square, as shown in the diagram. A circular coin with diameter $1$ is dropped onto the square and lands in a random location where the coin is completely contained within the square,
The probability that the coin will cover part of the black region of the square can be written as $\frac{1}{196}(a+b\sqrt{2}+\pi)$, where $a$ and $b$ are positive integers. What is $a+b$?
(A) $64$ (B) $66$ (C) $68$ (D) $70$ (E) $72$
AMC 10 A, 2020 , Problem 12
Triangle $AMC$ is isosceles with $AM = AC$. Medians $\overline{MV}$ and $\overline{CU}$ are perpendicular to each other, and $MV=CU=12$.
What is the area of $\triangle AMC?$

(A) $48$ (B) $72$ (C) $ 96$ (D) $144$ (E) $192 $
AMC 10A, 2020, Problem 16
A point is chosen at random within the square in the coordinate plane whose vertices are $(0, 0), (2020, 0), (2020, 2020),$ and $(0, 2020)$.
The probability that the point is within $d$ units of a lattice point is $\frac{1}{2}$.
(A point $(x, y)$ is a lattice point if $x$ and $y$ are both integers.)
What is $d$ to the nearest tenth$?$
(A) $ 0.3$ (B) $0.4$ (C) $0.5$ (D) $0.6$ (E) $0.7$
AMC 10A, 2020, Problem 19
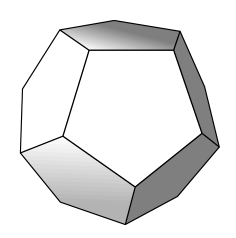
As shown in the figure below, a regular dodecahedron (the polyhedron consisting of $12$ congruent regular pentagonal faces) floats in space with two horizontal faces. Note that there is a ring of five slanted faces adjacent to the top face, and a ring of five slanted faces adjacent to the bottom face. How many ways are there to move from the top face to the bottom face via a sequence of adjacent faces so that each face is visited at most once and moves are not permitted from the bottom ring to the top ring?
(A) $1$ (B) $2$ (C) $3$ (D) $4$ (E) $5$
AMC 10A, 2020, Problem 20
Quadrilateral $ABCD$ satisfies $\angle ABC = \angle ACD = 90^{\circ}, AC=20,$ and $CD=30.$ Diagonals $\overline{AC}$ and $\overline{BD}$ intersect at point $E,$ and $AE=5.$ What is the area of quadrilateral $ABCD?$
(A) $330$ (B) $340$ (C) $350$ (D) $360$ (E) $370$
AMC 10A, 2020, Problem 23
Let $T$ be the triangle in the coordinate plane with vertices $(0,0), (4,0),$ and $(0,3).$ Consider the following five isometries (rigid transformations) of the plane: rotations of $90^{\circ}, 180^{\circ},$ and $270^{\circ}$ counterclockwise around the origin, reflection across the $x$-axis, and reflection across the $y$-axis. How many of the $125$ sequences of three of these transformations (not necessarily distinct) will return $T$ to its original position?
(For example, a $180^{\circ}$ rotation, followed by a reflection across the $x$-axis, followed by a reflection across the $y$-axis will return $T$ to its original position, but a $90^{\circ}$ rotation, followed by a reflection across the $x$-axis, followed by another reflection across the $x$-axis will not return $T$ to its original position.)
(A) $12$ (B) $15$ (C) $17$ (D) $20$ (E) $25$
AMC 10B, 2020, Problem 2
Carl has $5$ cubes each having side length $1$, and Kate has $5$ cubes each having side length $2$. What is the total volume of these $10$ cubes?
(A) $24$ (B) $25$ (C) $28$ (D) $40$ (E) $45$
AMC 10B, 2020, Problem 4
The acute angles of a right triangle are $a^{\circ}$ and $b^{\circ}$, where $a>b$ and both $a$ and $b$ are prime numbers. What is the least possible value of $b$?
(A) $2$ (B) $3$ (C) $5$ (D) $7$ (E) $11$
AMC 10B, 2020, Problem 8
Points $P$ and $Q$ lie in a plane with $PQ=8$. How many locations for point $R$ in this plane are there such that the triangle with vertices $P$, $Q$, and $R$ is a right triangle with area $12$ square units?
(A) $2$ (B) $4$ (C) $6$ (D) $8$ (E) $12$
AMC 10B, 2020, Problem 10
A three-quarter sector of a circle of radius $4$ inches along with its interior is the 2-D net that forms the lateral surface area of a right circular cone by taping together along the two radii shown. What is the volume of the cone in cubic inches?

(A) $3\pi \sqrt5$ (B) $4\pi \sqrt3$ (C) $3 \pi \sqrt7$ (D) $6\pi \sqrt3$ (E) $6\pi \sqrt7$
AMC 10B, 2020, Problem 13
Andy the Ant lives on a coordinate plane and is currently at $(-20, 20)$ facing east (that is, in the positive $x$-direction). Andy moves $1$ unit and then turns $90^{\circ}$ left. From there, Andy moves $2$ units (north) and then turns $90^{\circ}$ left. He then moves $3$ units (west) and again turns $90^{\circ}$ left. Andy continues his progress, increasing his distance each time by $1$ unit and always turning left. What is the location of the point at which Andy makes the $2020$th left turn?
(A) $(-1030, -994)$ (B) $(-1030, -990)$ (C) $(-1026, -994)$ (D) $(-1026, -990)$ (E) $(-1022, -994)$
AMC 10B, 2020, Problem 14
As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length 2 so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded region — inside the hexagon but outside all of the semicircles?

(A) $6\sqrt{3}-3\pi$ (B) $ \frac{9\sqrt{3}}{2} - 2\pi$ (C) $\frac{3\sqrt{3}}{2} - \frac{\pi}{3}$ (D) $3\sqrt{3} - \pi$ (E) $\frac{9\sqrt{3}}{2} - \pi$
AMC 10B, 2020, Problem 21
In square $ABCD$, points $E$ and $H$ lie on $\overline{AB}$ and $\overline{DA}$, respectively, so that $AE=AH.$ Points $F$ and $G$ lie on $\overline{BC}$ and $\overline{CD}$, respectively, and points $I$ and $J$ lie on $\overline{EH}$ so that $\overline{FI} \perp \overline{EH}$ and $\overline{GJ} \perp \overline{EH}$. See the figure below. Triangle $AEH$, quadrilateral $BFIE$, quadrilateral $DHJG$, and pentagon $FCGJI$ each has area $1.$ What is $FI^2$?

(A) $\frac{7}{3}$ (B) $8-4\sqrt2$ (C) $1+ \sqrt2$ (D) $\frac{7}{4}\sqrt2$ (E) $2\sqrt2$
AMC 10B, 2020, Problem 23
Square $ABCD$ in the coordinate plane has vertices at the points $A(1,1), B(-1,1), C(-1,-1),$ and $D(1,-1).$ Consider the following four transformations:
Each of these transformations maps the squares onto itself, but the positions of the labeled vertices will change. For example, applying $R$ and then $V$ would send the vertex $A$ at $(1,1)$ to $(-1,-1)$ and would send the vertex $B$ at $(-1,1)$ to itself. How many sequences of $20$ transformations chosen from $\{L, R, H, V\}$ will send all of the labeled vertices back to their original positions? (For example, $R, R, V, H$ is one sequence of $4$ transformations that will send the vertices back to their original positions.)
(A) $2^{37}$ (B) $3 \cdot 2^{36}$ (C) $2^{38}$ (D) $3 \cdot 2^{37}$ (E) $2^{39}$
AMC 10A, 2019, Problem 6
For how many of the following types of quadrilaterals does there exist a point in the plane of the quadrilateral that is equidistant from all four vertices of the quadrilateral?
(A) $1$ (B) $2$ (C) } $3$ (D) $4$ (E) $5$
AMC 10A, 2019, Problem 7
Two lines with slopes $\frac{1}{2}$ and $2$ intersect at $(2,2)$. What is the area of the triangle enclosed by these two lines and the line $x+y=10 ?$
(A) $4$ (B) $4\sqrt{2}$ (C) $6$ (D) $8$ (E) $6\sqrt{2}$
AMC 10A, 2019, Problem 8
The figure below shows line $l$ with a regular, infinite, recurring pattern of squares and line segments.

How many of the following four kinds of rigid motion transformations of the plane in which this figure is drawn, other than the identity transformation, will transform this figure into itself?
(A) $0$ (B) $1$ (C) $2$ (D) $3$ (E) $4$
AMC 10A, 2019, Problem 10
A rectangular floor that is $10$ feet wide and $17$ feet long is tiled with $170$ one-foot square tiles. A bug walks from one corner to the opposite corner in a straight line. Including the first and the last tile, how many tiles does the bug visit?
(A) $17$ (B) $25$ (C) $26$ (D) $27$ (E) $ 28$
AMC 10A, 2019, Problem 13
Let $\triangle ABC$ be an isosceles triangle with $BC = AC$ and $\angle ACB = 40^{\circ}$. Construct the circle with diameter $\overline{BC}$, and let $D$ and $E$ be the other intersection points of the circle with the sides $\overline{AC}$ and $\overline{AB}$, respectively. Let $F$ be the intersection of the diagonals of the quadrilateral $BCDE$. What is the degree measure of $\angle BFC ?$
(A) $90$ (B) $100$ (C) $105$ (D) $110$ (E) $120$
AMC 10A, 2019, Problem 16
The figure below shows $13$ circles of radius $1$ within a larger circle. All the intersections occur at points of tangency. What is the area of the region, shaded in the figure, inside the larger circle but outside all the circles of radius $1 ?$

(A) $4 \pi \sqrt{3}$ (B) $7\pi$ (C) $ \pi\left(3 \sqrt{3} +2\right)$ (D) $10 \pi \left(\sqrt{3} - 1 \right)$ (E) $\pi \left(\sqrt{3} + 6\right)$
AMC 10A, 2019, Problem 17
A child builds towers using identically shaped cubes of different colors. How many different towers with a height $8$ cubes can the child build with $2$ red cubes, $3$ blue cubes, and $4$ green cubes? (One cube will be left out.)
(A) $24$ (B) $288$ (C) $312$ (D) $1,260$ (E) $40,320$
AMC 10A, 2019, Problem 21
A sphere with center $O$ has radius $6$. A triangle with sides of length $15$, $15$, and $24$ is situated in space so that each of its sides are tangent to the sphere. What is the distance between $O$ and the plane determined by the triangle?
(A) $2\sqrt{3}$ (B) $4$ (C) $3\sqrt{2}$ (D) $2\sqrt{5}$ (E) $5$
AMC 10B, 2019, Problem 4
All lines with equation $ax+by=c$ such that $a,b,c$ form an arithmetic progression pass through a common point. What are the coordinates of that point?
(A) $(-1,2)$ (B) $(0,1)$ (C) $(1,-2)$ (D) $(1,0)$ (E) $(1,2)$
AMC 10B, 2019, Problem 5
Triangle $ABC$ lies in the first quadrant. Points $A$, $B$, and $C$ are reflected across the line $y=x$ to points $A'$,$B'$, and $C'$,respectively. Assume that none of the vertices of the triangle lie on the line $y=x$. Which of the following statements is not always true?
(A) Triangle $A'B'C'$ lies in the first quadrant.
(B) Triangles $ABC$ and $A'B'C'$ have the same area.
(C) The slope of line $AA'$ is $-1$.
(D) The slopes of lines $AA'$ and $CC'$ are the same.
(E) Lines $AB$ and $A'B'$ are perpendicular to each other
AMC 10B, 2019, Problem 8
In triangle $ABC$, point $D$ divides side $\overline{AC}$ so that $AD:DC=1:2$. Let $E$ be the midpoint of $\overline{BD}$ and let $F$ be the point of intersection of line $BC$ and line $AE$. Given that the area of $\triangle ABC$ is $360$, what is the area of $\triangle EBF$?
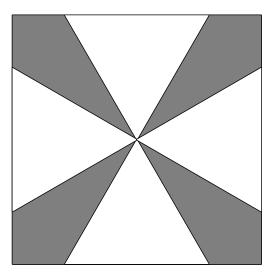
(A) $4$ (B) $12 - 4\sqrt{3}$ (C) $3\sqrt{3}$ (D) $4\sqrt{3}$ (E) $16 - 4\sqrt{3}$
AMC 10B, 2019, Problem 10
In a given plane, points $A$ and $B$ are $10$ units apart. How many points $C$ are there in the plane such that the perimeter of $\triangle ABC$ is $50$ units and the area of $\triangle ABC$ is $100$ square units?
(A) $0$(B) $2$ (C) $4$ (D) $8$ (E) $\text{infinitely many}$
AMC 10B, 2019, Problem 15
Right triangles $T_1$ and $T_2$ have areas 1 and 2, respectively. A side of $T_1$ is congruent to a side of $T_2$, and a different side of $T_1$ is congruent to a different side of $T_2$. What is the square of the product of the other (third) sides of $T_1$ and $T_2$?
(A) $\frac{28}{3}$ (B) $10$ (C) $\frac{32}{3}$ (D) $\frac{34}{3}$ (E) $12$
AMC 10B, 2019, Problem 16
In $\triangle ABC$ with a right angle at $C,$ point $D$ lies in the interior of $\overline{AB}$ and point $E$ lies in the interior of $\overline{BC}$ so that $AC=CD,$ $DE=EB,$ and the ratio $AC:DE=4:3.$ What is the ratio $AD:DB?$
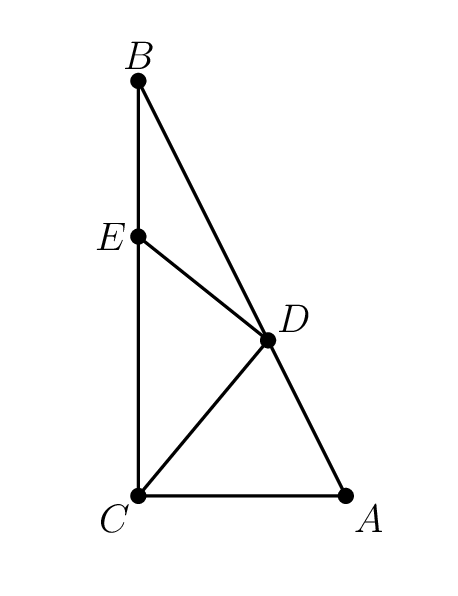
(A) $2:3$ (B) $2\sqrt{5}$ (C) $1:1$ (D) $3\sqrt{5}$ (E) $3:2$
AMC 10B, 2019, Problem 20
As shown in the figure, line segment $\overline{AD}$ is trisected by points $B$ and $C$ so that $AB=BC=CD=2$. Three semicircles of radius $1$,$\overparen{AEB},\overparen{BFC},$ and $\overparen{CGD}$ , have their diameters on $\overline{AD}$, and are tangent to line $EG$ at $E,F,$ and $G,$ respectively. A circle of radius $2$ has its center on $F.$ The area of the region inside the circle but outside the three semicircles, shaded in the figure, can be expressed in the form $ \frac{a}{b}\cdot \pi- \sqrt{c}+d,$ where $a,b,c,$ and $d$ are positive integers and $a$ and $b$ are relatively prime. What is $a+b+c+d$?
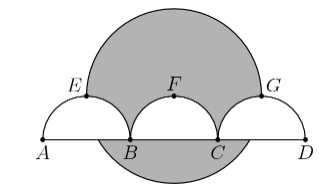
(A) } $13$ (B) $14$ (C) $15$ (D) $16$ (E) $17$
AMC 10B, 2019, Problem 23
Points $A(6,13)$ and $B(12,11)$ lie on circle $\omega$ in the plane. Suppose that the tangent lines to $\omega$ at $A$ and $B$ intersect at a point on the $x$-axis. What is the area of $\omega$?
(A) $\frac{83\pi}{8}$ (B) $\frac{21\pi}{2}$ (C) $ \frac{85\pi}{8}$ (D) $\frac{43\pi}{4}$ (E) $\frac{87\pi}{8}$
AMC 10A, 2018, Problem 9
All of the triangles in the diagram below are similar to isosceles triangle $ABC$, in which $AB=AC$. Each of the $7$ smallest triangles has area $1$, and $\triangle ABC$ has area $40$. What is the area of trapezoid $DBCE$?

(A) $16$ (B) $184 (C) $20$ (D) $22$ (E) $24$
AMC 10A, 2018, Problem 13
A paper triangle with sides of lengths $3, 4$, and $5$ inches, as shown, is folded so that point $A$ falls on point $B$. What is the length in inches of the crease?
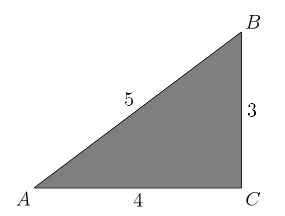
(A) $1+\frac{1}{2}\sqrt2$ (B) $\sqrt3$ (C) $\frac{7}{4}$ (D) $\frac{15}{8}$ (E) $2$
AMC 10A, 2018, Problem 15
Two circles of radius $5$ are externally tangent to each other and are internally tangent to a circle of radius $13$ at points $A$ and $B$, as shown in the diagram. The distance $AB$ can be written in the form $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. What is $m+n$?
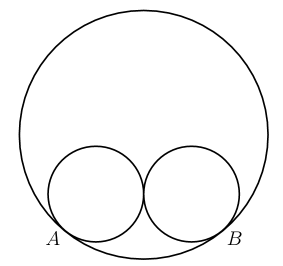
(A) $21$ (B) $29$ (C) $58$ (D) $69$ (E) $93$
AMC 10A, 2018, Problem 16
Right triangle $ABC$ has leg lengths $AB=20$ and $BC=21$. Including $\overline{AB}$ and $\overline{BC}$, how many line segments with integer length can be drawn from vertex $B$ to a point on hypotenuse $\overline{AC}$?
(A) $5$ (B) $8$ (C) $12$ (D) $13$ (E) $15$
AMC 10A, 2018, Problem 20
A scanning code consists of a $7 \times 7$ grid of squares, with some of its squares colored black and the rest colored white. There must be at least one square of each color in this grid of $49$ squares. A scanning code is called $\text{symmetric}$ if its look does not change when the entire square is rotated by a multiple of $90 ^{\circ}$ counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?
(A) $510$ (B) $1022$ (C) $8190$ (D) $8192$ (E) $65,534$
AMC 10A, 2018, Problem 23
Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths $3$ and $4$ units. In the corner where those sides meet at a right angle,he leaves a small unplanted square $S$ so that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from $S$ to the hypotenuse is $2$ units. What fraction of the field is planted?

(A) $ \frac{25}{27}$ (B) $ \frac{26}{27}$ (C) $\frac{73}{75}$ (D) $ \frac{145}{147}$ (E) $ \frac{74}{75}$
AMC 10A,2018,Problem 24
Triangle $ABC$ with $AB=50$ and $AC=10$ has area $120$. Let $D$ be the midpoint of $\overline{AB}$,and let $E$ be the midpoint of $\overline{AC}$. The angle bisector of $\angle BAC$ intersects $\overline{DE}$ and $\overline{BC}$ at $F$ and $G$,respectively. What is the area of quadrilateral $FDBG$?
(A) $60$ (B) $65$ (C) $70$ (D) $75$ (E) $80 $
AMC 10B,2018,Problem 4
A three-dimensional rectangular box with dimensions $X$,$Y$,and $Z$ has faces whose surface areas are $24,24,48,48,72,$ and $72$ square units. What is $X+Y+Z$?
(A) $18 $(B) $22$ (C) $24$ (D) $30$ (E) $36$
AMC 10B,2018,Problem 7
In the figure below,$N$ congruent semicircles are drawn along a diameter of a large semicircle,with their diameters covering the diameter of the large semicircle with no overlap. Let $A$ be the combined area of the small semicircles and $B$ be the area of the region inside the large semicircle but outside the small semicircles. The ratio $A:B$ is $1:18$. What is $N$?

(A) $16$ (B) $17$ (C) $18$ (D) $19$ (E) $36$
AMC 10B,2018,Problem 10
In the rectangular parallelepiped shown,$AB=3$,$BC=1$,and $CG=2$. Point $M$ is the midpoint of $\overline{FG}$. What is the volume of the rectangular pyramid with base $BCHE$ and apex $M$?

(A) $1$ (B) $\frac{4}{3}$ (C) $\frac{3}{2}$ (D) $\frac{5}{3}$ (E) $2$
AMC 10B,2018,Problem 12
Line segment $\overline{AB}$ is a diameter of a circle with $AB=24$. Point $C$,not equal to $A$ or $B$,lies on the circle. As point $C$ moves around the circle,the centroid (center of mass) of $\triangle{ABC}$ traces out a closed curve missing two points. To the nearest positive integer,what is the area of the region bounded by this curve?
(A) $25$ (B) $38$ (C) $50$ (D) $63$ (E) $75$
AMC 10B,2018,Problem 15
A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper,as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box,point $A$ in the figure on the right. The box has base length $w$ and height $h$. What is the area of the sheet of wrapping paper?

(A) $2(w+h)^2$ (B) $ \frac{(w+h)^2}2$ (C) $2w^2+4wh$ (D) $2w^2$ (E) $ w^2h$
AMC 10B,2018,Problem 17
In rectangle $PQRS$,$PQ=8$ and $QR=6$. Points $A$ and $B$ lie on $\overline{PQ}$,points $C$ and $D$ lie on $\overline{QR}$,points $E$ and $F$ lie on $\overline{RS}$,and points $G$ and $H$ lie on $\overline{SP}$ so that $AP=BQ<4$ and the convex octagon $ABCDEFGH$ is equilateral. The length of a side of this octagon can be expressed in the form $k+m\sqrt{n}$,where $k$,$m$,and $n$ are integers and $n$ is not divisible by the square of any prime. What is $k+m+n$?
(A) $1$ (B) $7$ (C) $21$ (D) $92$ (E) $106$
AMC 10B,2018,Problem 24
Let $ABCDEF$ be a regular hexagon with side length $1$. Denote by $X$,$Y$,and $Z$ the midpoints of sides $\overline{AB}$,$\overline{CD}$,and $\overline{EF}$,respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of $\triangle ACE$ and $\triangle XYZ$?
(A) $\frac{3}{8}\sqrt{3}$ (B) $\frac{7}{16}\sqrt{3}$ (C) $\frac{15}{32}\sqrt{3}$ (D) $\frac{1}{2}\sqrt{3}$ (E) $\frac{9}{16}\sqrt{3}$
AMC 10A,2017,Problem 3
Amara has three rows of two $6$-feet by $2$-feet flower beds in her garden. The beds are separated and also surrounded by $1$-foot-wide walkways,as shown on the diagram. What is the total area of the walkways,in square feet?
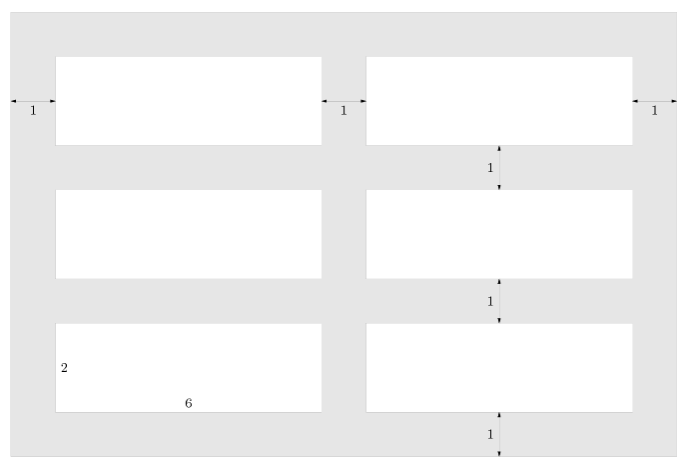
(A) $72$ (B) $78$ (C) $90$ (D) $120$ (E) $150$
AMC 10A,2017,Problem 11
The region consisting of all points in three-dimensional space within $3$ units of line segment $\overline{AB}$ has volume $216\pi$. What is the length $\textit{AB}$?
(A) $6$ (B) $12$ (C) $18$ (D) $20$ (E) $24$
AMC 10A,2017,Problem 12
Let $S$ be a set of points $(x,y)$ in the coordinate plane such that two of the three quantities $3,x+2,$ and $y-4$ are equal and the third of the three quantities is no greater than this common value. Which of the following is a correct description for $S?$
(A) a single point (B) two intersecting lines (C) three lines whose pairwise intersections are three distinct points (D) a triangle
(E) three rays with a common end point
AMC 10A,2017,Problem 17
Distinct points $P$,$Q$,$R$,$S$ lie on the circle $x^2+y^2=25$ and have integer coordinates. The distances $PQ$ and $RS$ are irrational numbers. What is the greatest possible value of the ratio $\frac{PQ}{RS}$?
(A) $3$ (B) $5$ (C) $3\sqrt{5}$ (D) $7$ (E) $5\sqrt{2}$
AMC 10A,2017,Problem 21
A square with side length $x$ is inscribed in a right triangle with sides of length $3$,$4$,and $5$ so that one vertex of the square coincides with the right-angle vertex of the triangle. A square with side length $y$ is inscribed in another right triangle with sides of length $3$,$4$,and $5$ so that one side of the square lies on the hypotenuse of the triangle. What is $\frac{x}{y}$?
(A) $\frac{12}{13}$ (B) $\frac{35}{37}$ (C) $1$ (D) $\frac{37}{35}${(E) $\frac{13}{12}$
AMC 10A,2017,Problem 22
Sides $\overline{AB}$ and $\overline{AC}$ of equilateral triangle $ABC$ are tangent to a circle at points $B$ and $C$ respectively. What fraction of the area of $\triangle ABC$ lies outside the circle?
(A) $\frac{4\sqrt{3}\pi}{27}-\frac{1}{3}$ (B) $\frac{\sqrt{3}}{2}-\frac{\pi}{8}$ (C) $\frac{1}{2}$ (D) $\sqrt{3}-\frac{2\sqrt{3}\pi}{9}$ (E) $\frac{4}{3}-\frac{4\sqrt{3}\pi}{27}$
AMC 10A,2017,Problem 23
How many triangles with positive area have all their vertices at points $(i,j)$ in the coordinate plane,where $i$ and $j$ are integers between $1$ and $5$,inclusive?
(A) $2128$ (B) $2148$ (C) $2160$ (D) $2200$ (E) $2300$
AMC 10B,2017,Problem 6
What is the largest number of solid $2\text{in.}\times 2\text{in.}\times 1\text{in.}$ blocks that can fit in a $3\text{in.}\times 2\text{in.}\times 3\text{in.}$ box?
(A) $3$ (B) $4$ (C) $5$ (D) $6$ (E) $7$
AMC 10B,2017,Problem 8
Points $A(11,9)$ and $B(2,-3)$ are vertices of $\triangle ABC$ with $AB=AC$. The altitude from $A$ meets the opposite side at $D(-1,3)$. What are the coordinates of point $C$?
(A) $(-8,9)$ (B) $(-4,8)$ (C) $(-4,9)$ (D) $(-2,3)$ (E) $(-1,0)$
AMC 10B,2017,Problem 10
The lines with equations $ax-2y=c$ and $2x+by=-c$ are perpendicular and intersect at $(1,-5)$. What is $c$?
(A) $-13$ (B) $-8$ (C) $2$ (D) $8$ (E) $13$
AMC 10B,2017,Problem 15
Rectangle $ABCD$ has $AB=3$ and $BC=4$. Point $E$ is the foot of the perpendicular from $B$ to diagonal $\overline{AC}$. What is the area of $\triangle AED$?
(A) $1$ (B) $\frac{42}{25}$ (C) $\frac{28}{15}$ (D)$ 2$ (E) $\frac{54}{25}$
AMC 10B,2017,Problem 19
Let $ABC$ be an equilateral triangle. Extend side $\overline{AB}$ beyond $B$ to a point $B'$ so that $BB'=3AB$. Similarly,extend side $\overline{BC}$ beyond $C$ to a point $C'$ so that $CC'=3BC$,and extend side $\overline{CA}$ beyond $A$ to a point $A'$ so that $AA'=3CA$. What is the ratio of the area of $\triangle A'B'C'$ to the area of $\triangle ABC$?
(A) $9:1$ (B) $16:1$ (C) $25:1$ (D) $36:1$ (E) $37:1$
AMC 10B, 2017, Problem 21
The diameter $AB$ of a circle of radius $2$ is extended to a point $D$ outside the circle so that $BD=3$. Point $E$ is chosen so that $ED=5$ and line $ED$ is perpendicular to line $AD$. Segment $AE$ intersects the circle at a point $C$ between $A$ and $E$. What is the area of $\triangle ABC$?
(A) $\frac{120}{37}$ (B) $\frac{140}{39}$ (C) $\frac{145}{39}$ (D) $\frac{140}{37}$ (E) $\frac{120}{31}$
AMC 10B, 2017, Problem 24
The vertices of an equilateral triangle lie on the hyperbola $xy=1$, and a vertex of this hyperbola is the centroid of the triangle. What is the square of the area of the triangle?
(A) $48$ (B) $60$ (C) $108$ (D) $120$ (E) $169$
AMC 10A, 2016, Problem 5
A rectangular box has integer side lengths in the ratio $1: 3: 4$. Which of the following could be the volume of the box?
(A) $48$ (B) $56$ (C) $64$ (D) $96$ (E) $144$
AMC 10A, 2016, Problem 10
A rug is made with three different colors as shown. The areas of the three differently colored regions form an arithmetic progression. The inner rectangle is one foot wide, and each of the two shaded regions is $1$ foot wide on all four sides. What is the length in feet of the inner rectangle?

(A) $1$ (B) $2$ (C) $4$ (D) $6$ (E) $8$
AMC 10A, 2016, Problem 11
Find the area of the shaded region.
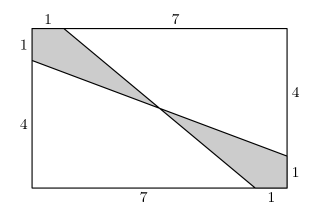
(A) $4\frac{3}{5}$ (B) $5$ (C) $5\frac{1}{4}$ (D)$ 6\frac{1}{2}$ (E) $8$
AMC 10A, 2016, Problem 15
Seven cookies of radius $1$ inch are cut from a circle of cookie dough, as shown. Neighboring cookies are tangent, and all except the center cookie are tangent to the edge of the dough.
The leftover scrap is reshaped to form another cookie of the same thickness. What is the radius in inches of the scrap cookie?
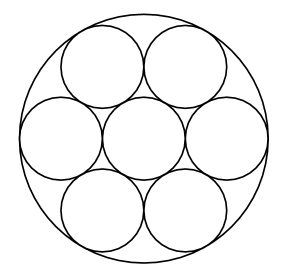
(A) $\sqrt{2}$ (B) $1.5$ (C) $\sqrt{\pi}$ (D) $\sqrt{2\pi}$ (E) $\pi$
AMC 10A, 2016, Problem 16
A triangle with vertices $A(0, 2)$, $B(-3, 2)$, and $C(-3, 0)$ is reflected about the $x$-axis, then the image $\triangle A'B'C'$ is rotated counterclockwise about the origin by $90^{\circ}$ to produce $\triangle A''B''C''$.
Which of the following transformations will return $\triangle A''B''C''$ to $\triangle ABC$?
(A) counterclockwise rotation about the origin by $90^{\circ}$.
(B) clockwise rotation about the origin by $90^{\circ}$.
(C) reflection about the $x$-axis
(D) reflection about the line $y=x$
(E) reflection about the $y$-axis.
AMC 10A,2016,Problem 18
Each vertex of a cube is to be labeled with an integer $1$ through $8$,with each integer being used once,in such a way that the sum of the four numbers on the vertices of a face is the same for each face. Arrangements that can be obtained from each other through rotations of the cube are considered to be the same. How many different arrangements are possible?
(A) $1$ (B) $3$ (C) $6$ (D) $12$ (E) $24$
AMC 10A,2016,Problem 19
In rectangle $ABCD,$ $AB=6$ and $BC=3$. Point $E$ between $B$ and $C$,and point $F$ between $E$ and $C$ are such that $BE=EF=FC$. Segments $\overline{AE}$ and $\overline{AF}$ intersect $\overline{BD}$ at $P$ and $Q$,respectively. The ratio $BP:PQ:QD$ can be written as $r:s:t$ where the greatest common factor of $r,s$ and $t$ is $1$. What is $r+s+t$?
(A) $7$ (B) $9$ (C) $12$ (D) $15$ (E) $20$
AMC 10A,2016,Problem 21
Circles with centers $P,Q$ and $R$,having radii $1,2$ and $3$,respectively,lie on the same side of line $l$ and are tangent to $l$ at $P', Q'$ and $R'$, respectively, with $Q'$ between $P'$ and $R'$.
The circle with center $Q$ is externally tangent to each of the other two circles. What is the area of triangle $PQR$?
(A) $0$ (B) $\sqrt{\frac{2}{3}}$ (C) $1$ (D) $\sqrt{6}-\sqrt{2}$ (E) $\sqrt{\frac{3}{2}}$
AMC 10A,2016,Problem 24
A quadrilateral is inscribed in a circle of radius $200\sqrt{2}$. Three of the sides of this quadrilateral have length $200$. What is the length of the fourth side?
(A) $200$ (B) $200\sqrt{2}$ (C) $200\sqrt{3}$ (D) $300\sqrt{2}$ (E) $500$
AMC 10B,2016,Problem 7
The ratio of the measures of two acute angles is $5:4$,and the complement of one of these two angles is twice as large as the complement of the other.
What is the sum of the degree measures of the two angles?
(A) $75$ (B) $90$ (C) $135$ (D) $150$ (E) $270$
AMC 10B,2016,Problem 9
All three vertices of $\bigtriangleup ABC$ are lying on the parabola defined by $y=x^2$,with $A$ at the origin and $\overline{BC}$ parallel to the $x$-axis. The area of the triangle is $64$. What is the length of $BC$?
(A) $4$ (B) $6$ (C) $8$ (D) $10$(E) $16$
AMC 10B,2016,Problem 10
A thin piece of wood of uniform density in the shape of an equilateral triangle with side length $3$ inches weighs $12$ ounces. A second piece of the same type of wood,with the same thickness,also in the shape of an equilateral triangle,has side length of $5$ inches.
Which of the following is closest to the weight,in ounces,of the second piece?
(A) $14.0$ (B) $16.0$ (C) $20.0$ (D) $33.3$ (E) $55.6$
AMC 10B,2016,Problem 11
Carl decided to fence in his rectangular garden. He bought $20$ fence posts,placed one on each of the four corners,and spaced out the rest evenly along the edges of the garden,leaving exactly $4$ yards between neighboring posts.
The longer side of his garden,including the corners,has twice as many posts as the shorter side,including the corners. What is the area,in square yards,of Carl’s garden?
(A) $256$ (B) $336$ (C) $384$ (D) $448$ (E) $512$
AMC 10B,2016,Problem 14
How many squares whose sides are parallel to the axis and whose vertices have coordinates that are integers lie entirely within the region bounded by the line $y=\pi x$,the line $y=-0.1$ and the line $x=5.1?$
(A) $30$ (B) $41$ (C)$45$ (D) $50$ (E) $57$
AMC 10B,2016,Problem 15
All the numbers $1,2,3,4,5,6,7,8,9$ are written in a $3\times 3$ array of squares,one number in each square,in such a way that if two numbers are consecutive then they occupy squares that share an edge. The numbers in the four corners add up to $18$. What is the number in the center?
(A) $5$ (B) $6$ (C) $7$ (D) $8$ (E) $9$
AMC 10B,2016,Problem 17
All the numbers $2,3,4,5,6,7$ are assigned to the six faces of a cube,one number to each face. For each of the eight vertices of the cube,a product of three numbers is computed,where the three numbers are the numbers assigned to the three faces that include that vertex.
What is the greatest possible value of the sum of these eight products?
(A) $312$ (B) $343$ (C) $625$ (D) $729$ (E) $1680$
AMC 10B,2016,Problem 19
Rectangle $ABCD$ has $AB=5$ and $BC=4$. Point $E$ lies on $\overline{AB}$ so that $EB=1$,point $G$ lies on $\overline{BC}$ so that $CG=1$. and point $F$ lies on $\overline{CD}$ so that $DF=2$.
Segments $\overline{AG}$ and $\overline{AC}$ intersect $\overline{EF}$ at $Q$ and $P$,respectively. What is the value of $\frac{PQ}{EF}$?

(A) $\frac{\sqrt{13}}{16}$ (B) $\frac{\sqrt{2}}{13}$ (C)$\frac{9}{82}$ (D)$\frac{10}{91}$(E)$\frac{1}{9}$
AMC 10B,2016,Problem 20
A dilation of the plane—that is,a size transformation with a positive scale factor—sends the circle of radius $2$ centered at $A(2,2)$ to the circle of radius $3$ centered at $A’(5,6)$. What distance does the origin $O(0,0)$,move under this transformation?
(A)$0$ (B) $3$ (C)$\sqrt{13}$ (D)$ 4$ (E) $5$
AMC 10B,2016,Problem 21
What is the area of the region enclosed by the graph of the equation $x^2+y^2=|x|+|y|?$
(A)$\pi+\sqrt{2}$ (B)$\pi+2$ (C)$\pi+2\sqrt{2}$ (D) $2\pi+\sqrt{2}$ (E) $2\pi+2\sqrt{2}$
AMC 10B,2016,Problem 23
In regular hexagon $ABCDEF$,points $W$,$X$,$Y$,and $Z$ are chosen on sides $\overline{BC}$,$\overline{CD}$,$\overline{EF}$,and $\overline{FA}$ respectively,so lines $AB$,$ZW$,$YX$,and $ED$ are parallel and equally spaced. What is the ratio of the area of hexagon $WCXYFZ$ to the area of hexagon $ABCDEF$?
(A) $\frac{1}{3}$ (B)$\frac{10}{27}$ (C)$\frac{11}{27}$ (D)$\frac{4}{9}$ (E)$\frac{13}{27}$
AMC 10A,2015,Problem 11
The ratio of the length to the width of a rectangle is $4$ :$3$. If the rectangle has diagonal of length $d$,then the area may be expressed as $kd^2$ for some constant $k$. What is $k$?
(A) $\frac{2}{7}$ (B)$\frac{3}{7}$ (C)$\frac{12}{25}$ (D)$\frac{16}{25}$ (E)$\frac{3}{4}$
AMC 10A,2015,Problem 12
Points $(\sqrt{\pi},a)$ and $(\sqrt{\pi},b)$ are distinct points on the graph of $y^2+x^4=2x^2y+1$. What is $|a-b|$?
(A) $1$ (B) $\frac{\pi}{2}$ (C) $2$ (D) $\sqrt{1+\pi}$ (E) $1+\sqrt{\pi}$
AMC 10A,2015,Problem 17
A line that passes through the origin intersects both the line $x=1$ and the line $y=1+\frac{\sqrt{3}}{3}x$. The three lines create an equilateral triangle. What is the perimeter of the triangle?
(A) $2\sqrt{6}$ (B) $2+2\sqrt{3}$ (C) $6$ (D) $3+2\sqrt{3}$ (E) $6+\frac{\sqrt{3}}{3}$
AMC 10A,2015,Problem 19
The isosceles right triangle $ABC$ has right angle at $C$ and area $12.5$.
The rays trisecting $\angle ACB$ intersect $AB$ at $D$ and $E$. What is the area of $\bigtriangleup CDE$?
(A) $\frac{5\sqrt{2}}{3}$
(B) $\frac{50\sqrt{3}-75}{4}$
(C) $\frac{15\sqrt{3}}{8}$
(D) $\frac{50-25\sqrt{3}}{2}$
(E) $\frac{25}{6}$
AMC 10A,2015,Problem 21
Tetrahedron $ABCD$ has $AB=5$,$AC=3$,$BC=4$,$BD=4$,$AD=3$,and $CD=\frac{1}{2}5\sqrt{2}$.
What is the volume of the tetrahedron?
(A) $3\sqrt2$ (B) $2\sqrt5$ (C) $\frac{24}{5}$ (D) $3\sqrt3$
(E) $\frac{24}{5}\sqrt2$
AMC 10A,2015,Problem 24
For some positive integers $p$,there is a quadrilateral $ABCD$ with positive integer side lengths,perimeter $p$,right angles at $B$ and $C$,$AB=2$,and $CD=AD$.
How many different values of $p<2015$ are possible?
(A) $30$ (B) $31$ (C) $61$(D) $62$ (E) $63$
AMC 10A,2015,Problem 25
Let $S$ be a square of side length $1$. Two points are chosen at random on the sides of $S$. The probability that the straight-line distance between the points is at least $\frac{1}{2}$ is $\frac{a-b\pi}c$,where $a$,$b$,and $c$ are positive integers with $gcd(a,b,c)=1$. What is $a+b+c$?
(A) $59$(B) $60$ (C) $61$ (D) $62$ (E) $63$
AMC 10B,2015,Problem 8
The letter F shown below is rotated $90^{\circ}$ clockwise around the origin,then reflected in the $y$-axis,and then rotated a half turn around the origin. What is the final image?
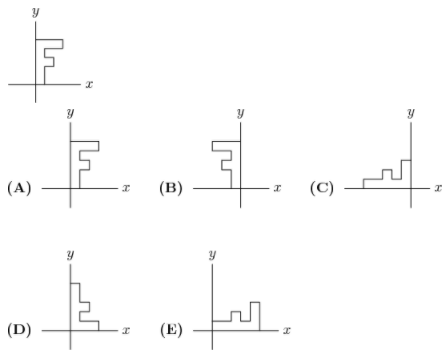
AMC 10B,2015,Problem 9
The shaded region below is called a shark's fin falcata, a figure studied by Leonardo da Vinci. It is bounded by the portion of the circle of radius 3 and center $(0,0)$ that lies in the first quadrant, the portion of the circle with radius $\frac{3}{2}$ and center $\left(0, \frac{3}{2}\right)$ that lies in the first quadrant, and the line segment from $(0,0)$ to $(3,0)$. What is the area of the shark's fin falcata?

(A) $\frac{4 \pi}{5}$
(B) $\frac{9 \pi}{8}$
(C) $\frac{4 \pi}{3}$
(D) $\frac{7 \pi}{5}$
(E) $\frac{3 \pi}{2}$
AMC 10B,2015,Problem 13
The line $12x+5y=60$ forms a triangle with the coordinate axes. What is the sum of the lengths of the altitudes of this triangle?
(A) $20$ (B) $\frac{360}{17}$ (C) $\frac{107}{5}$ (D) $\frac{43}{2}$ (E) $\frac{281}{13}$
AMC 10B,2015,Problem 17
The centers of the faces of the right rectangular prism shown below are joined to create an octahedron,what is the volume of the octahedron?

(A) $\frac{75}{12}$ (B) $10$ (C) $12$ (D) $10\sqrt2$ (E) $15$
AMC 10B,2015,Problem 19
In $\triangle{ABC}$,$\angle{C}=90^{\circ}$ and $AB=12$. Squares $ABXY$ and $ACWZ$ are constructed outside of the triangle. The points $X,Y,Z$,and $W$ lie on a circle. What is the perimeter of the triangle?
(A) $12+9\sqrt{3}$ (B) $18+6\sqrt{3}$ (C) $12+12\sqrt{2}$(D) $30$ (E) $32$
AMC 10B,2015,Problem 22
In the figure shown below,$ABCDE$ is a regular pentagon and $AG=1$. What is $FG+JH+CD$?

(A) $3$ (B) $12-4\sqrt5$ (C) $\frac{5+2\sqrt5}{3}$ (D) $1+\sqrt5$ (E) $\frac{11+11\sqrt5}{10}$
AMC 10B,2015,Problem 25
A rectangular box measures $a \times b \times c$,where $a,$ $b,$ and $c$ are integers and $1 \leq a \leq b \leq c$. The volume and surface area of the box are numerically equal. How many ordered triples $(a,b,c)$ are possible?
(A) $4$(B) $10$(C) $12$(D) $21$(E) $26$
AMC 10A,2014,Problem 9
The two legs of a right triangle,which are altitudes,have lengths $2\sqrt3$ and $6$. How long is the third altitude of the triangle?
(A) $1$ (B) $2$ (C) $3$(D) $4$(E) $5$
AMC 10A,2014,Problem 12
A regular hexagon has side length $6$. Congruent arcs with radius $3$ are drawn with the center at each of the vertices,creating circular sectors as shown. The region inside the hexagon but outside the sectors is shaded as shown. What is the area of the shaded region?

(A) $27\sqrt{3}-9\pi$ (B) $27\sqrt{3}-6\pi$ (C) $54\sqrt{3}-18\pi$
(D) $54\sqrt{3}-12\pi$ (E) $108\sqrt{3}-9\pi$
AMC 10A,2014,Problem 13
Equilateral $\triangle ABC$ has side length $1$,and squares $ABDE$,$BCHI$,$CAFG$ lie outside the triangle. What is the area of hexagon $DEFGHI$?

(A)$ \frac{12+3\sqrt3}{4}$(B)$ \frac{9}{2}$
(C)$ 3+\sqrt3$(D)$ \frac{6+3\sqrt3}{2}$(E) $6$
AMC 10A,2014,Problem 14
The $y$-intercepts,$P$ and $Q$,of two perpendicular lines intersecting at the point $A(6,8)$ have a sum of zero. What is the area of $\triangle APQ$?
(A) $45$(B)$ 48$(C)$ 54$(D) $60$(E) $72$
AMC 10A,2014,Problem 16
In rectangle $ABCD$,$AB=1$,$BC=2$,and points $E$,$F$,and $G$ are midpoints of $\overline{BC}$,$\overline{CD}$,and $\overline{AD}$,respectively. Point $H$ is the midpoint of $\overline{GE}$. What is the area of the shaded region?

(A)$\frac{1}{12}$ (B)$\frac{\sqrt{3}}{18}$ (C)$\frac{\sqrt{2}}{12}$
(D)$\frac{\sqrt{3}}{12}$ (E)$\frac{1}{6}$
AMC 10A,2014,Problem 18
A square in the coordinate plane has vertices whose $y$-coordinates are $0$,$1$,$4$,and $5$. What is the area of the square?
(A)$16$(B)$ 17$(C) $25$(D)$ 26$(E) $27$
AMC 10A,2014,Problem 19
Four cubes with edge lengths $1$,$2$,$3$,and $4$ are stacked as shown. What is the length of the portion of $\overline{XY}$ contained in the cube with edge length $3$?

(A)$\frac{3\sqrt{33}}{5}$(B)$2\sqrt{3}$(C)$\frac{2\sqrt{33}}{3}$(D)$ 4$(E)$ 3\sqrt{2}$
AMC 10A,2014,Problem 22
In rectangle $ABCD$,$AB=20$ and $BC=10$. Let $E$ be a point on $\overline{CD}$ such that $\angle CBE=15^{\circ}$. What is $AE$?
(A)$\frac{20\sqrt{3}}{3}$(B)$10\sqrt3$(C)$ 18$(D)$11\sqrt3$(E)$ 20$
AMC 10A,2014,Problem 23
A rectangular piece of paper whose length is $\sqrt3$ times the width has area $A$. The paper is divided into three equal sections along the opposite lengths,and then a dotted line is drawn from the first divider to the second divider on the opposite side as shown. The paper is then folded flat along this dotted line to create a new shape with area $B$. What is the ratio $B:A$?

(A)$1:2$(B)$3:5$(C)$ 2:3$(D)$ 3:4$(E)$ 4:5$
AMC 10B,2014,Problem 5
Camden constructs a square window using $8$ equal-size panes of glass,as shown. The ratio of the height to width for each pane is $5 :2$,and the borders around and between the panes are $2$ inches wide. In inches,what is the side length of the square window?

(A)$ 26$(B)$ 28$(C)$ 30$(D)$ 32$(E)$ 34$
AMC 10B,2014,Problem 13
Six regular hexagons surround a regular hexagon of side length $1$ as shown. What is the area of $\triangle ABC$?
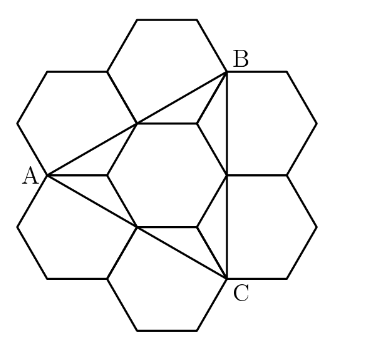
(A) $2\sqrt{3}$ (B) $ 3\sqrt{3}$ (C) $ 1+3\sqrt{2}$(D) $2+2\sqrt{3}$ (E) $ 3+2\sqrt{3}$
AMC 10A,2014,Problem 15
In rectangle $ABCD$,$DC=2CB$ and points $E$ and $F$ lie on $\overline{AB}$ so that $\overline{ED}$ and $\overline{FD}$ trisect $\angle ADC$ as shown. What is the ratio of the area of $\triangle DEF$ to the area of rectangle $ABCD$?

(A)$ \frac{\sqrt{3}}{6}$(B) $\frac{\sqrt{6}}{8}$ (C)$ \frac{3\sqrt{3}}{16}$(D)$ \frac{1}{3}$(E) $\frac{\sqrt{2}}{4}$
AMC 10B,2014,Problem 19
Two concentric circles have radii $1$ and $2$. Two points on the outer circle are chosen independently and uniformly at random. What is the probability that the chord joining the two points intersects the inner circle?
(A) $\frac{1}{6}$ (B) $\frac{1}{4}$(C) $\frac{2-\sqrt{2}}{2}$ (D) $\frac{1}{3}$ (E) $\frac{1}{2}$
AMC 10B,2014,Problem 21
Trapezoid $ABCD$ has parallel sides $\overline{AB}$ of length $33$ and $\overline{CD}$ of length $21$. The other two sides are of lengths $10$ and $14$. The angles at $A$ and $B$ are acute. What is the length of the shorter diagonal of $ABCD$?
(A) $ 10\sqrt{6}$ (B) $25$ (C) $ 8\sqrt{10}$ (D) $ 18\sqrt{2}$ (E) $ 26$
AMC 10B,2014,Problem 22
Eight semicircles line the inside of a square with side length 2 as shown. What is the radius of the circle tangent to all of these semicircles?
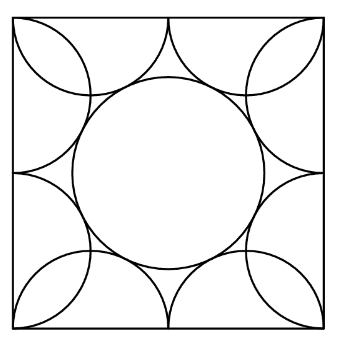
(A) $ \frac{1+\sqrt2}4$ (B) $ \frac{\sqrt5-1}2$ (C) $ \frac{\sqrt3+1}4$ (D) $ \frac{2\sqrt3}5$ (E) $\frac{\sqrt5}3$
AMC 10B,2014,Problem 23
A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?
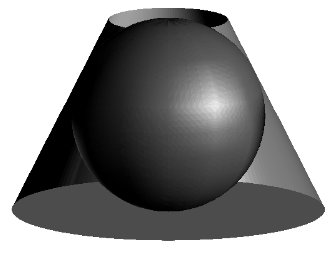
(A) $\frac{3}{2}$ (B) $\frac{1+\sqrt5}2$ (C) $\sqrt3$ (D) $2$ (E) $\frac{3+\sqrt5}2$
AMC 10A,2013,Problem 3
Square $ABCD$ has side length $10$. Point $E$ is on $\overline{BC}$,and the area of $\triangle ABE$ is $40$. What is $BE$?
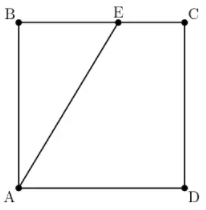
(A)$4$
(B) $5$
(C)$6$
(D)$7$
(E)$8$
AMC 10A,2013,Problem 12
In $\triangle ABC$,$AB=AC=28$ and $BC=20$. Points $D,E,$ and $F$ are on sides $\overline{AB}$,$\overline{BC}$,and $\overline{AC}$,respectively,such that $\overline{DE}$ and $\overline{EF}$ are parallel to $\overline{AC}$ and $\overline{AB}$,respectively. What is the perimeter of parallelogram $ADEF$?
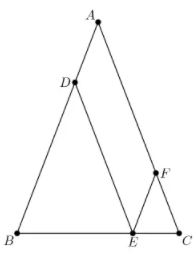
(A) $48$
(B) $52$
(C) $56$
(D) $60$
(E) $72$
AMC 10A,2013,Problem 14
A solid cube of side length $1$ is removed from each corner of a solid cube of side length $3$. How many edges does the remaining solid have?
(A) $36$(B) $60$(C) $72$(D) $84$(E) $108$
AMC 10A,2013,Problem 15
Two sides of a triangle have lengths $10$ and $15$. The length of the altitude to the third side is the average of the lengths of the altitudes to the two given sides. How long is the third side?
(A)$6$ (B) $8$ (C)$9$ (D) $12$ (E) $18$
AMC 10A,2013,Problem 16
A triangle with vertices $(6,5)$,$(8,-3)$,and $(9,1)$ is reflected about the line $x=8$ to create a second triangle. What is the area of the union of the two triangles?
(A)$9$ (B)$\frac{28}{3}$ (C)$ 10$ (D)$\frac{31}{3}$ (E)$\frac{32}{3}$
AMC 10A,2013,Problem 18
Let points $A=(0,0)$,$B=(1,2)$,$C=(3,3)$,and $D=(4,0)$. Quadrilateral $ABCD$ is cut into equal area pieces by a line passing through $A$. This line intersects $\overline{CD}$ at point $(\frac{p}{q},\frac{r}{s})$,where these fractions are in lowest terms. What is $p+q+r+s$?
(A)$54$(B)$58$(C)$62$(D)$70$(E)$75$
AMC 10A,2013,Problem 20
A unit square is rotated $45^{\circ}$ about its center. What is the area of the region swept out by the interior of the square?
(A)$ 1 - \frac{\sqrt{2}}{2}+\frac{\pi}{4}$
(B)$\frac{1}{2}+\frac{\pi}{4}$
(C)$2 - \sqrt{2}+\frac{\pi}{4}$
(D)$\frac{\sqrt{2}}{2}+\frac{\pi}{4}$
(E)$1+\frac{\sqrt{2}}{4}+\frac{\pi}{8}$
AMC 10A,2013,Problem 22
Six spheres of radius $1$ are positioned so that their centers are at the vertices of a regular hexagon of side length $2$. The six spheres are internally tangent to a larger sphere whose center is the center of the hexagon. An eighth sphere is externally tangent to the six smaller spheres and internally tangent to the larger sphere. What is the radius of this eighth sphere?
(A)$\sqrt{2}$
(B)$\frac{3}{2}$
(C)$\frac{5}{3}$
(D)$\sqrt{3}$
(E)$2$
AMC 10A,2013,Problem 23
In $\triangle ABC$,$AB=86$,and $AC=97$. A circle with center $A$ and radius $AB$ intersects $\overline{BC}$ at points $B$ and $X$. Moreover $\overline{BX}$ and $\overline{CX}$ have integer lengths. What is $BC$?
(A)$11$ (B)$28$ (C)$33$ (D)$61$ (E)$72$
AMC 10A,2013,Problem 25
All $20$ diagonals are drawn in a regular octagon. At how many distinct points in the interior of the octagon (not on the boundary) do two or more diagonals intersect?
(A)$49$(B)$65$(C)$70$(D)$96$(E)$128$
AMC 10B,2013,Problem 2
Mr. Green measures his rectangular garden by walking two of the sides and finding that it is $15$ steps by $20$ steps. Each of Mr. Green's steps is $2$ feet long. Mr. Green expects a half a pound of potatoes per square foot from his garden. How many pounds of potatoes does Mr. Green expect from his garden?
(A)$600$ (B) $800$ (C) $1000$ (D) $1200$ (E) $1400$
AMC 10B, 2013, Problem 7
Six points are equally spaced around a circle of radius $1$. Three of these points are the vertices of a triangle that is neither equilateral nor isosceles. What is the area of this triangle?
(A) $\frac{\sqrt{3}}{3}$ (B)$\frac{\sqrt{3}}{2}$(C)$1$ (D)$\sqrt{2}$ (E)$2$
AMC 10B, 2013, Problem 15
A wire is cut into two pieces, one of length $a$ and the other of length $b$. The piece of length $a$ is bent to form an equilateral triangle, and the piece of length $b$ is bent to form a regular hexagon.
The triangle and the hexagon have equal area. What is $\frac{a}{b}$?
(A)$1$ (B)$\frac{\sqrt{6}}{2}$ (C)$\sqrt{3}$ (D) $2$(E)$\frac{3\sqrt{2}}{2}$
AMC 10B, 2013, Problem 16
In triangle $ABC$, medians $AD$ and $CE$ intersect at $P$, $PE=1.5$, $PD=2$, and $DE=2.5$. What is the area of $AEDC$?
(A)$13$(B)$13.5$(C)$14$(D)$14.5$(E)$15$
AMC 10B, 2013, Problem 22
The regular octagon $ABCDEFGH$ has its center at $J$. Each of the vertices and the center are to be associated with one of the digits $1$ through $9$, with each digit used once, in such a way that the sums of the numbers on the lines $AJE$, $BJF$, $CJG$, and $DJH$ are all equal. In how many ways can this be done?

(A)$384$ (B) $576$ (C)$1152$ (D) $1680$ (E) $3456$
AMC 10B, 2013, Problem 23
In triangle $ABC$, $AB = 13$, $BC = 14$, and $CA = 15$. Distinct points $D$, $E$, and $F$ lie on segments $\overline{BC}$, $\overline{CA}$, and $\overline{DE}$, respectively, such that $\overline{AD} \perp \overline{BC}$, $\overline{DE} \perp \overline{AC}$, and $\overline{AF} \perp \overline{BF}$. The length of segment $\overline{DF}$ can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. What is $m + n$?
(A)$18$(B)$21$(C)$24$(D)$27$(E)$30$
AMC 10A, 2012, Problem 2
A square with side length 8 is cut in half, creating two congruent rectangles. What are the dimensions of one of these rectangles?
(A)$2 \text{by} 4$(B)$2 \text{by} 6$(C)$2 \text{by} 8$(D)$4 \text{by} 4$(E)$4 \text{by} 8$
AMC 10A, 2012, Problem 4
Let $\angle ABC = 24^{\circ}$ and $\angle ABD = 20^{\circ}$. What is the smallest possible degree measure for $\angle CBD$?
(A) $0$ (B) $2$(C) $4$(D)$6$(E) $12$
AMC 10A, 2012, Problem 10
Mary divides a circle into $12$ sectors. The central angles of these sectors, measured in degrees, are all integers and they form an arithmetic sequence. What is the degree measure of the smallest possible sector angle?
(A)$5$(B)$6$(C)$8$(D)$10$(E)$12$
AMC 10A, 2012, Problem 11
Mary divides a circle into $12$ sectors. The central angles of these sectors, measured in degrees, are all integers and they form an arithmetic sequence. What is the degree measure of the smallest possible sector angle?
(A)$5$(B)$6$(C)$8$(D)$10$(E)$12$
AMC 10A, 2012, Problem 15
Three unit squares and two line segments connecting two pairs of vertices are shown. What is the area of $\triangle ABC$?

(A)$\frac{1}{6}$ (B)$\frac{1}{5}$ (C) $\frac{2}{9}$ (D)$\frac{1}{3}$ (E)$\frac{\sqrt{2}}{4}$
AMC 10A, 2012, Problem 18
The closed curve in the figure is made up of $9$ congruent circular arcs each of length $\frac{2\pi}{3}$, where each of the centers of the corresponding circles is among the vertices of a regular hexagon of side $2$. What is the area enclosed by the curve?

(A)$2\pi+6$(B)$2\pi+4\sqrt{3}$(C)$3\pi+4$(D) $2\pi+3\sqrt{3}+2$(E)$\pi+6\sqrt{3}$
AMC 10A, 2012, Problem 21
Let points $A = (0 ,0 ,0)$, $B = (1, 0, 0)$, $C = (0, 2, 0)$, and $D = (0, 0, 3)$. Points $E$, $F$, $G$, and $H$ are midpoints of line segments $\overline{BD},\overline{AB}, \overline {AC},$ and $\overline{DC}$ respectively. What is the area of $EFGH$?
(A)$\sqrt{2}$(B)$\frac{2\sqrt{5}}{3}$(C)$\frac{3\sqrt{5}}{4}$(D)$\sqrt{3}$(E)$\frac{2\sqrt{7}}{3}$
AMC 10B, 2012, Problem 2
A circle of radius 5 is inscribed in a rectangle as shown. The ratio of the length of the rectangle to its width is 2:1. What is the area of the rectangle?

(A)$50$(B)$100$(C)$125$(D)$150$(E)$200$
AMC 10B, 2012, Problem 3
The point in the $xy$-plane with coordinates $(1000, 2012)$ is reflected across the line $y = 2000$. What are the coordinates of the reflected point?
(A)$(998,2012)$(B)$(1000,1988)$(C)$(1000,2024)$(D)$(1000,4012)$(E)$(1012,2012)$
AMC 10B, 2012, Problem 14
Two equilateral triangles are contained in a square whose side length is $2\sqrt {3}$.
The bases of these triangles are the opposite sides of the square, and their intersection is a rhombus. What is the area of the rhombus?
(A) $\frac{3}{2}$ (B) $\sqrt {3}$ (C) $2\sqrt {2 - 1}$ (D) $8\sqrt {3 - 12}$ (E)$\frac{4\sqrt {3}}{3}$
AMC 10B, 2012, Problem 16
Three circles with radius $2$ are mutually tangent. What is the total area of the circles and the region bounded by them, as shown in the figure?

(A)$10\pi+4\sqrt{3}$(B)$13\pi-\sqrt{3}$(C)$12\pi+\sqrt{3}$(D)$10\pi+9$(E)$13\pi$
AMC 10B, 2012, Problem 17
Jesse cuts a circular paper disk of radius $12$ along two radii to form two sectors, the smaller having a central angle of $120$ degrees.
He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?
(A)$\frac{1}{8}$(B)$\frac{1}{4}$(C)$\frac{\sqrt{10}}{10}$(D)$\frac{\sqrt{5}}{6}$(E)$\frac{\sqrt{5}}{5}$
AMC 10B, 2012, Problem 19
In rectangle $ABCD$, $AB=6$, $AD=30$, and $G$ is the midpoint of $\overline{AD}$. Segment $AB$ is extended $2$ units beyond $B$ to point $E$, and $F$ is the intersection of $\overline{ED}$ and $\overline{BC}$. What is the area of $BFDG$?
(A)$\frac{133}{2}$(B)$67$(C)$\frac{135}{2}$(D)$68$(E)$\frac{137}{2}$
AMC 10B, 2012, Problem 23
A solid tetrahedron is sliced off a wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?
(A)$\frac{\sqrt{3}}{3}$(B)$\frac{2\sqrt{2}}{3}$(C)$1$(D)$\frac{2\sqrt{3}}{3}$(E)$\sqrt{2}$
AMC 10B, 2012, Problem 25
A bug travels from $A$ to $B$ along the segments in the hexagonal lattice pictured below. The segments marked with an arrow can be traveled only in the direction of the arrow, and the bug never travels the same segment more than once. How many different paths are there?

(A)$2112$(B)$2304$(C)$2368$(D)$2384$(E)$2400$
AMC 10A, 2011, Problem 9
A rectangular region is bounded by the graphs of the equations $y=a, y=-b, x=-c,$ and $x=d$, where $a,b,c,$ and $d$ are all positive numbers. Which of the following represents the area of this region?
(A)$ac+ad+bc+bd$ (B)$ac-ad+bc-bd$(C)$ac+ad -bc-bd$ (D)$-ac-ad+bc+bd$(E)$ac-ad-bc+bd$
AMC 10A, 2011, Problem 11
Square $EFGH$ has one vertex on each side of square $ABCD$. Point $E$ is on $\overline{AB}$ with $AE=7\dot EB$. What is the ratio of the area of $EFGH$ to the area of $ABCD$?
(A)$\frac{49}{64}$(B)$\frac{25}{32}$(C)$\frac{7}{8}$(D)$\frac{5\sqrt{2}}{8}$ (E)$\frac{\sqrt{14}}{4}$
AMC 10A, 2011, Problem 18
Circles $A, B,$ and $C$ each have radius $1$. Circles $A$ and $B$ share one point of tangency. Circle $C$ has a point of tangency with the midpoint of $\overline{AB}$. What is the area inside Circle $C$ but outside circle $A$ and circle $B$ ?
(A)$3 - \frac{\pi}{2}$ (B)$\frac{\pi}{2}$ (C)$2$ (D)$\frac{3\pi}{4}$ (E)$1+\frac{\pi}{2}$
AMC 10A, 2011, Problem 20
Two points on the circumference of a circle of radius $r$ are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?
(A)$\frac{1}{6}$ (B)$\frac{1}{5}$(C)$\frac{1}{4}$(D)$\frac{1}{3}$(E)$\frac{1}{2}$
AMC 10A, 2011, Problem 22
Each vertex of convex pentagon $ABCDE$ is to be assigned a color. There are $6$ colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?
(A)$2520$(B)$2880$(C)$3120$(D)$3250$(E)$3750$
AMC 10A, 2011, Problem 24
Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?
(A)$\frac{1}{12}$(B)$\frac{\sqrt{2}}{12}$(C)$\frac{\sqrt{3}}{12}$(D)$\frac{1}{6}$(E)$\frac{\sqrt{2}}{6}$
AMC 10B, 2011, Problem 3
At a store, when a length is reported as $x$ inches that means the length is at least $x - 0.5$ inches and at most $x + 0.5$ inches. Suppose the dimensions of a rectangular tile are reported as $2$ inches by $3$ inches. In square inches, what is the minimum area for the rectangle?
(A)$3.75$(B)$4.5$(C)$5$(D)$6$(E)$8.75$
AMC 10B, 2011, Problem 7
The sum of two angles of a triangle is $6/5$ of a right angle, and one of these two angles is $30^{\circ}$ larger than the other. What is the degree measure of the largest angle in the triangle?
(A)$69$(B)$72$(C)$90$(D)$102$(E)$108$
AMC 10B, 2011, Problem 9
The area of $\triangle EBD$ is one third of the area of $3-4-5$ $\triangle ABC$. Segment $DE$ is perpendicular to segment $AB$. What is $BD$?

(A)$\frac{4}{3}$(B)$\sqrt{5}$(C)$\frac{9}{4}$(D)$\frac{4\sqrt{3}}{3}$(E)$\frac{5}{2}$
AMC 10B, 2011, Problem 14
A rectangular parking lot has a diagonal of $25$ meters and an area of $168$ square meters. In meters, what is the perimeter of the parking lot?
(A)$52$(B)$58$(C)$62$(D)$68$ (E)$70$
AMC 10B, 2011, Problem 16
A dart board is a regular octagon divided into regions as shown. Suppose that a dart thrown at the board is equally likely to land anywhere on the board. What is probability that the dart lands within the center square?

(A)$\frac{\sqrt{2} - 1}{2}$ (B)$\frac{1}{4}$ (C)$\frac{2 - \sqrt{2}}{2}$
(D)$\frac{\sqrt{2}}{4}$ (E)$2 - \sqrt{2}$
AMC 10B, 2011, Problem 17
In the given circle, the diameter $\overline{EB}$ is parallel to $\overline{DC}$, and $\overline{AB}$ is parallel to $\overline{ED}$. The angles $AEB$ and $ABE$ are in the ratio $4 : 5$.
What is the degree measure of angle $BCD$?

(A)$120$ (B)$125$ (C)$130$ (D)$135$ (E)$140$
AMC 10B, 2011, Problem 18
Rectangle $ABCD$ has $AB = 6$ and $BC = 3$. Point $M$ is chosen on side $AB$ so that $\angle AMD = \angle CMD$. What is the degree measure of $\angle AMD$?
(A)$15$ (B)$30$ (C)$45$ (D)$60$ (E)$75$
AMC 10B, 2011, Problem 20
Rhombus $ABCD$ has side length $2$ and $\angle B = 120^{\circ}$. Region $R$ consists of all points inside the rhombus that are closer to vertex $B$ than any of the other three vertices. What is the area of $R$?
(A)$\frac{\sqrt{3}}{3}$ (B)$\frac{\sqrt{3}}{2}$ (C)$\frac{2\sqrt{3}}{3}$ (D)$1 + \frac{\sqrt{3}}{3}$ (E)$2$
AMC 10B, 2011, Problem 22
A pyramid has a square base with sides of length $1$ and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?
(A)$5\sqrt{2} - 7$ (B) $7 - 4\sqrt{3}$ (C) $\frac{2\sqrt{2}}{27}$(D) $\frac{\sqrt{2}}{9}$ (E) $\frac{\sqrt{3}}{9}$
AMC 10B, 2011, Problem 24
A lattice point in an $xy$-coordinate system is any point $(x, y)$ where both $x$ and $y$ are integers. The graph of $y = mx +2$ passes through no lattice point with $0 < x \leq 100$ for all $m$ such that $1/2 < m < a$. What is the maximum possible value of $a$?
(A)$\frac{51}{101}$ (B)$\frac{50}{99}$ (C)$\frac{51}{100}$ (D)$\frac{52}{101}$ (E)$\frac{13}{25}$
AMC 10B, 2011, Problem 25
Let $T_1$ be a triangle with sides $2011, 2012,$ and $2013$. For $n \geq 1$, if $T_n = \triangle ABC$ and $D, E,$ and $F$ are the points of tangency of the incircle of $\triangle ABC$ to the sides $AB, BC$ and $AC,$ respectively, then $T_{n+1}$ is a triangle with side lengths $AD, BE,$ and $CF,$ if it exists. What is the perimeter of the last triangle in the sequence $( T_n )$?
(A)$\frac{1509}{8}$ (B)$\frac{1509}{32}$ (C)$\frac{1509}{64}$ (D)$\frac{1509}{128}$ (E)$\frac{1509}{256}$
AMC 10A, 2010, Problem 2
Four identical squares and one rectangle are placed together to form one large square as shown. The length of the rectangle is how many times as large as its width?

(A)$\frac{5}{4}$ (B)$\frac{4}{3}$ (C)$\frac{3}{2}$ (D)$2$ (E)$3$
AMC 10A, 2010, Problem 5
The area of a circle whose circumference is $24\pi$ is $k\pi$. What is the value of $k$?
(A)$6$ (B)$12$ (C)$24$ (D)$36$ (E)$144$
AMC 10A, 2010, Problem 7
Crystal has a running course marked out for her daily run. She starts this run by heading due north for one mile. She then runs northeast for one mile, then southeast for one mile. The last portion of her run takes her on a straight line back to where she started. How far, in miles, is this last portion of her run?
(A)$1 $ (B)$\sqrt{2}$ (C)$\sqrt{3}$ (D)$2$ (E)$2\sqrt{2}$
AMC 10A, 2010, Problem 12
Logan is constructing a scaled model of his town. The city's water tower stands 40 meters high,and the top portion is a sphere that holds 100,0 liters of water. Logan's miniature water tower holds 0.1 liters. How tall, in meters, should Logan make his tower?
(A)$0.04$ (B)$\frac{0.4}{\pi}$ (C)$0.4$ (D)$\frac{4}{\pi}$ (E)$4$
AMC 10A, 2010, Problem 14
Triangle $ABC$ has $AB=2 \cdot AC$. Let $D$ and $E$ be on $\overline{AB}$ and $\overline{BC}$, respectively, such that $\angle BAE = \angle ACD$. Let $F$ be the intersection of segments $AE$ and $CD$, and suppose that $\triangle CFE$ is equilateral. What is $\angle ACB$?
(A)$60^{\circ}$ (B)$75^{\circ}$ (C)$90^{\circ}$ (D)$105^{\circ}$ (E)$120^{\circ}$
AMC 10A, 2010, Problem 16
Nondegenerate $\triangle ABC$ has integer side lengths, $\overline{BD}$ is an angle bisector, $AD = 3$, and $DC=8$. What is the smallest possible value of the perimeter?
(A)$30$ (B)$33$ (C)$35$ (D)$36$ (E)$37$
AMC 10A, 2010, Problem 17
A solid cube has side length $3$ inches. A $2$-inch by $2$-inch square hole is cut into the center of each face. The edges of each cut are parallel to the edges of the cube, and each hole goes all the way through the cube. What is the volume, in cubic inches, of the remaining solid?
(A)7 (B) 8 (C) 10 (D)12 (E)15
AMC 10A, 2010, Problem 19
Equiangular hexagon $ABCDEF$ has side lengths $AB=CD=EF=1$ and $BC=DE=FA=r$. The area of $\triangle ACE$ is $70%$ of the area of the hexagon. What is the sum of all possible values of $r$?
(A)$\frac{4\sqrt{3}}{3}$ (B)$\frac{10}{3}$ (C)$4$ (D)$\frac{17}{4}$ (E)$6$
AMC 10A, 2010, Problem 20
A fly trapped inside a cubical box with side length $1$ meter decides to relieve its boredom by visiting each corner of the box. It will begin and end in the same corner and visit each of the other corners exactly once. To get from a corner to any other corner, it will either fly or crawl in a straight line. What is the maximum possible length, in meters, of its path?
(A)$4+4\sqrt{2}$ (B)$2+4\sqrt{2}+2\sqrt{3} $ (C)$2+3\sqrt{2}+3\sqrt{3}$
(D)$4\sqrt{2}+4\sqrt{3}$ (E)$3\sqrt{2}+5\sqrt{3}$
AMC 10A, 2010, Problem 22
Eight points are chosen on a circle, and chords are drawn connecting every pair of points. No three chords intersect in a single point inside the circle. How many triangles with all three vertices in the interior of the circle are created?
(A)$28$ (B)$56$ (C)$70$ (D)$84$ (E)$140$
AMC 10B, 2010, Problem 6
A circle is centered at $O$, $\overline{AB}$ is a diameter and $C$ is a point on the circle with $\angle COB = 50^{\circ}$. What is the degree measure of $\angle CAB$?
(A)$ 20$ (B)$25$ (C)$45$ (D)$50$ (E)$65$
AMC 10B, 2010, Problem 7
A triangle has side lengths $10$, $10$, and $12$. A rectangle has width $4$ and area equal to the area of the triangle. What is the perimeter of this rectangle?
(A)$ 16$ (B)$ 24$ (C)$28$ (D)$32$ (E)$36$
AMC 10B, 2010, Problem 16
A square of side length $1$ and a circle of radius $\frac{\sqrt{3}}{3}$ share the same center. What is the area inside the circle, but outside the square?
(A)$\frac{\pi}{3}-1$ (B)$\frac{2\pi}{9}-\frac{\sqrt{3}}{3}$ (C)$\frac{\pi}{18}$(D)$\frac{1}{4}$ (E) $\frac{2\pi}{9}$
AMC 10B, 2010, Problem 19
A circle with center $O$ has area $156\pi$. Triangle $ABC$ is equilateral, $\overline{BC}$ is a chord on the circle, $OA = 4\sqrt{3}$, and point $O$ is outside $\triangle ABC$. What is the side length of $\triangle ABC$?
(A)$2\sqrt{3}$ (B)$6$ (C)$4\sqrt{3}$ (D)$12$ (E)$18$
AMC 10B, 2010, Problem 20
Two circles lie outside regular hexagon $ABCDEF$. The first is tangent to $\overline{AB}$, and the second is tangent to $\overline{DE}$. Both are tangent to lines $BC$ and $FA$. What is the ratio of the area of the second circle to that of the first circle?
(A)$18$ (B)$27$ (C)$36$ (D)$81$ (E)$ 108$
AMC 10A, 2009, Problem 6
A circle of radius $2$ is inscribed in a semicircle, as shown. The area inside the semicircle but outside the circle is shaded. What fraction of the semicircle's area is shaded?
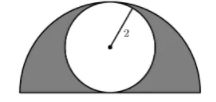
(A)$\frac{1}{2}$(B)$\frac{\pi}{6}$(C)$\frac{2}{\pi}$(D)$\frac{2}{3}$ (E)$\frac{3}{\pi}$
AMC 10A,2009,Problem 10
Triangle $ABC$ has a right angle at $B$. Point $D$ is the foot of the altitude from $B$,$AD=3$,and $DC=4$. What is the area of $\triangle ABC$?
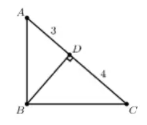
(A)$4\sqrt3$ (B)$7\sqrt3$ (C)$21$ (D)$14\sqrt3$ (E)$42$
AMC 10A,2009,Problem 11
One dimension of a cube is increased by $1$,another is decreased by $1$,and the third is left unchanged. The volume of the new rectangular solid is $5$ less than that of the cube. What was the volume of the cube?
(A)8 (B)27(C)64 (D)125 (E) 216
AMC 10A,2009,Problem 12
In quadrilateral $ABCD$,$AB=5$,$BC=17$,$CD=5$,$DA=9$,and $BD$ is an integer. What is $BD$?
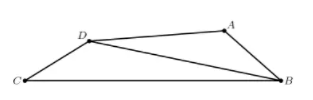
(A)11 (B) 12 (C) 13 (D) 14(E) 15
AMC 10A,2009,Problem 14
Four congruent rectangles are placed as shown. The area of the outer square is $4$ times that of the inner square. What is the ratio of the length of the longer side of each rectangle to the length of its shorter side?

(A)$3$ (B)$\sqrt{10}$ (C)$2+\sqrt{2}$ (D)$2\sqrt3$ (E)$4$
AMC 10A,2009,Problem 17
Rectangle $ABCD$ has $AB=4$ and $BC=3$. Segment $EF$ is constructed through $B$ so that $EF$ is perpendicular to $DB$,and $A$ and $C$ lie on $DE$ and $DF$,respectively. What is $EF$?
(A)$ 9$ (B)$10$ (C)$\frac{125}{12}$ (D)$\frac{103}{9}$ (E)$ 12$
AMC 10A,2009,Problem 19
Circle $A$ has radius $100$. Circle $B$ has an integer radius $r<100$ and remains internally tangent to circle $A$ as it rolls once around the circumference of circle $A$. The two circles have the same points of tangency at the beginning and end of circle $B$'s trip. How many possible values can $r$ have?
(A) 4 (B)8 (C) 9 (D) 50(E)90
AMC 10A, 2009, Problem 21
Many Gothic cathedrals have windows with portions containing a ring of congruent circles that are circumscribed by a larger circle. In the figure shown, the number of smaller circles is four. What is the ratio of the sum of the areas of the four smaller circles to the area of the larger circle?
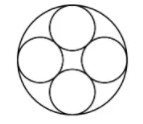
(A)$3-2\sqrt{2}$ (B)$2-\sqrt{2}$ (C)$4(3-2\sqrt{2}) $ (D)$\frac{1}{2}(3-\sqrt{2})$ (E)$2\sqrt{2}-2$
AMC 10A, 2009, Problem 23
Convex quadrilateral $ABCD$ has $AB=9$ and $CD=12$. Diagonals $AC$ and $BD$ intersect at $E$, $AC=14$, and $\triangle AED$ and $\triangle BEC$ have equal areas. What is $AE$?
(A)$\frac{9}{2}$ (B)$\frac{50}{11}$ (C)$\frac{21}{4}$ (D)$\frac{17}{3}$ (E)$6$
AMC 10B, 2009, Problem 4
A rectangular yard contains two flower beds in the shape of congruent isosceles right triangles. The remainder of the yard has a trapezoidal shape, as shown. The parallel sides of the trapezoid have lengths $15$ and $25$ meters. What fraction of the yard is occupied by the flower beds?

(A) $\frac {1}{8}$ (B)$\frac {1}{6}$ (C)$\frac {1}{5}$ (D) $\frac {1}{4}$ (E) $\frac {1}{3}$
AMC 10B, 2009, Problem 9
Segment $BD$ and $AE$ intersect at $C$, as shown, $AB=BC=CD=CE$, and $\angle A = \frac {5}{2} \angle B$. What is the degree measure of $\angle D$?

(A)$52.5$ (B)$55$ (C) $57.5$ (D)$60$ (E)$62.5$
AMC 10B, 2009, Problem 12
Distinct points $A$, $B$, $C$, and $D$ lie on a line, with $AB=BC=CD=1$. Points $E$ and $F$ lie on a second line, parallel to the first, with $EF=1$. A triangle with positive area has three of the six points as its vertices. How many possible values are there for the area of the triangle?
(A) 3 (B)4 (C) 5 (D) 6 (E) 7
AMC 10B, 2009, Problem 13
As shown below, convex pentagon $ABCDE$ has sides $AB=3$, $BC=4$, $CD=6$, $DE=3$, and $EA=7$. The pentagon is originally positioned in the plane with vertex $A$ at the origin and vertex $B$ on the positive $x$-axis. The pentagon is then rolled clockwise to the right along the $x$-axis. Which side will touch the point $x=2009$ on the $x$-axis?

(A)$\overline{AB}$ (B) $\overline{BC}$ (C)$\overline{CD}$ (D)$\overline{DE}$ (E)$\overline{EA}$
AMC 10B, 2009, Problem 16
Points $A$ and $C$ lie on a circle centered at $O$, each of $\overline{BA}$ and $\overline{BC}$ are tangent to the circle, and $\triangle ABC$ is equilateral. The circle intersects $\overline{BO}$ at $D$. What is $\frac{BD}{BO}$?
(A) $\frac {\sqrt2}{3}$ (B) $\frac {1}{2}$ (C) $\frac {\sqrt3}{3}$ (D)$\frac {\sqrt2}{2}$ (E)$\frac {\sqrt3}{2}$
AMC 10B, 2009, Problem 17
Five unit squares are arranged in the coordinate plane as shown, with the lower left corner at the origin. The slanted line, extending from $(c,0)$ to $(3,3)$, divides the entire region into two regions of equal area. What is $c$?
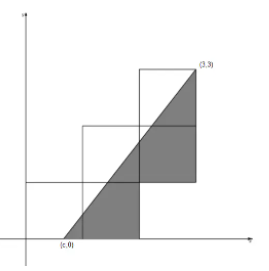
(A) $\frac {1}{2}$ (B)$\frac {3}{5}$ (C)$\frac {2}{3}$ (D) $\frac {3}{4}$ (E)$\frac {4}{5}$
AMC 10B, 2009, Problem 18
Rectangle $ABCD$ has $AB=8$ and $BC=6$. Point $M$ is the midpoint of diagonal $\overline{AC}$, and $E$ is on $AB$ with $\overline{ME}\perp\overline{AC}$. What is the area of $\triangle AME$?
(A)$\frac{65}{8}$ (B)$\frac{25}{3}$ (C) $9$ (D)$\frac{75}{8}$ (E)$\frac{85}{8}$
AMC 10B, 2009, Problem 20
Triangle $ABC$ has a right angle at $B$, $AB=1$, and $BC=2$. The angle bisector of $\angle A$ intersects side $\overline{BC}$ at $D$. What is $BD$?
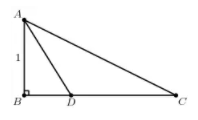
(A) $\frac {\sqrt{3} - 1}{2}$(B) $\frac {\sqrt5 - 1}{2}$ (C) $\frac {\sqrt5 + 1}{2}$ (D)$\frac {\sqrt6 + \sqrt2}{2}$ (E) $2\sqrt 3 - 1$
AMC 10B, 2009, Problem 22
A cubical cake with edge length $2$ inches is iced on the sides and the top. It is cut vertically into three pieces as shown in this top view, where $M$ is the midpoint of a top edge. The piece whose top is triangle $B$ contains $c$ cubic inches of cake and $s$ square inches of icing. What is $c+s$?

(A) $\frac{24}{5}$ B)$\frac{32}{5}$ (C) $8+\sqrt5$ (D) $5+\frac{16\sqrt5}{5}$ (E) $ 10+5\sqrt5$
AMC 10B, 2009, Problem 24
The keystone arch is an ancient architectural feature. It is composed of congruent isosceles trapezoids fitted together along the non-parallel sides, as shown. The bottom sides of the two end trapezoids are horizontal. In an arch made with $9$ trapezoids, let $x$ be the angle measure in degrees of the larger interior angle of the trapezoid. What is $x$?

(A) 100 (B) 102 (C) 104 (D) 106 (E) 108
AMC 10B, 2009, Problem 25
Each face of a cube is given a single narrow stripe painted from the center of one edge to the center of the opposite edge. The choice of the edge pairing is made at random and independently for each face. What is the probability that there is a continuous stripe encircling the cube?
(A)$\frac {1}{8}$ (B)$\frac {3}{16}$ (C)$\frac {1}{4}$ (D)$\frac {3}{8}$ (E)$\frac {1}{2}$
AMC 10A, 2008, Problem 2
A square is drawn inside a rectangle. The ratio of the width of the rectangle to a side of the square is $2:1$. The ratio of the rectangle's length to its width is $2:1$. What percent of the rectangle's area is in the square?
(A) 12.5 (B) 25 (C) 50(D) 75(E)87.5
AMC 10A, 2008, Problem 10
Each of the sides of a square $S_1$ with area $16$ is bisected, and a smaller square $S_2$ is constructed using the bisection points as vertices. The same process is carried out on $S_2$ to construct an even smaller square $S_3$. What is the area of $S_3$?
(A)$\frac{1}{2}$ (B)$1$ (C)$2$ (D)$3$ (E)$4$
AMC 10A, 2008, Problem 16
Points $A$ and $B$ lie on a circle centered at $O$, and $\angle AOB = 60^{\circ}$. A second circle is internally tangent to the first and tangent to both $\overline{OA}$ and $\overline{OB}$. What is the ratio of the area of the smaller circle to that of the larger circle?
(A)$\frac{1}{16}$ (B)$\frac{1}{9}$ (C)$\frac{1}{8}$ (D)$\frac{1}{6}$ (E)$\frac{1}{4}$
AMC 10A, 2008, Problem 17
An equilateral triangle has side length 6. What is the area of the region containing all points that are outside the triangle but not more than 3 units from a point of the triangle?
(A)$36+24\sqrt{3}$ (B)$54+9\pi$ (C)$54+18\sqrt{3}+6\pi$ (D)$(2\sqrt{3}+3)^2\pi$ (E)$9(\sqrt{3}+1)^2\pi$
AMC 10A, 2008, Problem 18
A right triangle has perimeter 32 and area 20. What is the length of its hypotenuse?
(A)$\frac{57}{4}$ (B)$\frac{59}{4}$ (C)$\frac{61}{4}$ (D)$\frac{63}{4}$ (E)$\frac{65}{4}$
AMC 10A, 2008, Problem 19
Rectangle $PQRS$ lies in a plane with $PQ=RS=2$ and $QR=SP=6$. The rectangle is rotated $90^{\circ}$ clockwise about $R$, then rotated $90^{\circ}$ clockwise about the point $S$ moved to after the first rotation. What is the length of the path traveled by point $P$?
(A)$(2\sqrt{3}+\sqrt{5})\pi$ (B)$6\pi$ (C)$(3+\sqrt{10})\pi$ (D)$(\sqrt{3}+2\sqrt{5})\pi$ (E)$ 2\sqrt{10}\pi$
AMC 10A, 2008, Problem 20
Trapezoid $ABCD$ has bases $\overline{AB}$ and $\overline{CD}$ and diagonals intersecting at $K$. Suppose that $AB = 9$, $DC = 12$, and the area of $\triangle AKD$ is $24$. What is the area of trapezoid $ABCD$?
(A)$92$ (B)$94$ (C)$96$ (D)$98$ (E)$100$
AMC 10A, 2008, Problem 21
A cube with side length $1$ is sliced by a plane that passes through two diagonally opposite vertices $A$ and $C$ and the midpoints $B$ and $D$ of two opposite edges not containing $A$ or $C$, as shown. What is the area of quadrilateral $ABCD$?

(A)$\frac{\sqrt{6}}{2}$ (B)$\frac{5}{4}$ (C)$\sqrt{2}$ (D) $\frac{5}{8}$ (E) $\frac{3}{4}$
AMC 10A, 2008, Problem 25
A round table has radius $4$. Six rectangular place mats are placed on the table. Each place mat has width $1$ and length $x$ as shown. They are positioned so that each mat has two corners on the edge of the table, these two corners being end points of the same side of length $x$. Further, the mats are positioned so that the inner corners each touch an inner corner of an adjacent mat. What is $x$?

(A)$2\sqrt{5}-\sqrt{3}$ (B)$3$ (C)$\frac{3\sqrt{7}-\sqrt{3}}{2}$ (D)$2\sqrt{3}$ (E)$ \frac{5+2\sqrt{3}}{2}$
AMC 10B, 2008, Problem 6
Points $B$ and $C$ lie on $AD$. The length of $AB$ is $4$ times the length of $BD$, and the length of $AC$ is $9$ times the length of $CD$. The length of $BC$ is what fraction of the length of $AD$?
(A)$1/36$ (B)$1/13$ (C)$ 1/10$ D)$ 5/36$ (E)$ 1/5$
AMC 10B, 2008, Problem 7
An equilateral triangle of side length $10$ is completely filled in by non-overlapping equilateral triangles of side length $1$. How many small triangles are required?
(A)$10$ (B)$25$ (C)$100$ (D)$250$ (E)$ 1000$
AMC 10B, 2008, Problem 10
Points $A$ and $B$ are on a circle of radius $5$ and $AB=6$. Point $C$ is the midpoint of the minor arc $AB$. What is the length of the line segment $AC$?
(A)$\sqrt{10}$ (B)$\frac{7}{2}$ (C)$\sqrt{14}$ (D)$\sqrt{15}$ (E)$4$
AMC 10B, 2008, Problem 14
Triangle $OAB$ has $O=(0,0)$, $B=(5,0)$, and $A$ in the first quadrant. In addition, $\angle ABO=90^{\circ}$ and $\angle AOB=30^{\circ}$. Suppose that $OA$ is rotated $90^{\circ}$ counterclockwise about $O$. What are the coordinates of the image of $A$?
(A)$( - \frac {10}{3}\sqrt {3},5) $ (B)$( - \frac {5}{3}\sqrt {3},5) $ (C)$(\sqrt {3},5)$ (D)$(\frac {5}{3}\sqrt {3},5) $ (E)$(\frac {10}{3}\sqrt {3},5)$
AMC 10B, 2008, Problem 15
How many right triangles have integer leg lengths $a$ and $b$ and a hypotenuse of length $b+1$, where $b<100$?
(A) 6(B) 7 (C) 8(D) 9(E) 10
AMC 10B, 2008, Problem 19
A cylindrical tank with radius $4$ feet and height $9$ feet is lying on its side. The tank is filled with water to a depth of $2$ feet. What is the volume of water, in cubic feet?
(A)$ 24\pi - 36 \sqrt {2} $ (B)$24\pi - 24 \sqrt {3} $ (C)$36\pi - 36 \sqrt {3}$ (D)$ 36\pi - 24 \sqrt {2}$ (E)$48\pi - 36 \sqrt {3}$
AMC 10B, 2008, Problem 20
The faces of a cubical die are marked with the numbers $1$, $2$, $2$, $3$, $3$, and $4$. The faces of another die are marked with the numbers $1$, $3$, $4$, $5$, $6$, and $8$. What is the probability that the sum of the top two numbers will be $5$, $7$, or $9$?
(A)$5/18$ (B)$7/18$ (C)$ 11/18$ (D)$3/4$ (E)$8/9$
AMC 10B, 2008, Problem 24
Quadrilateral $ABCD$ has $AB = BC = CD$, $\angle ABC = 70^{\circ}$ and $\angle BCD = 170^{\circ}$. What is the measure of angle $BAD$?
(A)75(B)80(C)85(D)90 (E)95
AMC 10A, 2007, Problem 8
Triangles $ABC$ and $ADC$ are isosceles with $AB=BC$ and $AD=DC$. Point $D$ is inside triangle $ABC$, angle $ABC$ measures 40 degrees, and angle $ADC$ measures 140 degrees. What is the degree measure of angle $BAD$?
(A)20(B)30(C)40(D)50(E)60
AMC 10A, 2007, Problem 14
A triangle with side lengths in the ratio $3 : 4 : 5$ is inscribed in a circle with radius $3$.
What is the area of the triangle?
(A)$8.64$
(B)$12$
(C)$5$
(D)$17.28$
(E)$18$
AMC 10A, 2007, Problem 15
Four circles of radius $1$ are each tangent to two sides of a square and externally tangent to a circle of radius $2$, as shown. What is the area of the square?

(A)$32$
(B)$22 + 12\sqrt {2}$
(C)$16 + 16\sqrt {3}$
(D)$48$
(E)$36 + 16\sqrt {2}$
AMC 10A, 2007, Problem 18
Consider the $12$-sided polygon $ABCDEFGHIJKL$, as shown. Each of its sides has length $4$,
and each two consecutive sides form a right angle.
Suppose that $\overline{AG}$ and $\overline{CH}$ meet at $M$.
What is the area of quadrilateral $ABCM$?

(A)$\frac {44}{3}$
(B)$16$
(C)$\frac {88}{5}$
(D)$20 $
(E)$\frac {62}{3}$
AMC 10A, 2007, Problem 19
A paint brush is swept along both diagonals of a square to produce the symmetric painted area, as shown. Half the area of the square is painted. What is the ratio of the side length of the square to the brush width?

(A)$2\sqrt {2} + 1$
(B)$3\sqrt {2}$
(C)$2\sqrt {2} + 2$
(D)$3\sqrt {2} + 1$
(E)$3\sqrt {2} + 2$
AMC 10A, 2007, Problem 24
Circles centered at $A$ and $B$ each have radius $2$, as shown. Point $O$ is the midpoint of $\overline{AB}$, and $OA = 2\sqrt {2}$. Segments $OC$ and $OD$ are tangent to the
circles centered at $A$ and $B$, respectively, and $EF$ is a common tangent.
What is the area of the shaded region $ECODF$?

(A)$\frac {8\sqrt {2}}{3}$
(B)$8\sqrt {2} - 4 - \pi $
(C)$4\sqrt {2} $
(D)$4\sqrt {2} + \frac {\pi}{8}$
(E)$8\sqrt {2} - 2 - \frac {\pi}{2}$
AMC 10B, 2007, Problem 4
The point $O$ is the center of the circle circumscribed about $\triangle ABC,$ with
$\angle BOC=120^{\circ}$ and $\angle AOB=140^{\circ}$.
What is the degree measure of $\angle ABC?$
(A)$35 $
(B)$40$
(C)$45$
(D)$50$
(E)$60$
AMC 10B, 2007, Problem 7
All sides of the convex pentagon $ABCDE$ are of equal length, and $\angle A= \angle B = 90^{\circ}.$ What is the degree measure of $\angle E?$
(A)$90$
(B)$108$
(C)$120$
(D)$144 $
(E)$150$
AMC 10B, 2007, Problem 10
wo points $B$ and $C$ are in a plane. Let $S$ be the set of all points $A$ in the plane for which $\triangle ABC$ has area $1.$ Which of the following describes $S?$
(A) two parallel lines
(B) a parabola
(C) a circle
(D) a line segment
(E) two points
AMC 10B, 2007, Problem 11
A circle passes through the three vertices of an isosceles triangle that has two sides of length $3$ and a base of length $2.$ What is the area of this circle?
(A)$2\pi $
(B)$\frac{5}{2}\pi$
(C) $\frac{81}{32}\pi$
(D)$3\pi$
(E)$\frac{7}{2}\pi$
AMC 10B, 2007, Problem 13
Two circles of radius $2$ are centered at $(2,0)$ and at $(0,2).$ What is the area of the intersection of the interiors of the two circles?
(A) $\pi -2$
(B)$\frac{\pi}{2}$
(C)$\frac{\pi \sqrt{3}}{3}$
(D)$2(\pi -2)$
(E)$\pi$
AMC 10B, 2007, Problem 15
The angles of quadrilateral $ABCD$ satisfy $\angle A=2 \angle B=3 \angle C=4 \angle D.$
What is the degree measure of $\angle A,$ rounded to the nearest whole number?
(A)$125$
(B)$144$
(C)$153$
(D)$173 $
(E) $180$
AMC 10B, 2007, Problem 17
Point $P$ is inside equilateral $\triangle ABC.$ Points $Q, R,$ and $S$ are the feet of the perpendiculars from $P$ to $\overline{AB}, \overline{BC},$ and $\overline{CA},$ respectively.
Given that $PQ=1, PR=2,$ and $PS=3,$ what is $AB?$
(A) $4 $
(B)$3\sqrt{3}$
(C)$6$
(D)$4\sqrt{3}$
(E)$9$
AMC 10B, 2007, Problem 18
A circle of radius $1$ is surrounded by $4$ circles of radius $r$ as shown. What is $r$?

(A)$\sqrt{2}$
(B)$1+\sqrt{2}$
(C)$\sqrt{6}$
(D)$3 $
(E) $2+\sqrt{2}$
AMC 10B, 2007, Problem 21
Right $\triangle ABC$ has $AB=3, BC=4,$ and $AC=5.$ Square $XYZW$ is inscribed in $\triangle ABC$ with $X$ and $Y$ on $\overline{AC}, W$ on $\overline{AB},$ and $Z$ on $\overline{BC}.$ What is the side length of the square?
(A)$\frac{3}{2}$
(B)$\frac{60}{37}$
(C) $\frac{12}{7}$
(D) $\frac{23}{13}$
(E) $2$
AMC 10B, 2007, Problem 23
A pyramid with a square base is cut by a plane that is parallel to its base and $2$ units from the base. The surface area of the smaller pyramid that is cut from the top is half the surface area of the original pyramid. What is the altitude of the original pyramid?
(A)$2$
(B)$2+\sqrt{2}$
(C)$1+2\sqrt{2}$
(D)$4$
(E)$4+2\sqrt{2}$
AMC 10A, 2006, Problem 7
The $8 \times 18$ rectangle $ABCD$ is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is $y$?

(A)$6$
(B)$7$
(C)$8$
(D)$9$
(E)$10$
AMC 10A, 2006, Problem 14
A number of linked rings, each $1$ cm thick, are hanging on a peg. The top ring has an outside diameter of $20$ cm. The outside diameter of each of the other rings is $1$ cm less than that of the ring above it.
The bottom ring has an outside diameter of $3$ cm. What is the distance, in cm, from the top of the top ring to the bottom of the bottom ring?

(A)$171$
(B)$173$
(C)$182$
(D)$188$
(E)$210$
AMC 10A, 2006, Problem 16
A circle of radius $1$ is tangent to a circle of radius $2$. The sides of $\triangle ABC$ are tangent to the circles as shown, and the sides $\overline{AB}$ and $\overline{AC}$ are congruent.
What is the area of $\triangle ABC$?

(A)$\frac{35}{2}$
(B)$15\sqrt{2}$
(C)$\frac{64}{3}$
(D)$16\sqrt{2}$
(E)$24$
AMC 10A, 2006, Problem 17
In rectangle $ADEH$, points $B$ and $C$ trisect $\overline{AD}$, and points $G$ and $F$ trisect $\overline{HE}$. In addition, $AH=AC=2$, and $AD = 3$.
What is the area of quadrilateral $WXYZ$ shown in the figure?
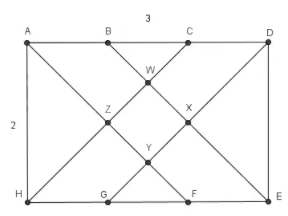
(A)$\frac{1}{2}$
(B)$\frac{\sqrt{2}}{2}$
(C)$\frac{\sqrt{3}}{2}$
(D)$\frac{2\sqrt{2}}{2}$
(E)$\frac{2\sqrt{3}}{3}$
AMC 10A, 2006, Problem 23
Circles with centers $A$ and $B$ have radii $3$ and $8$, respectively. A common internal tangent intersects the circles at $C$ and $D$, respectively.
Lines $AB$ and $CD$ intersect at $E$, and $AE=5$. What is $CD$?

(A)$13$
(B)$\frac{44}{3}$
(C)$\sqrt{221}$
(D)$\sqrt{255}$
(E)$\frac{55}{3}$
AMC 10A, 2006, Problem 24
Centers of adjacent faces of a unit cube are joined to form a regular octahedron.
What is the volume of this octahedron?
(A)$\frac{1}{8}$
(B)$\frac{1}{6}$
(C)$\frac{1}{4}$
(D)$\frac{1}{3}$
(E)$\frac{1}{2}$
AMC 10B, 2006, Problem 4
Circles of diameter $1$ inch and $3$ inches have the same center.
The smaller circle is painted red, and the portion outside the smaller circle and inside the larger circle is painted blue.
What is the ratio of the blue-painted area to the red-painted area?
(A) $2$
(B)$3$
(C) $6$
(D)$8$
(E) $9$
AMC 10B, 2006, Problem 6
A region is bounded by semicircular arcs constructed on the side of a square whose sides measure $\frac{2}{\pi}$, as shown. What is the perimeter of this region?

(A) $\frac{4}{\pi}$
(B)$2$
(C)$\frac{8}{\pi}$
(D) $4$
(E) $\frac{16}{\pi}$
AMC 10B, 2006, Problem 8
A square of area $40$ is inscribed in a semicircle as shown. What is the area of the semicircle?

(A) $20\pi$
(B) $25\pi$
(C)$30\pi$
(D) $40\pi$
(E) $50\pi$
AMC 10B, 2006, Problem 10
In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is $15$. What is the greatest possible perimeter of the triangle?
(A) $43$
(B) $44$
(C)$45$
(D) $46$
(E)$47$
AMC 10B, 2006, Problem 15
Rhombus $ABCD$ is similar to rhombus $BFDE$. The area of rhombus $ABCD$ is $24$ and
$\angle BAD = 60^{\circ}$. What is the area of rhombus $BFDE$?

(A) $6$
(B)$4\sqrt{3}$
(C)$8$
(D) $9$
(E) $6\sqrt{3}$
AMC 10B, 2006, Problem 19
A circle of radius $2$ is centered at $O$. Square $OABC$ has side length $1$. Sides $AB$ and $CB$ are extended past $B$ to meet the circle at $D$ and $E$, respectively.
What is the area of the shaded region in the figure, which is bounded by $BD$, $BE$, and the minor arc connecting $D$ and $E$?

(A) $\frac{\pi}{3}+1-\sqrt{3}$
(B) $\frac{\pi}{2}(2-\sqrt{3})$
(C)$\pi(2-\sqrt{3}) $
(D)$\frac{\pi}{6}+\frac{\sqrt{3}+1}{2}$
(E) $\frac{\pi}{3}-1+\sqrt{3}$
AMC 10B, 2006, Problem 20
In rectangle $ABCD$, we have $A=(6,-22)$, $B=(2006,178)$, $D=(8,y)$, for some integer $y$.
What is the area of rectangle $ABCD$?
(A) $4000$
(B) $4040$
(C) $4400$
(D)$40,000$
(E) $40,400$
AMC 10B, 2006, Problem 23
A triangle is partitioned into three triangles and a quadrilateral by drawing two lines from vertices to their opposite sides.
The areas of the three triangles are $3, 7,$ and $7$ as shown. What is the area of the shaded quadrilateral?

(A) $15$
(B) $17$
(C)$\frac{35}{2}$
(D)$18$
(E) $\frac{55}{3}$
AMC 10B, 2006, Problem 24
Circles with centers $O$ and $P$ have radii $2$ and $4$, respectively, and are externally tangent.
Points $A$ and $B$ on the circle with center $O$ and points $C$ and $D$ on the circle with center $P$ are such that $AD$ and $BC$ are common external tangents to the circles.
What is the area of the concave hexagon $AOBCPD$?

(A)$18\sqrt{3}$
(B)$24\sqrt{2}$
(C)$36$
(D)$24\sqrt{3}$
(E)$32\sqrt{2}$