Australian Mathematics Competition - 2020 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

How many pieces have been placed in the jigsaw puzzle so far?

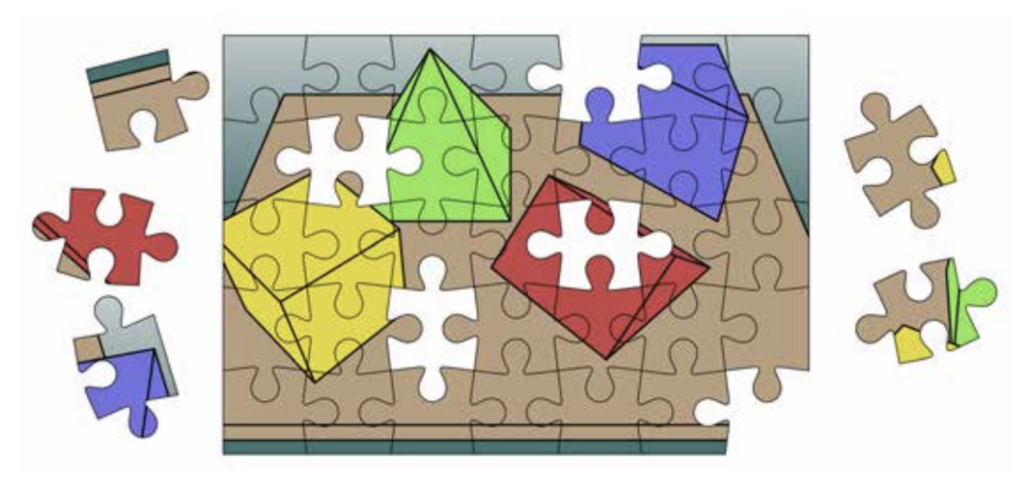
(A) 25 (B) 27 (C) 30 (D) 33 (E) 35

Problem 2:

What is half of 2020 ?

(A) 20 (B) 101 (C) 110 (D) 1001 (E) 1010

Problem 3:

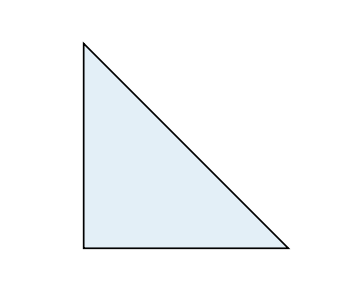
What is the perimeter of this triangle?

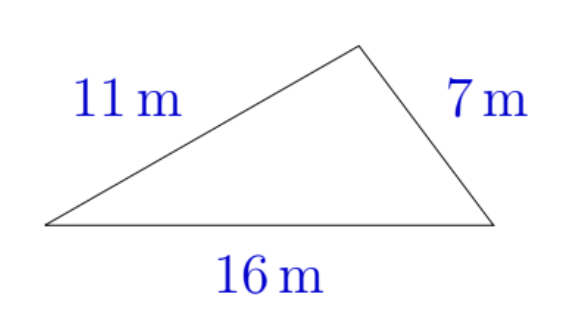
(A) 33 m (B) 34 m (C) 35 m (D) 36 m (E) 37 m

Problem 4:

Which fraction is the largest?

(A) one-half (B) one-quarter (C) one-third (D) three-quarters (E) six-tenths

Problem 5:

A protractor is used to measure angle (P X Q). The angle is

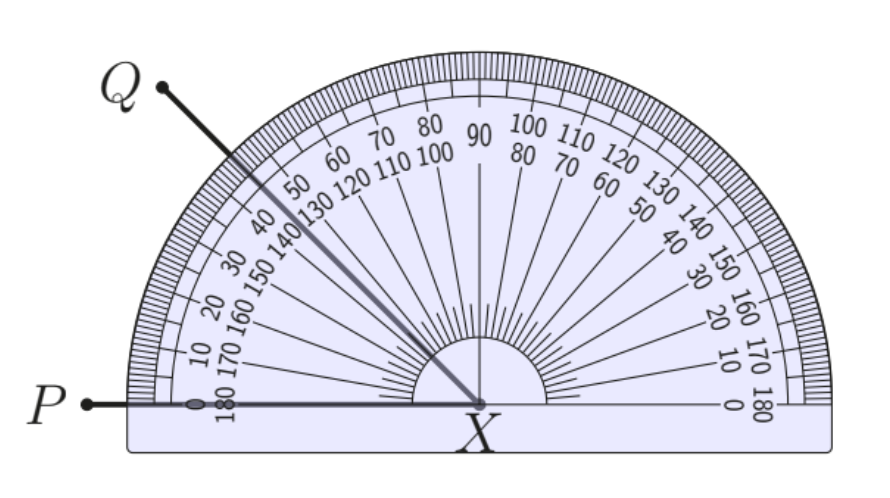
(A) $45^{\circ}$ (B) $55^{\circ}$ (C) $135^{\circ}$ (D) $145^{\circ}$ (E) $180^{\circ}$

Problem 6:

Some friends are walking to a lake in the mountains. First they climb a hill before they walk down to the lake. Which graph most accurately represents their journey?

Problem 7:

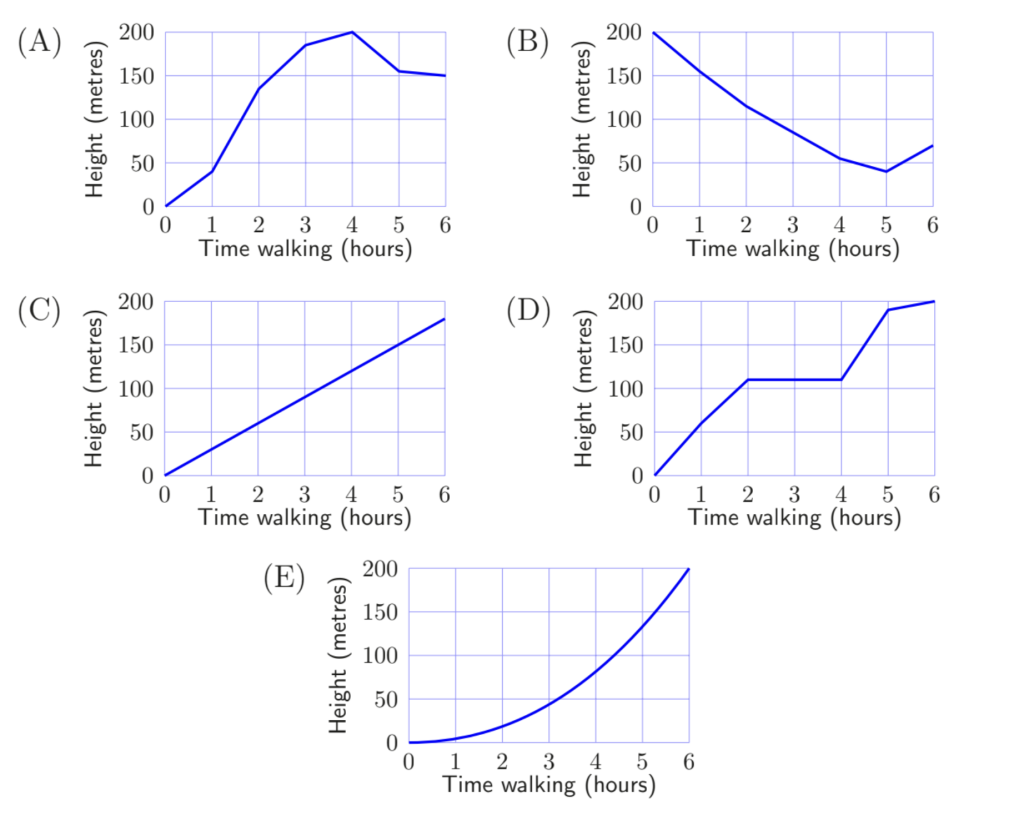
How many tenths are in 6.2 ?

(A) 62 (B) 8 (C) 4 (D) 12 (E) 36

Problem 8:

The graph shows the number of eggs laid by backyard chickens Nony and Cera for the first six months of the year.

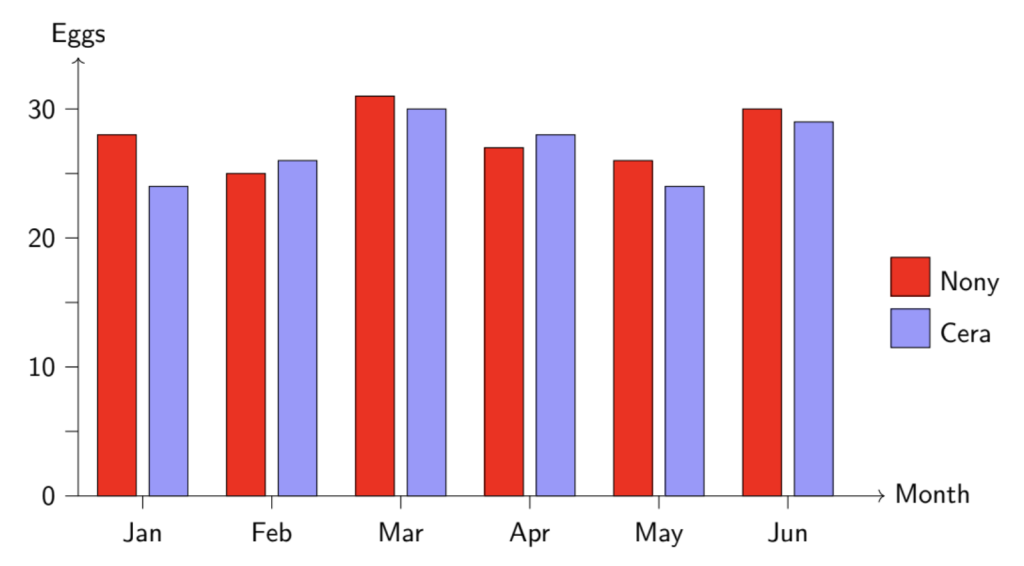
In how many months did Nony lay more eggs than Cera?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 9:

A class of 24 students, all of different heights, is standing in a line from tallest to shortest. Mary is the 8th tallest and John is the 6 th shortest. How many students are standing between them in the line?

(A) 6 (B) 7 (C) 8 (D) 9 (E) 10

Problem 10:

Maria divided a rectangle into a number of identical squares and coloured some of them in, as shown. She wants three-quarters of the rectangle's area to be coloured in altogether. How many more squares does she need to colour in?

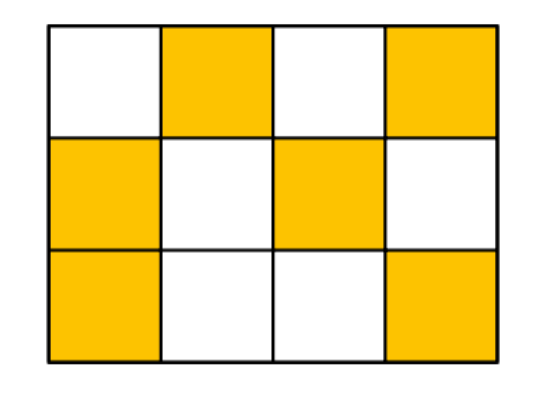
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4

Problem 11:

At the end of a game of marbles, Lei has 15 marbles, Dora has 8 and Omar has 4 . How many marbles must Lei give back to his friends if they want to start the next game with an equal number each?

(A) 5 (B) 6 (C) 7 (D) 8 (E) 9

Problem 12:

In the grid, the total of each row is given at the end of the row, and the total of each column is given at the bottom of the column.
The value of $N$ is

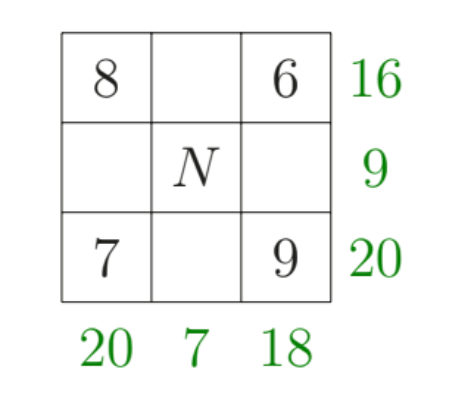
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 13:

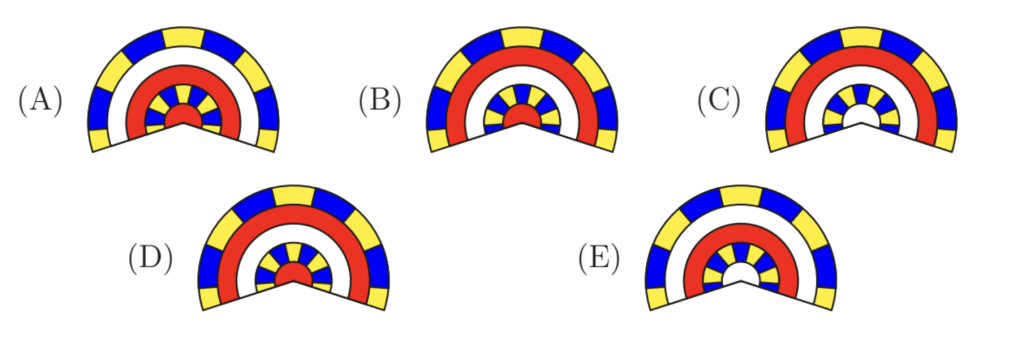
At his birthday party, Ricky and his friends wear stripy paper hats in the shape of a cone, as shown on the left. After the party, Ricky makes a straight cut in one of the hats all the way up to the point at the top, as shown on the right.

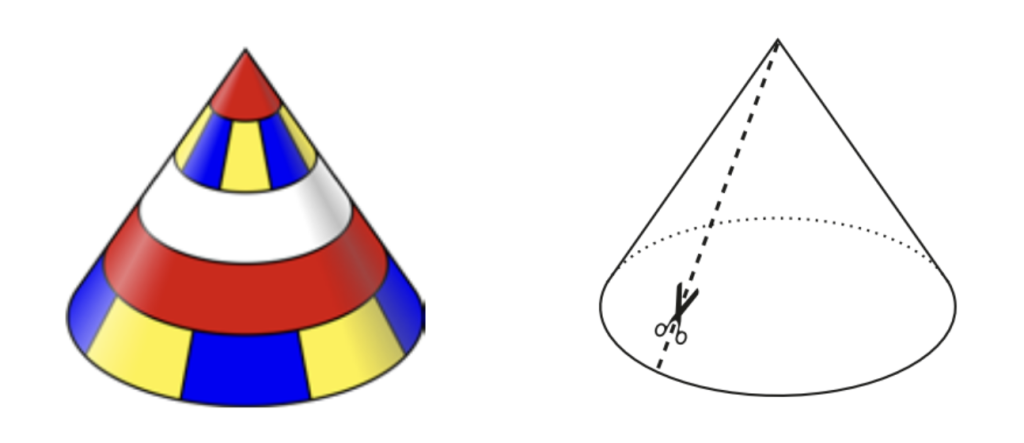
Which of the following best matches what the hat will look like when Ricky flattens it out on the table?

Problem 14:

Emma is going to write all the numbers from 1 to 50 in order. She writes 25 digits on the first line of her page. What was the last number she wrote on this line?

(A) 13 (B) 15 (C) 17 (D) 19 (E) 21

Problem 15:

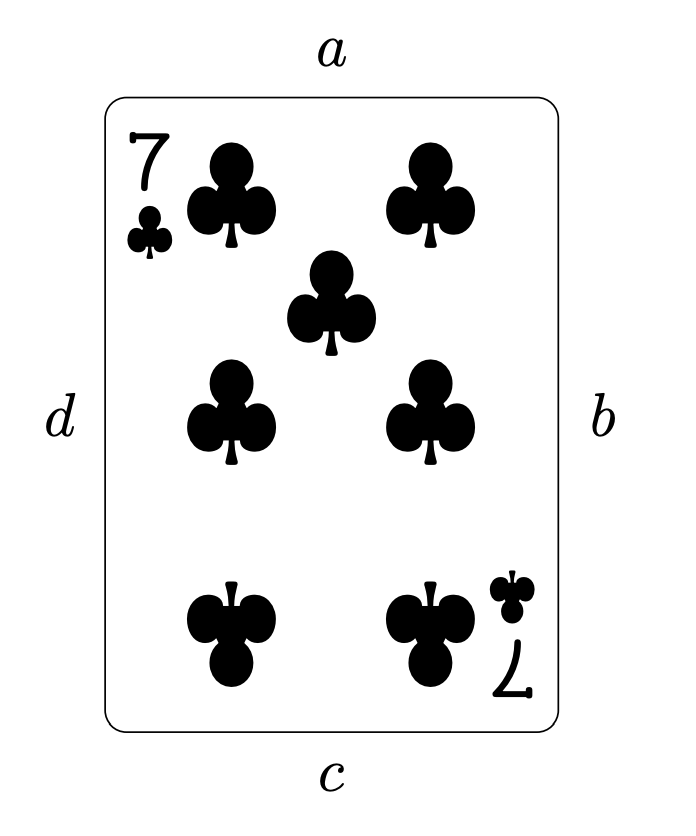
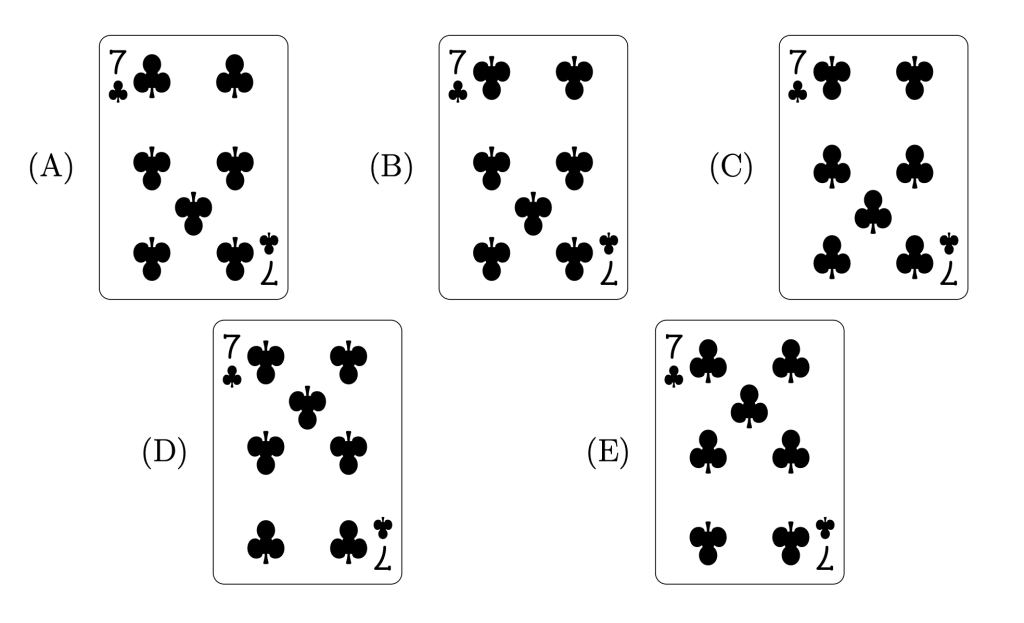
The playing card shown is flipped over along edge $b$ and then flipped over again along edge $c$. What does it look like now?

Problem 16:

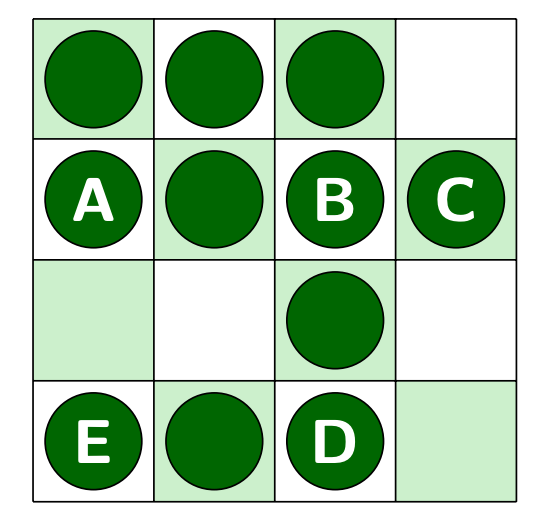
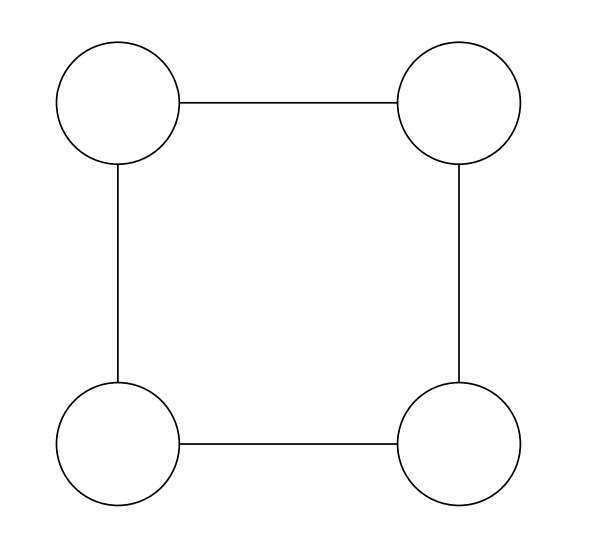
Which labelled counter should you remove so that no two rows have the same number of counters and no two columns have the same number of counters?

Problem 17:

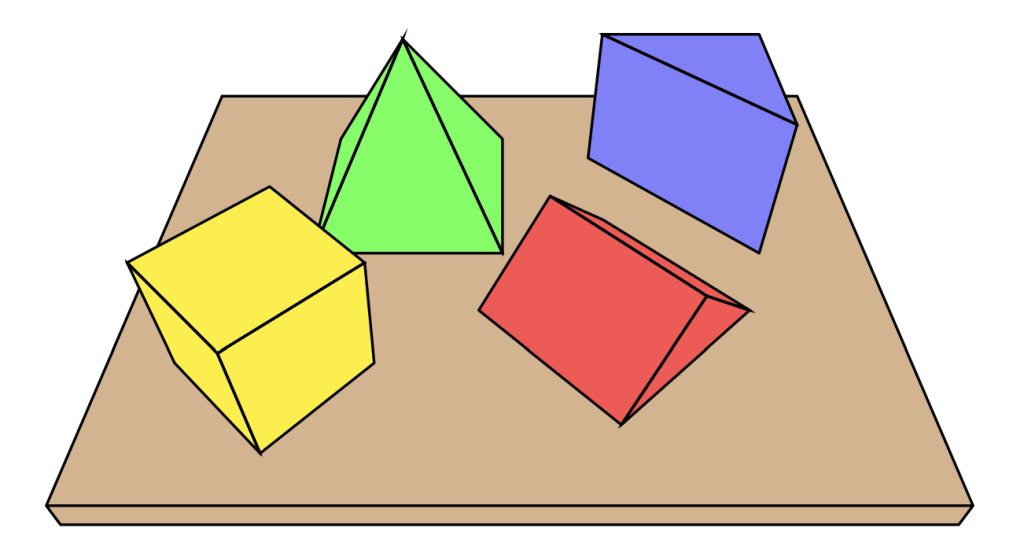
Aidan puts a range of 3D shapes on his desk at school. This is the view from his side of the desk:

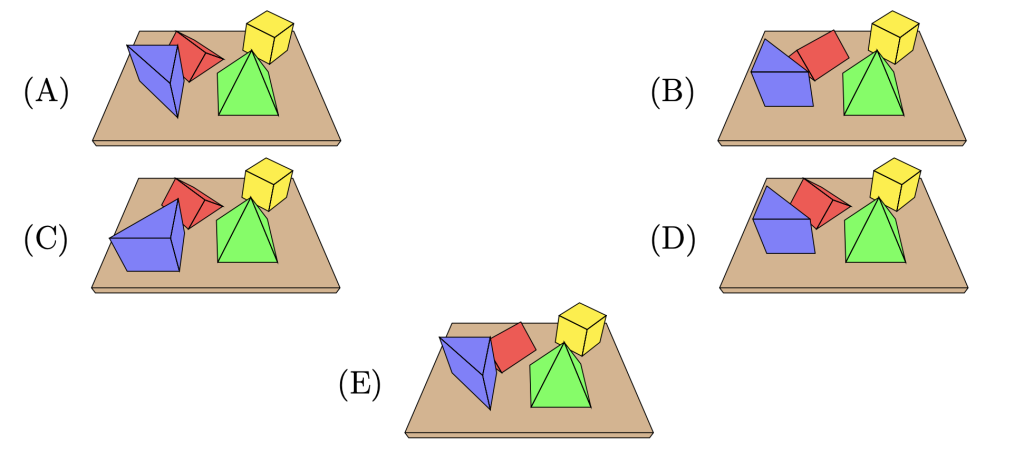
Nadia is sitting on the opposite side of the desk facing Aidan. Which of the following diagrams best represents the view from Nadia's side of the desk?

Problem 18:

The area of each of the five equilateral triangles in the diagram is 1 square metre. What is the shaded area?

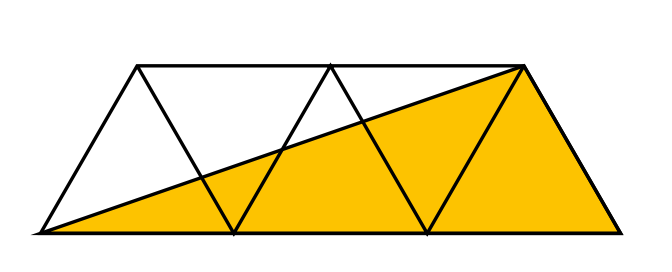
(A) $1.5 \mathrm{~m}^2$ (B) $2 \mathrm{~m}^2$ (C) $2.5 \mathrm{~m}^2$ (D) $3 \mathrm{~m}^2$ (E) $3.5 \mathrm{~m}^2$

Problem 19:

Kayla is 5 years old and Ryan is 13 years younger than Cody. One year ago, Cody's age was twice the sum of Kayla's and Ryan's age. Find the sum of the three children's current ages.

(A) 10 (B) 22 (C) 26 (D) 30 (E) 36

Problem 20:

Mary has a piece of paper. She folds it exactly in half. Then she folds it in half again. She finishes up with this shape.

Which of the shapes $P, Q$ and $R$ shown below could have been her starting shape?

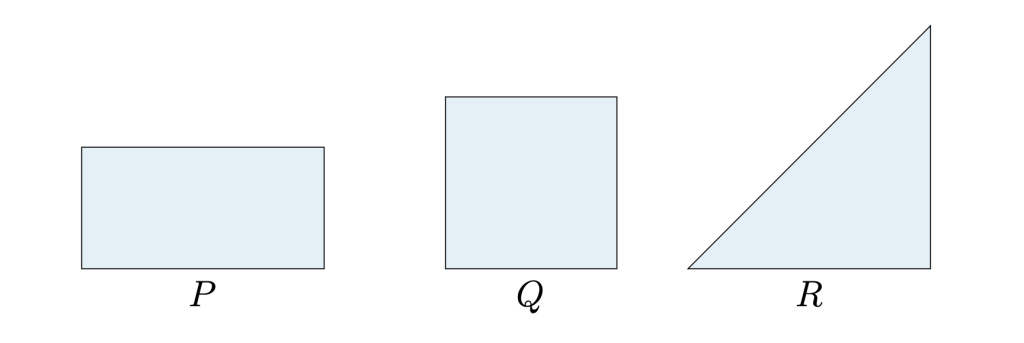
(A) only $P$ (B) only $Q$ (C) only $R$ (D) only $P$ and $R$ (E) all three

Problem 21:

Four positive whole numbers are placed at the vertices of a square. On each edge, the difference between the two numbers at the vertices is written. The four edge numbers are $1,2,3$ and 4 in some order. What is the smallest possible sum of the numbers at the vertices?

(A) 10 (B) 11 (C) 12 (D) 13 (E) 14

Problem 22:

The large rectangle shown has been divided into 4 smaller rectangles. The perimeters of three of these are $10 \mathrm{~cm}, 16 \mathrm{~cm}$ and 20 cm . The fourth rectangle does not have the largest or the smallest perimeter of the four smaller rectangles.

What, in centimetres, is the perimeter of the large rectangle?

(A) 26 (B) 30 (C) 32 (D) 36 (E) 46

Problem 23:

A bale of hay can be eaten by a horse in 2 days, by a cow in 3 days and by a sheep in 12 days. A farmer has 22 bales of hay and one horse, one cow and one sheep to feed. How many days will his bales last?

(A) 20 (B) 22 (C) 24 (D) 26 (E) 28

Problem 24:

This rectangle is 36 cm long. It is cut into two pieces and rearranged to form a square, as shown.

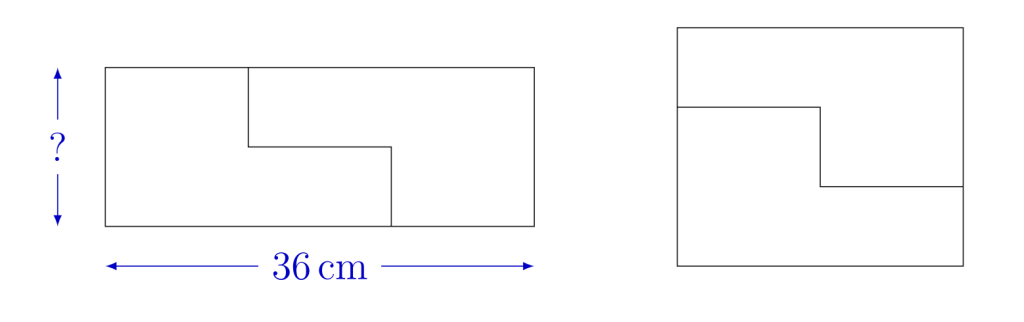
What is the height of the original rectangle?

(A) 14 cm (B) 16 cm (C) 18 cm (D) 20 cm (E) 24 cm

Problem 25:

A bottle with a sealed lid contains some water. The diagram shows this bottle up the right way and upside down. How full is the bottle?

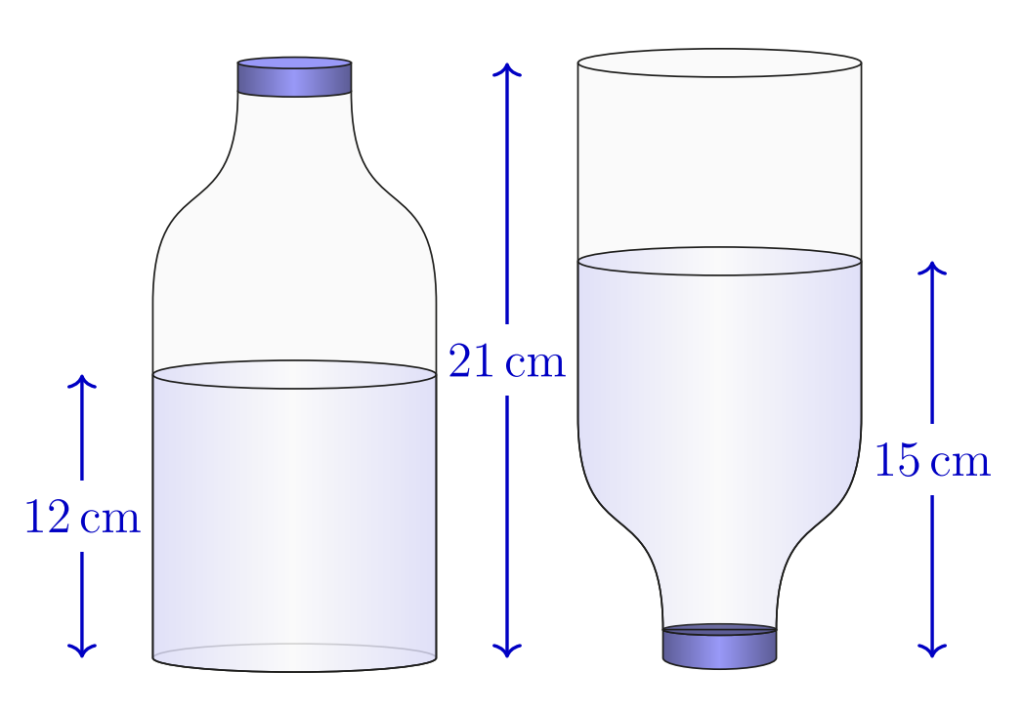
(A) $\frac{1}{2}$ (B) $\frac{4}{7}$ (C) $\frac{5}{7}$ (D) $\frac{2}{3}$ (E) $\frac{9}{14}$

Problem 26:

A number is oddtastic if all of its digits are odd. For example, 9,57 and 313 are oddtastic. However, 50 and 787 are not oddtastic, since 0 and 8 are even digits. How many of the numbers from 1 to 999 are oddtastic?

Problem 27:

On my chicken farm where I have 24 pens, the pens were a bit crowded. So I built 6 more pens, and the number of chickens in each pen reduced by 6 . How many chickens do I have?

Problem 28:

How many even three-digit numbers are there where the digits add up to $8 ?$

Problem 29:

Madeleine types her three-digit Personal Identification Number (PIN) into this keypad. All three digits are different, but the buttons for the first and second digits share an edge, and the buttons for the second and third digits share an edge. For instance, 563 is a possible PIN, but 536 is not, since 5 and 3 do not share an edge. How many possibilities are there for Madeleine's PIN?

Problem 30:

Writing one digit every second, you have half an hour to list as many of the counting numbers as you can, starting $1,2,3, \ldots$. At the end of half an hour, what number have you just finished writing?