Try this beautiful problem from the American Invitational Mathematics Examination I, AIME I, 1999 based on Squares and triangles.
The two squares share the same centre O and have sides of length 1, The length of AB is \(\frac{43}{99}\) and the area of octagon ABCDEFGH is \(\frac{m}{n}\) where m and n are relatively prime positive integers, find m+n.
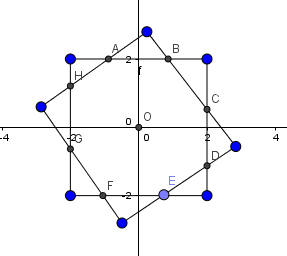
Squares
Triangles
Algebra
Answer: is 185.
AIME I, 1999, Question 4
Geometry Vol I to IV by Hall and Stevens
Triangle AOB, triangleBOC, triangleCOD, triangleDOE, triangleEOF, triangleFOG, triangleGOH, triangleHOA are congruent triangles
with each area =\(\frac{\frac{43}{99} \times \frac{1}{2}}{2}\)
then the area of all 8 of them is (8)\(\frac{\frac{43}{99} \times \frac{1}{2}}{2}\)=\(\frac{86}{99}\) then 86+99=185.
AMC - AIME Boot Camp... for brilliant students.
Use our exclusive one-on-one plus group class system to prepare for Math Olympiad
