Try this beautiful problem from Geometry based on the Area of the figure.
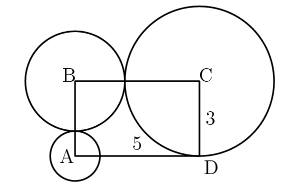
Rectangle $ABCD$ has sides $CD=3$ and $DA=5$. A circle of radius $1$ is centered at $A$, a circle of radius $2$ is centered at $B$, and a circle of radius $3$ is centered at $C$. Which of the following is closest to the area of the region inside the rectangle but outside all three circles?
Geometry
Rectangle
Circle
Answer: $4.0$
AMC-8 (2014) Problem 20
Pre College Mathematics
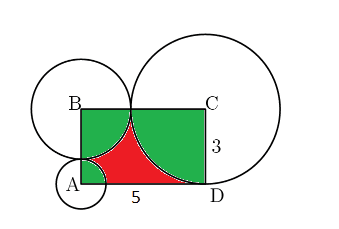
To Find out the area of the region inside the rectangle but outside all three circles,( i.e the red shaded region in the above figure), we have to find out the area of the Rectangle -the area of three quarter circle inside the circle(i.e green shaded region)
Can you now finish the problem ..........
To find out the area of the rectangle, AD=5 and CD=3 are given. to find out the area of the three-quarter circles, the radii are 1,2 & 3 respectively.
Now area of Rectangle=\(AD \times CD\) and area of quarter circles =\(\frac{\pi r^2}{4}\),where \(r\)=Radius of the circle
can you finish the problem........

Area of the rectangle=\( 5 \times 3\)=15 sq.unit
Area of the quarter circle with the center C=\(\frac{\pi (3)^2}{4}\)=\(\frac{9 \pi}{4}\) sq.unit
Area of the quarter circle with the center B= \(\frac{\pi (2)^2}{4}\) =\(\frac{4 \pi}{4}\)=\(\pi\) sq.unit
Area of the quarter circle with the center C= \(\frac{\pi (1)^2}{4}\) =\(\frac{\pi}{4}\) sq.unit
Therefore the area of the region inside the rectangle but outside all three circles,( i.e the red shaded region in the above figure) =(15- \(\frac{9 \pi}{4}\)- \(\pi\) - \(\frac{\pi}{4}\) )=15-\(\frac{7\pi}{2}\)=15-11=4 sq.unit (Taking \(\pi =\frac{22}{7}\))