Try this beautiful problem from the American Invitational Mathematics Examination I, AIME I, 2009 based on Triangles and sides.
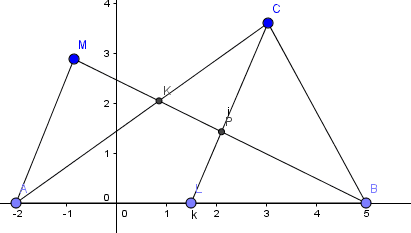
Triangle ABC AC=450 BC=300 points K and L are on AC and AB such that AK=CK and CL is angle bisectors of angle C. let P be the point of intersection of Bk and CL and let M be a point on line Bk for which K is the mid point of PM AM=180, find LP
Angles
Triangles
Side Length
Answer: is 72.
AIME I, 2009, Question 5
Geometry Vol I to IV by Hall and Stevens
since K is mid point of PM and AC quadrilateral AMCP is a parallelogram which implies AM parallel LP and triangle AMB is similar to triangle LPB
then \(\frac{AM}{LP}=\frac{AB}{LB}=\frac{AL+LB}{LB}=\frac{AL}{LB}+1\)
from angle bisector theorem, \(\frac{AL}{LB}=\frac{AC}{BC}=\frac{450}{300}=\frac{3}{2}\) then \(\frac{AM}{LP}=\frac{AL}{LB}+1=\frac{5}{2}\)
\(\frac{180}{LP}=\frac{5}{2}\) then LP=72.
AMC - AIME Boot Camp... for brilliant students.
Use our exclusive one-on-one plus group class system to prepare for Math Olympiad