Find the value of \(m\) such that \(2 x^2+3 x+m\) has a minimum value of \(9\) .
(A) \(\frac{9}{8}\)
(B) \(-\frac{9}{8}\)
(C) \(\frac{81}{8}\)
(D) \(-\frac{81}{8}\)
(E) \(\frac{63}{8}\)
Which of the following is true?
(A) \(\sin \left(105^{\circ}\right)-\cos \left(105^{\circ}\right)=\frac{\sqrt{3}}{2}\)
(B) \(\sin \left(105^{\circ}\right)-\cos \left(105^{\circ}\right)=\frac{\sqrt{3}}{\sqrt{2}}\)
(C) \(\sin \left(105^{\circ}\right)+\cos \left(105^{\circ}\right)=\frac{1}{2}\)
(D) \(\sin \left(105^{\circ}\right)+\cos \left(105^{\circ}\right)=\frac{1}{\sqrt{3}}\)
(E) None of the above.
If \(\log {\sqrt{2}} x=10-3 \log {\sqrt{2}} 10\), find \(x\).
(A) 0.32
(B) 0.032
(C) 0.0032
(D) 0.64
(E) 0.064
If \((x-5)^2+(y-5)^2=5^2\), find the smallest value of \((x+5)^2+(y+5)^2\).
(A) \(225-100 \sqrt{2}\)
(B) \(225+100 \sqrt{2}\)
(C) \(225 \sqrt{2}\)
(D) \(100 \sqrt{2}\)
(E) None of the above
Suppose \(\cos \left(180^{\circ}+x\right)=\frac{4}{5}\), where \(90^{\circ}<x<180^{\circ}\). Find \(\tan (2 x)\).
(A) \(\frac{24}{7}\)
(B) \(\frac{7}{24}\)
(C) \(-\frac{24}{7}\)
(D) \(-\frac{7}{24}\)
(E) \(-\frac{24}{25}\)
Suppose the roots of \(x^2+11 x+3=0\) are \(p\) and \(q\), and the roots of \(x^2+B x-C=0\) are \(p+1\) and \(q+1\). Find \(C\).
If the smallest possible value of \((A-x)(23-x)(A+x)(23+x)\) is \(-(48)^2\), find the value of \(A\) if \(A>0\).
Find the smallest positive odd integer greater than 1 that is a factor of
\((2023)^{2023}+(2026)^{2026}+(2029)^{2029}\) .
Find the remainder of \(7^{2023}+9^{2023}\) when divided by \(64\) .
Let \(x, y, z>1\), and let \(A\) be a positive number such that \(\log x A=30, \log _y A=50\) and \(\log {x y}(A z)=150\). Find
\(\left(\log _A z\right)^2\).
Find the largest integer that is less than
\(\text { - } \frac{3^{10}-2^{10}}{10 !}\left(\frac{1}{1 ! 9 ! 2}+\frac{1}{2 ! 8 ! 2^2}+\frac{1}{3 ! 7 ! 2^3}+\cdots+\frac{1}{9 ! 1 ! 2^9}\right)^{-1}\) .
Here, \(n !=n \cdot(n-1) \cdots 3 \cdot 2 \cdot 1\). For example, \(5 !=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120\).
Consider the following simultaneous equations:
\( x y^2+x y z=91\)
\( x y z-y^2 z=72\),
where \(x, y\), and \(z\) are positive integers. Find the maximum value of \(x z\).
Let \(x\) be a real number such that
\(\frac{\sin ^4 x+\cos ^4 x}{\sin ^2 x+\cos ^4 x}=\frac{8}{11}\) .
Assuming \(\sin ^2 x>\frac{1}{2}\), find the value of \(\sqrt{28}\left(\sin ^4 x-\cos ^4 x\right)\).
A sequence \(a_1, a_2, \ldots\), is defined by
\(a_1=5, a_2=7, a_{n+1}=\frac{a_n+1}{a_{n-1}} \text { for } n \geq 2\) .
Find the value of \(100 \times a_{2023}\)
Let \(C\) be a constant such that the equation \(5 \cos x+6 \sin x-C=0\) have two distint roots \(a\) and \(b\), where \(0<b<a<\pi\). Find the value of \(61 \times \sin (a+b)\).
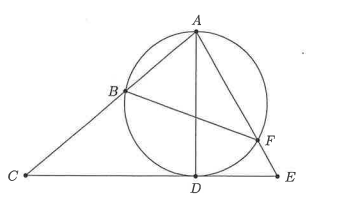
In the diagram below, \(C E\) is tangent to the circle at point \(D, A D\) is a diameter of the circle, and \(A B C, A F E\) are straight lines. It is given that \(\frac{A B}{A C}=\frac{16}{41}\) and \(\frac{A F}{A E}=\frac{49}{74}\). Let \(\tan (\angle C A E)=\frac{m}{n}\), where \(m, n\) are positive integers and \(\frac{m}{n}\) is a fraction in its lowest form. Find the sum \(m+n\).
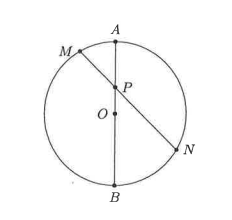
In the diagram below, \(A B\) is a diameter of the circle with centre \(O, M N\) is a chord of the circle that intersects \(A B\) at \(P, \angle B O N\) and \(\angle M O A\) are acute angles, \(\angle M P A=45^{\circ}\), \(M P=\sqrt{56}\), and \(N P=12\). Find the radius of the circle.
Let \(f(x)=\cos ^2\left(\frac{\pi x}{2}\right)\). Find the value of
\(f \left(\frac{1}{2023}\right)+f\left(\frac{2}{2023}\right)+\cdots+f\left(\frac{2021}{2023}\right)+f\left(\frac{2022}{2023}\right)\) .
Find the remainder when \(3^{2023}\) is divided by \(215\) .
Find the sum of the prime divisors of \(64000027\) .
Let \(\triangle A B C\) be an equilateral triangle. \(D, E, F\) are points on the sides such that
\(B D: D C=C E: E A=A F: F B=2: 1\) .
Suppose the area of the triangle bounded by \(A D, B E\) and \(C F\) is \(2023\) . Find the area of \(\triangle A B C\).

Find the number of possible ways of arranging \(m\) ones and \(n\) zeros in a row such that there are in total \(2 k+1\) strings of ones and zeros. For example, \(1110001001110001\) consists of 4 strings of ones and 3 strings of zeros.
Suppose that there exist numbers \(a, b, c\) and a function \(f\) such that for any real numbers \(x\) and \(y\),
\(f(x+y)+f(x-y)=2 f(x)+2 f(y)+a x+b y+c\) .
It is given that
\(f(2)=3, \quad f(3)=-5, \quad\)and \(\quad f(5)=7\) . Find the value of \(f(123)\).
Let \(f\) be a function such that for any nonzero number \(x\),
\(6 x f(x)+5 x^2 f(1 / x)+10=0\) .
Find the value of \(f(10)\).
Find the number of triangles such that all the sides are integers and the area equals the perimeter (in number).