Find x if \(\frac{79}{125}\left(\frac{79+x}{125+x}\right)=1.\)
(a) 0
(b) -46
(c) -200
(d) -204
Answer : D
The line \(2 x+a y=5\) passes through (-2,-1) and (1, b). What is the value of b ?
(a) \(-\frac{1}{2}\)
(b) \(-\frac{1}{3}\)
(c) \(-\frac{1}{4}\)
(d) \(-\frac{1}{6}\)
Answer : B
Let ABCD be a parallelogram. Two squares are constructed from its adjacent sides, as shown in the figure below. If \(\angle BAD=56^{\circ}\), find \(\angle ABE+\angle ADH+\angle FC G\), the sum of the three highlighted angles.

(a) \(348^{\circ}\)
(b) \(384^{\circ}\)
(c) \(416^{\circ}\)
(d) \(432^{\circ}\)
Answer : C
For how many integers x from 1 to 60 , inclusive, is the fraction \(\frac{x}{60}\) already in lowest terms?
(a) 15
(b) 16
(c) 17
(d) 18
Answer : B
Let r and s be the roots of the polynomial \(3 x^2-4 x+2\). Which of the following is a polynomial with roots \(\frac{r}{s}\) and \(\frac{s}{r}\) ?
(a) \(3 x^2+2 x+3\)
(b) \(3 x^2+2 x-3\)
(c) \(3 x^2-2 x+3\)
(d) \(3 x^2-2 x-3\)
Answer : C
If the difference between two numbers is a and the difference between their squares is b, where \(a, b>0\), what is the sum of their squares?
(a) \(\frac{a^2+b^2}{a}\)
(b) \(2\left(\frac{a+b}{a}\right)^2\)
(c) \(\left(a+\frac{b}{a}\right)^2\)
(d) \(\frac{a^4+b^2}{2 a^2}\)
Answer : D
Evaluate the sum
\([
\sum_{n=3}^{2017} \sin \left(\frac{(n !) \pi}{36}\right) .
]\)
(a) 0
(b) \(\frac{1}{2}\)
(c) \(-\frac{1}{2}\)
(d) 1
Answer : B
In \(\triangle ABC,D\) is the midpoint of BC. If the sides AB,BC, and CA have lengths 4,8 , and 6 , respectively, then what is the numerical value of \(AD^2 ?\)
(a) 8
(b) 10
(c) 12
(d) 13
Answer : B
Let A be a positive integer whose leftmost digit is 5 and let B be the number formed by reversing the digits of A. If A is divisible by 11,15,21, and 45 , then B is not always divisible by
(a) 11
(b) 15
(c) 21
(d) 45
Answer : C
In \(\triangle ABC\), the segments AD and AE trisect \(\angle BAC\). Moreover, it is also known that AB= 6, AD=3, AE=2.7, AC=3.8 and DE=1.8. The length of BC is closest to which of the following?
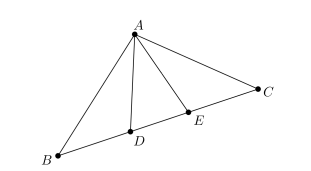
(a) 8
(b) 8.2
(c) 8.4
(d) 8.6
Answer : A
Let \({a_n} \) be a sequence of real numbers defined by the recursion \(a_{n+2}=a_{n+1}-a_n\) for all positive integers n. If \(a_{2013}=2015\), find the value of \(a_{2017}-a_{2019}+a_{2021}.\)
(a) 2015
(b) -2015
(c) 4030
(d) -4030
Answer : D
A lattice point is a point whose coordinates are integers. How many lattice points are strictly inside the triangle formed by the points (0,0),(0,7), and (8,0) ?
(a) 21
(b) 22
(c) 24
(d) 28
Answer : A
Find the sum of the solutions to the logarithmic equation
\([
x^{\log x}=10^{2-3 \log x+2(\log x)^2},
]\)
where \(\log x\) is the \(\log a\) rithm of x to the base 10 .
(a) 10
(b) 100
(c) 110
(d) 111
Answer : C
Triangle ABC has AB=10 and AC=14. A point P is randomly chosen in the interior or on the boundary of triangle ABC. What is probability that P is closer to AB than to AC ?
(a) 1 / 4
(b) 1 / 3
(c) 5 / 7
(d) 5 / 12
Answer : D
Suppose that \({a_n}\) is a nonconstant arithmetic sequence such that \(a_1=1\) and the terms \(a_3, a_{15}, a_{24}\) form a geometric sequence in that order. Find the smallest index n for which \(a_n<0.\)
(a) 50
(b) 51
(c) 52
(d) 53
Answer : C
Two red balls, two blue balls, and two green balls are lined up into a single row. How many ways can you arrange these balls such that no two adjacent balls are of the same color?
(a) 15
(b) 30
(c) 60
(d) 90
Answer : B
What is the sum of the last two digits of \(403^{\left(10^{10}+6\right)} ?\)
(a) 9
(b) 10
(c) 11
(d) 12
Answer : C
How many strictly increasing finite sequences (having one or more terms) of positive integers less than or equal to 2017 with an odd number of terms are there?
(a) \(2^{2016}\)
(b) \(\frac{4034 !}{(2017 !)^2}\)
(c) \(2^{2017}-2017^2\)
(d) \(2^{2018}-1\)
Answer : A
If one of the legs of a right triangle has length 17 and the lengths of the other two sides are integers, then what is the radius of the circle inscribed in that triangle?
(a) 8
(b) 14
(c) 11
(d) 10
Answer : A
Let N be the smallest three-digit positive number with exactly 8 positive even divisors. What is the sum of the digits of N ?
(a) 4
(b) 9
(c) 12
(d) 13
Answer : B
Let a, b, c be randomly chosen (in order, and with replacement) from the set \({1,2,3, \ldots, 999}\). If each choice is equally likely, what is the probability that \(a^2+b c\) is divisible by 3 ?
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{7}{27}\)
(d) \(\frac{8}{27}\)
Answer : A
Folding a rectangular sheet of paper with length \(\ell\) and width w in half along one of its diagonals, as shown in the figure below, reduces its "visible" area (the area of the pentagon below) by \(30 \%\). What is \(\frac{\ell}{w}\) ?
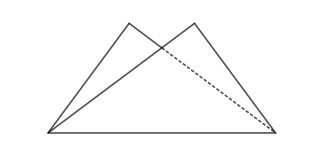
(a) \(\frac{4}{3}\)
(b) \(\frac{2}{\sqrt{3}}\)
(c) \(\sqrt{5}\)
(d) \(\frac{\sqrt{5}}{2}\)
Answer : C
Find the sum of all positive integers k such that k(k+15) is a perfect square.
(a) 63
(b) 65
(c) 67
(d) 69
Answer : C
Let \(f(n)=\frac{n}{3^r}\) where n is an integer, and r is the largest nonnegative integer such that n is divisible by \(3^r\). Find the number of distinct values of f(n) where \(1 \leq n \leq 2017\).
(a) 1344
(b) 1345
(c) 1346
(d) 1347
Answer : B
If A,B, and C are the angles of a triangle such that
\([
5 \sin A+12 \cos B=15
]\)
and
\([
12 \sin B+5 \cos A=2,
]\)
then the measure of angle C is
(a) \(150^{\circ}\)
(b) \(135^{\circ}\)
(c) \(45^{\circ}\)
(d) \(30^{\circ}\)
Answer : D
How many three-digit numbers are there such that the sum of two of its digits is the largest digit?
Answer : \(279(\text { or } 126)^1\)
In the figure, a quarter circle, a semicircle and a circle are mutually tangent inside a square of side length 2. Find the radius of the circle.
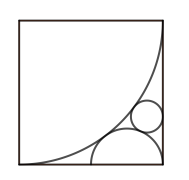
Answer : \(\frac{2}{9}\)
Find the minimum value of
\([
\frac{18}{a+b}+\frac{12}{a b}+8 a+5 b,
]\)
where a and b are positive real numbers.
Answer : 30
Suppose \(\frac{\tan x}{\tan y}=\frac{1}{3}\) and \(\frac{\sin 2 x}{\sin 2 y}=\frac{3}{4}\), where \(0<x, y<\frac{\pi}{2}\). What is the value of \(\frac{\tan 2 x}{\tan 2 y}\) ?
Answer : \(-\frac{3}{11}\)
Find the largest positive real number x such that
\([
\frac{2}{x}=\frac{1}{\lfloor x\rfloor}+\frac{1}{\lfloor 2 x\rfloor},
]\)
where \(\lfloor x\rfloor\) denotes the greatest integer less than or equal to x.
Answer : \(\frac{20}{7}\)