Problem 1
\(A B\) is a straight road of length 400 metres. From \(A\), Samrud runs at a speed of \(6 \mathrm{~m} / \mathrm{s}\) towards \(B\) and at the same time Saket starts from \(B\) and runs towards \(A\) at a speed of \(5 \mathrm{~m} / \mathrm{s}\). After reaching their destinations, they return with the same speeds. They repeat it again and again. How many times do they meet each other in 15 minutes?
A) 25
B) 23
C) 24
D) 20
Problem 2
In the adjoining figure, the measure of the angle \(x\) is
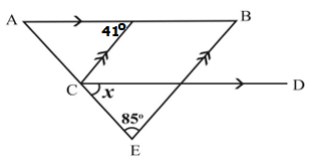
A) \(84^{\circ}\)
B) \(44^{\circ}\)
C) \(64^{\circ}\)
D) \(54^{\circ}\)
Problem 3
The value of \(x\) which satisfies \(\frac{1}{x+a}+\frac{1}{x+b}=\frac{1}{x+a+b}+\frac{1}{x}\) is
A) \(\frac{a+b}{2}\)
B) \(\frac{a-b}{2}\)
C) \(\frac{b-a}{2}\)
D) \(\frac{-(a+b)}{2}\)
Problem 4
Two sides of an isosceles triangle are 23 cm and 17 cm respectively. The perimeter of the triangle (in cm ) is
A) 63
В) 57
C) 63 or 57
D) 40
Problem 5
\(A B C D E\) is a pentagon with \(\angle B=90^{\circ}\) and \(\angle E=150^{\circ}\).
If \(\angle C+\angle D=180^{\circ}\) and \(\angle A+\angle D=180^{\circ}\), then the external angle \(\angle D\) is
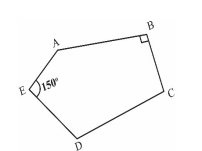
A) \(120^{\circ}\)
B) \(110^{\circ}\)
C) \(105^{\circ}\)
D) \(115^{\circ}\)
Problem 6
The unit's digit of the product \(3^{2025} \times 7^{2024}\) is
A) 1
B) 2
C) 3
D) 6
Problem 7
The smallest positive integer \(n\) for which \(18900 \times n\) is a perfect cube is
A) 1
B) 2
C) 3
D) 6
Problem 8
Two numbers \(a\) and \(b\) are respectively \(20 \%\) and \(50 \%\) more of a third number \(c\). The percentage of \(a\) to \(b\) is
A) 120 %
В) 80 %
C) 75 %
D) 110 %
Problem 9
If \(a+b=2, \frac{1}{a}+\frac{1}{b}=18\), then \(a^3+b^3\) lies between
A) 7 and 8
B) 6 and 7
C) 8 and 9
D) 5 and 6
Problem 10
If \(\sqrt{12+\sqrt[3]{x}}=\frac{7}{2}\) and \(x=\frac{p}{q^{\prime}}, p, \mathrm{q}\) are natural numbers with G.C.D. \((p, q)=1\), then \(p+q\) is
A) 65
В) 56
C) 45
D) 54
Problem 11
The smallest number of 4-digits leaving a remainder 1 when divided by 2 or
A) 5 as its unit digit
B) Only one zero as one of the digits
C) Exactly two zeroes as its digits
D) 7 as its unit digit
Problem 12
If \(a: b=2: 3, b: c=4: 5\) and \(a+c=736\), then the value of \(b\) is
A) 392
B) 378
C) 384
D) 386
Problem 13
In the given figure,
\[
\begin{aligned}
& \angle B=110^{\circ} ; \quad \angle C=80^{\circ} ; \
& \angle F=120^{\circ} ; \quad \angle A D C=30^{\circ} \
& 2 \angle D G F=\angle D E F .
\end{aligned}
\]
The measure of \(\angle B H F\) is
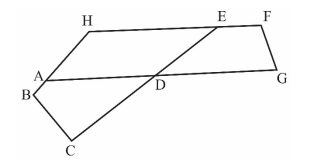
A) \(115^{\circ}\)
B) \(135^{\circ}\)
C) \(100^{\circ}\)
D) \(130^{\circ}\)
Problem 14
If \(\frac{1}{b+c}+\frac{1}{c+a}=\frac{2}{a+b}\), then the value of \(\frac{a^2+b^2}{c^2}\) is
A) 2
B) 1
C) 1 / 2
D) 3
Problem 15
If 3 men or 4 women can do a job in 43 days, the number of days the same job is done by 7 men and 5 women is
A) 12
B) 10
C) 11
D) 13
Problem 16
The expression \(49(a+b)^2-46(a-b)^2\) is factorized into \((l a+m b)(n a+p b)\), then the numerical value of \((l+m+n+p)\) is _________________
Problem 17
The integer part of the solution of the equation in \(x\), \(\frac{1}{3}(x-3)-\frac{1}{4}(x-8)=\frac{1}{5}(x-5)\) is ______________
Problem 18
In the adjoining figure, \(A B C\) is a triangle in which \(\angle B A C=100^{\circ}\), \(\angle A C B=30^{\circ}\). An equilateral triangle, a square and a regular hexagon are drawn as shown in the figure. The measure (in degrees) of \((x+y+z)\) is ____________
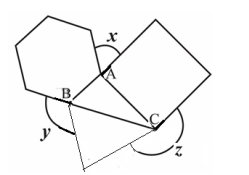
Problem 19
The mean of 5 numbers is 105 . The first number is \(\frac{2}{5}\) times the sum of the other 4 numbers. The first number is ____________
Problem 20
\(P Q R S\) is a square. The sides \(P Q\) and \(R S\) are increased by 30 % each and the sides \(Q R\) and \(P S\) are increased by 20 % each. The area of the quadrilateral thus obtained exceeds the area of the square by ___________ %.
Problem 21
If \(x^2+(2+\sqrt{3}) x-1=0\) and \(x^2+\frac{1}{x^2}=a+b \sqrt{c}\), then \((a+b+c)\) is _____________
Problem 22
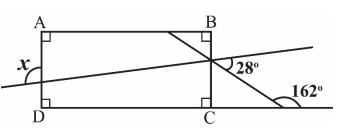
In the given figure, \(A B C D\) is a rectangle.
The measure of angle \(x\) is _________________ degrees.
Problem 23
The sum of all positive integers \(m, n\) which satisfy \(m^2+2 m n+n=44\) is __________________
Problem 24
Given \(a=2025, b=2024\), the numerical value of \(\left(a+b-\frac{4 a b}{a+b}\right) \div\left(\frac{a}{a+b}-\frac{b}{b-a}+\frac{2 a b}{b^2-a^2}\right)\) is _________________
Problem 25
In the sequence \(0,7,26,63,124, \ldots \ldots \ldots\) the \(6^{\text {th }}\) term is _____________
Problem 26
\[
\text { If } A=\sqrt{281+\sqrt{53+\sqrt{112+\sqrt{81}}}}, B=\sqrt{92+\sqrt{55+\sqrt{75+\sqrt{36}}}}
\]
then \(A-B\) is _______________________
Problem 27
The average of the numbers \(a, b, c, d\) is \((b+4)\). The average of pairs \((a, b),(b, c)\) and \((c, a)\) are respectively 16,26 and 25 . Then the average of \(d\) and 67 is ___________________
Problem 28
\(A B C\) is a quadrant of a circle of radius 10 cm . Two semicircles are drawn as in the figure.
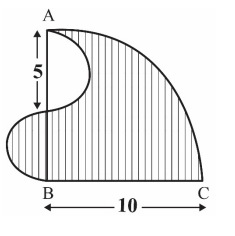
The area of the shaded portion is \(k \pi\), where \(k\) is a positive integer.
The value of \(k\) is __________________
Problem 29
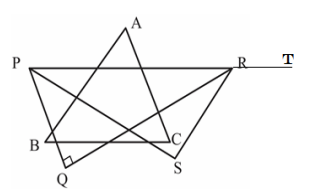
In the figure, \(A B C\) and \(P Q R\) are two triangles such that \(\angle \mathrm{A}: \angle \mathrm{B}: \angle \mathrm{C}=5: 6: 7\) and \(\angle P R Q=\angle B\). \(P S\) makes an angle \(\frac{\angle P}{3}\) with \(P Q\) and \(R S\) makes an angle \(\frac{\angle S R T}{5}\) with \(R Q\). Then the measure of \(\angle S\) is ______________________
Problem 30
In a two-digit positive integer, the units digit is one less than the tens digit. The product of one less than the units digit and one more than the tens digit is 40. The number of such two-digit integers is _______________