The greatest 4 -digit number such that when divided by 16,24 and 36 leaves 4 as remainder in each case is
А) 9994
B) 9940
C) 9094
D) 9904
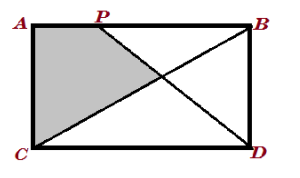
\(A B C D\) is a rectangle whose length \(A B\) is 20 units and breadth is 10 units. Also, given \(A P=8\) units. The area of the shaded region is \(\frac{p}{q}\) sq unit, where \(p, q\) are natural numbers with no common factors other than 1 . The value of \(p+q\) is
A) 167
В) 147
C) 157
D) 137
The solution of \(\frac{\sqrt[7]{12+x}}{x}+\frac{\sqrt[7]{12+x}}{12}=\frac{64}{3}(\sqrt[7]{x})\) is of the form \(\frac{a}{b}\) where \(a, b\) are natural numbers with \(\operatorname{GCD}(a, b)=1\); then \((b-a)\) is equal to
A) 115
B) 114
C) 113
D) 125
The value of \((52+6 \sqrt{43})^{3 / 2}-(52-6 \sqrt{43})^{3 / 2}\) is
A) 858
В) 918
C) 758
D) 828
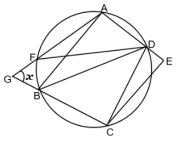
In the adjoining figure \(\angle D C E=10^{\circ}\), \(\angle C E D=98^{\circ}, \angle B D F=28^{\circ}\)
Then the measure of angle \(x\) is
A) \(72^{\circ}\)
B) \(76^{\circ}\)
C) \(44^{\circ}\)
D) \(82^{\circ}\)
\(A B C\) is a right triangle in which \(\angle \mathrm{B}=90^{\circ}\). The inradius of the triangle is \(r\) and the circumradius of the triangle is R . If \(\mathrm{R}: r=5: 2\), then the value of \(\cot ^2 \frac{A}{2}+\cot ^2 \frac{C}{2}\) is
A) \(\frac{25}{4}\)
B) 17
C) 13
D) 14
If \((\alpha, \beta)\) and \((\gamma, \beta)\) are the roots of the simultaneous equations:
\[
|x-1|+|y-5|=1 ; \quad y=5+|x-1|
\]
then the value of \(\alpha+\beta+\gamma\) is
A) \(\frac{15}{2}\)
B) \(\frac{17}{2}\)
C) \(\frac{14}{3}\)
D) \(\frac{19}{2}\)
Three persons Ram, Ali and Peter were to be hired to paint a house. Ram and Ali can paint the whole house in 30 days, Ali and Peter in 40 days while Peter and Ram can do it in 60 days. If all of them were hired together, in how many days can they all three complete $50 \%$ of the work?
A) $24 \frac{1}{3}$
B) $25 \frac{1}{2}$
C) $26 \frac{1}{3}$
D) $26 \frac{2}{3}$
$\frac{\sqrt{a+3 b}+\sqrt{a-3 b}}{\sqrt{a+3 b}-\sqrt{a-3 b}}=x$, then the value of $\frac{3 b x^2+3 b}{a x}$ is
A) 1
B) 2
C) 3
D) 4
The number of integral solutions of the inequation $\left|\frac{2}{x-13}\right|>\frac{8}{9}$ is
A) 1
B) 2
C) 3
D) 4
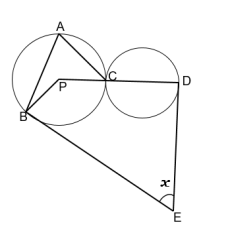
In the adjoining figure, $P$ is the centre of the first circle, which touches the other circle in C . PCD is along the diameter of the second circle. $\angle \mathrm{PBA}=20^{\circ}$ and $\angle \mathrm{PCA}=30^{\circ}$.
The tangents at B and D meet at E . The measure of the angle $x$ is
A) $75^{\circ}$
B) $80^{\circ}$
C) $70^{\circ}$
D) $85^{\circ}$
If $\alpha, \beta$ are the values of $x$ satisfying the equation $3 \sqrt{\log _2 x}-\log _2 8 x+1=0$, where $\alpha<\beta$, then the value of $\left(\frac{\beta}{\alpha}\right)$ is
A) 2
B) 4
C) 6
D) 8
When a natural number is divided by 11 , the remainder is 4 . When the square of this number is divided by 11 , the remainder is
A) 4
B) 5
C) 7
D) 9
The unit's digit of a 2-digit number is twice the ten's digit. When the number is multiplied by the sum of the digits the result is 144 . For another 2-digit number, the ten's digit is twice the unit's digit and the product of the number with the sum of its digits is 567 . Then the sum of the two 2 -digit numbers is
A) 68
В) 86
C) 98
D) 87
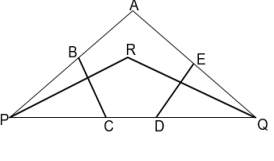
$A B C D E$ is a pentagon. $\angle A E D=126^{\circ}, \angle B A E=\angle C D E$ and $\angle A B C$ is $4^{\circ}$ less than $\angle B A E$ and $\angle B C D$ is $6^{\circ}$ less than $\angle C D E . P R, Q R$ the bisectors of $\angle B P C, \angle E Q D$ respectively, meet at $R$. Points $\mathrm{P}, \mathrm{C}, \mathrm{D}, \mathrm{Q}$ are collinear. Then measure of $\angle P R Q$ is
A) $151^{\circ}$
B) $137^{\circ}$
C) $141^{\circ}$
D) $143^{\circ}$
$a, b, c$ are real numbers such that $b-c=8$ and $b c+a^2+16=0$.
The numerical value of $a^{2025}+b^{2025}+c^{2025}$ is $\rule{2cm}{0.2mm}$.
Given $f(x)=\frac{2025 x}{x+1}$ where $x \neq-1$. Then the value of $x$ for which $f(f(x))=(2025)^2$ is $\rule{2cm}{0.2mm}$.
The sum of all the roots of the equation $\sqrt[3]{16-x^3}=4-x$ is $\rule{2cm}{0.2mm}$.
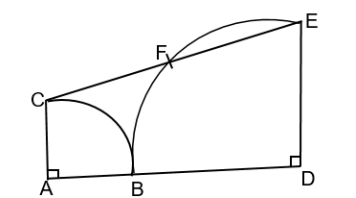
In the adjoining figure, two
Quadrants are touching at $B$.
$C E$ is joined by a straight line, whose mid-point is $F$.
The measure of $\angle C E D$ is $\rule{2cm}{0.2mm}$.
The value of $k$ for which the equation $x^3-6 x^2+11 x+(6-k)=0$ has exactly three positive integer solutions is $\rule{2cm}{0.2mm}$.
The number of 3-digit numbers of the form $a b 5$ (where $a, b$ are digits) which are divisible by 9 is $\rule{2cm}{0.2mm}$.
If $a=\sqrt{(2025)^3-(2023)^3}$, the value of $\sqrt{\frac{a^2-2}{6}}$ is $\rule{2cm}{0.2mm}$.
In a math Olympiad examination, $12 \%$ of the students who appeared from a class did not solve any problem; $32 \%$ solved with some mistakes. The remaining 14 students solved the paper fully and correctly. The number of students in the class is $\rule{2cm}{0.2mm}$.
When $a=2025$, the numerical value of
$\left|2 a^3-3 a^2-2 a+1\right|-\left|2 a^3-3 a^2-3 a-2025\right|$ is $\rule{2cm}{0.2mm}$.
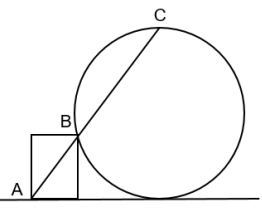
A circular hoop and a rectangular frame are standing on the level ground as shown. The diagonal $A B$ is extended to meet the circular hoop at the highest point $C$. If $A B=18 \mathrm{~cm}, B C=32 \mathrm{~cm}$, the radius of the hoop (in cm ) is $\rule{2cm}{0.2mm}$.
' $n$ ' is a natural number. The number of ' $n$ ' for which $\frac{16\left(n^2-n-1\right)^2}{2 n-1}$ is a natural number is $\rule{2cm}{0.2mm}$.
The number of solutions $(x, y)$ of the simultaneous equations $\log _4 x-\log _2 y=0, \quad x^2=8+2 y^2$ is $\rule{2cm}{0.2mm}$.
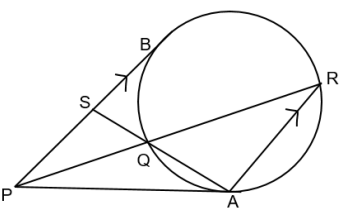
In the adjoining figure,
$P A, P B$ are tangents.
$A R$ is parallel to $P B$
$P Q=6 ; Q R=18 .$
Length $S B= \rule{2cm}{0.2mm}$.
A large watermelon weighs 20 kg with $98 \%$ of its weight being water. It is left outside in the sunshine for some time. Some water evaporated and the water content in the watermelon is now $95 \%$ of its weight in water. The reduced weight in kg is $\rule{2cm}{0.2mm}$.
In a geometric progression, the fourth term exceeds the third term by 24 and the sum of the second and third term is 6 . Then, the sum of the second, third and fourth terms is $\rule{2cm}{0.2mm}$.