Circle Problem | AMC 10A, 2006 | Problem 23

Try this beautiful problem from Geometry: Circle

Circle Problem - AMC-10A, 2006- Problem 23

Circles with centers $A$ and $B$ have radii 3 and 8 , respectively. A common internal tangent intersects the circles at $C$ and $D$, respectively. Lines $A B$ and $C D$ intersect at $E,$ and $A E=5 .$ What is $C D ?$

,

i

$13$
$\frac{44}{3} $
$\sqrt{221}$
$\sqrt{255}$
$\frac{55}{3}$

Key Concepts

Geometry

Circle

Tangents

Check the Answer

Answer: $ \frac{44}{3}$

AMC-10 (2006) Problem 23

Pre College Mathematics

Try with Hints

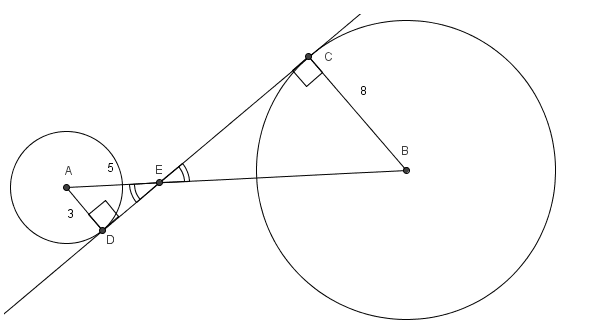
Given that Circles with centers $A$ and $B$ have radii 3 and 8 and $A E=5 .$.we have to find out $CD$.So join $BC$ and $AD$.then clearly $\triangle BCE$ and $\triangle ADE$ are Right-Triangle(as $CD$ is the common tangent ).Now $\triangle BCE$ and $\triangle ADE$ are similar.Can you proof $\triangle BCE$ and $\triangle ADE$?

Can you now finish the problem ..........

$\angle A E D$ and $\angle B E C$ are vertical angles so they are congruent, as are angles $\angle A D E$ and $\angle B C E$ (both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus, $\triangle A C E \sim \triangle B D E$.

By the Pythagorean Theorem, line segment $DE=4$

Therefore from the similarity we can say that $\frac{D E}{A D}=\frac{C E}{B C} \Rightarrow \frac{4}{3}=\frac{C E}{8}$ .

Therefore $C E=\frac{32}{3}$

can you finish the problem........

Therefore $CD=CE+DE=4+\frac{32}{3}=\frac{44}{3}$

Circle Problem | AMC 10A, 2006 | Problem 23