Try this beautiful problem from Singapore Mathematics Olympiad based on Area of Circle.
On the xy - plane , let S denote the region consisting of all points
(x,y ) for which \(|x+ \frac {1}{2} y | \leq 10 \) and \(|x|\leq 10 \) and \(|y|\leq 10 \). The largest circle centered at ( 0,0 ) that can be fitted in the region S has area \(k\pi\). Find the value of k.
Area of Circle
2 D Geometry
Answer: 80.
Singapore Mathematics Olympiad - 2013 - Senior Section - Problem No. 14
Challenges and Thrills - Pre - College Mathematics
We can start the sum from here :
The region S is the hexagon enclosed by lines
\(x = \pm 10 \) ; \( y = \pm 10 \) and \( x + \frac {1}{2} y = \pm 10\).
So the largest circle contained in S must be tangent to \(x + \frac {1}{2} y = \pm 10\)
Try to find the radius from this ....................
We can start this hint by using a diagram:
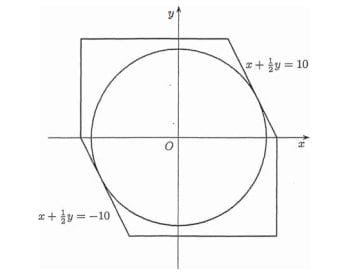
So following the last hint we can understand that its radius is the distance from the origin (0,0) to \( x + \frac {1}{2} y = 10 \)
r = \( \frac {10}{ \sqrt {1+ ({\frac {1}{2}})^2}} = 4\sqrt {5} \).
Now it very easy to find the rest of the solutiion.........
So the area of a circle is \(\pi {r}^2\)
= \(\pi {(4\sqrt 5)}^2 \)
= \(80 \pi\) (Answer).