Angles of Star | AMC 8, 2000 | Problem 24

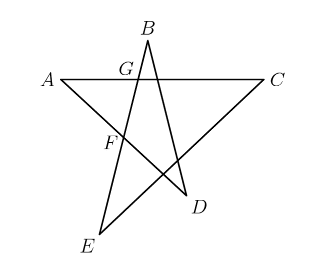
If \(\angle A = 20^\circ\) and \(\angle AFG =\angle AGF\), then \(\angle B+\angle D =\)

Find the \(\angle AFG\)

Can you now finish the problem ..........

sum of the angles of a Triangle is \(180^\circ\)

can you finish the problem........

we know that the sum of the angles of a Triangle is \(180^\circ\)

In the \(\triangle AGF\) we have,\((\angle A +\angle AGF +\angle AFG) =180^\circ \)

\(\Rightarrow 20^\circ +2\angle AFG=180^\circ\)(as \(\angle A =20^\circ\) & \(\angle AFG=\angle AGF\))

\(\Rightarrow \angle AFG=80^\circ\) i.e \(\angle EFD=\angle 80^\circ\)

So the \(\angle BFD=\frac{360^\circ -80^\circ-80^\circ}{2}=100^\circ\)

Now in the \(\triangle BFD\),\((\angle BFD +\angle B +\angle D\))=\(180^\circ\)

\(\Rightarrow \angle B +\angle D=180^\circ -100^\circ\)

\(\Rightarrow \angle B +\angle D=80^\circ\)

AMC - AIME Boot Camp... for brilliant students.

Use our exclusive one-on-one plus group class system to prepare for Math Olympiad

Learn More

Subscribe to Cheenta at Youtube