Research Track - Cocompact action and isotropy subgroups

In mathematics, if the quotient space X/G is a compact space, then it is called cocompact action of a group G on a topological space X. If X is locally compact, then an equivalent condition is that there is a compact subset K of X such that the image of K under the action of G covers X.

Suppose a group $latex \Gamma $ is acting properly and cocompactly on a metric space X, by isometries.

(Understand: proper, cocompact, isometric action)

Claim

There are only finitely many conjugacy classes of the isotropy subgroups in $latex \Gamma $

Sketch

Since the action is cocompact, there is a compact set K whose translates cover X.

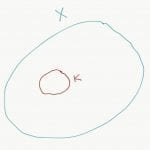
For each $latex x \in K $, choose small (enough) balls $latex B_x $.

How small do we want the balls?

Small enough, such that all but finitely many of the translates of the ball is disjoint from the ball.

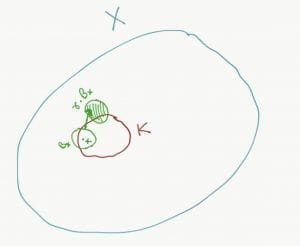
In the picture, the green blob around x in K is an example of $latex B_x $ . It is small enough such that $latex \gamma \cdot B_x $ is disjoint from $latex B_x $. The ball $latex B_x $ is small enough such that most almost $latex \gamma $ this should happen (except finitely many of them).

How do we know that there is such a ball? This is by definition of proper action. Since the action is proper, by definition, we will get such balls for each x in X.

Intuitively a proper action is proper, that is, most of them (the isometries) move balls considerably.

Examples to keep in mind: Integer translation on the real line is proper. Rational translation on the real line is not proper.

$latex \cup B_x $ is an open cover of K. Hence it has a finite subcover (as K is compact).

Choose finitely many balls $latex B_{x_1}, \cdots , B_{x_k} $, such that they cover K.

These finitely many balls have two properties:

1. They cover K
2. $latex \gamma \cdot B_{x_i} \cap B_{x_i} \neq \phi $ for finitely many $latex \gamma \in \Gamma $

Suppose $latex \displaystyle { \Sigma = \{ \gamma | \gamma \cdot B_{x_i} \cap B_{x_i} \neq \phi \} } $

Thus each member of $latex \Sigma $ has this property : hit all of the balls in the previously found cover by it. At least one of them will not move a lot (that is the translate will have a non-empty intersection with the ball)

Also notice that $latex \Sigma $ is finite (as there are finitely many balls and for each ball there are finitely many $latex \gamma $.

Suppose $latex x \in X $ be any point. There is a $latex \gamma \in \Gamma $ such that $latex x \in \gamma \cdot K $.

Then $latex \gamma^{-1} \cdot x \in K $ . This is the element of K that goes to x under $latex \gamma $

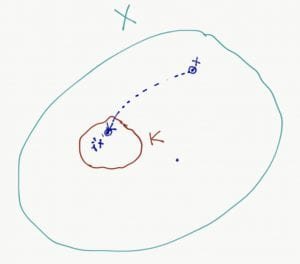
Now consider the isotropy subgroup $latex \Gamma_x $, that is group of all isometries that fixes x.

Notice that $latex \gamma^{-1} \Gamma_x \gamma $ is the isotropy subgroup of $latex \gamma^{-1} \cdot x $. Why? Suppose $latex \gamma_1 \in \Gamma_x $. We will show that $latex \gamma^{-1} \gamma_1 \gamma ) fixes ( \gamma^-1 \cdot x $.

After all $latex \gamma^{-1} \gamma_1 \gamma ( \gamma^{-1} \cdot x)  = \gamma^{-1} \cdot x $

We can similarly show the converse.

Hence we have shown that if x is pulled back into K by some $latex \gamma^{-1} $ conjugating the isotropy subgroup of x by that $latex \gamma $ gives the isotropy subgroup of the pulled back element.

But this is the subgroup that does not move the ball in the cover containing $latex \gamma^{-1} \cdot x $ in a disjoint manner. Hence it must be inside $latex \Sigma $, and hence finite as $latex \Sigma $ was finite.