Which of the following is true?
(A) \(\sin \left(105^{\circ}\right)-\cos \left(105^{\circ}\right)=\frac{\sqrt{3}}{2}\)
(B) \(\sin \left(105^{\circ}\right)-\cos \left(105^{\circ}\right)=\frac{\sqrt{3}}{\sqrt{2}}\)
(C) \(\sin \left(105^{\circ}\right)+\cos \left(105^{\circ}\right)=\frac{1}{2}\)
(D) \(\sin \left(105^{\circ}\right)+\cos \left(105^{\circ}\right)=\frac{1}{\sqrt{3}}\)
(E) None of the above.
Suppose \(\cos \left(180^{\circ}+x\right)=\frac{4}{5}\), where \(90^{\circ}<x<180^{\circ}\). Find \(\tan (2 x)\).
(A) \(\frac{24}{7}\)
(B) \(\frac{7}{24}\)
(C) \(-\frac{24}{7}\)
(D) \(-\frac{7}{24}\)
(E) \(-\frac{24}{25}\)
Let \(x\) be a real number such that
\(\frac{\sin ^4 x+\cos ^4 x}{\sin ^2 x+\cos ^4 x}=\frac{8}{11}\) .
Assuming \(\sin ^2 x>\frac{1}{2}\), find the value of \(\sqrt{28}\left(\sin ^4 x-\cos ^4 x\right)\).
Let \(C\) be a constant such that the equation \(5 \cos x+6 \sin x-C=0\) have two distint roots \(a\) and \(b\), where \(0<b<a<\pi\). Find the value of \(61 \times \sin (a+b)\).
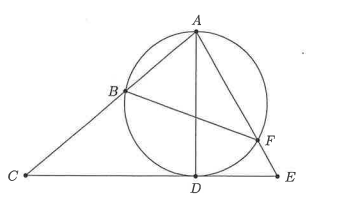
In the diagram below, \(C E\) is tangent to the circle at point \(D, A D\) is a diameter of the circle, and \(A B C, A F E\) are straight lines. It is given that \(\frac{A B}{A C}=\frac{16}{41}\) and \(\frac{A F}{A E}=\frac{49}{74}\). Let \(\tan (\angle C A E)=\frac{m}{n}\), where \(m, n\) are positive integers and \(\frac{m}{n}\) is a fraction in its lowest form. Find the sum \(m+n\).
Let \(f(x)=\cos ^2\left(\frac{\pi x}{2}\right)\). Find the value of
\(f \left(\frac{1}{2023}\right)+f\left(\frac{2}{2023}\right)+\cdots+f\left(\frac{2021}{2023}\right)+f\left(\frac{2022}{2023}\right)\) .
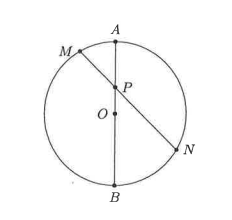
In the diagram below, \(A B\) is a diameter of the circle with centre \(O, M N\) is a chord of the circle that intersects \(A B\) at \(P, \angle B O N\) and \(\angle M O A\) are acute angles, \(\angle M P A=45^{\circ}\), \(M P=\sqrt{56}\), and \(N P=12\). Find the radius of the circle.
Let \(\triangle A B C\) be an equilateral triangle. \(D, E, F\) are points on the sides such that
\(B D: D C=C E: E A=A F: F B=2: 1\) .
Suppose the area of the triangle bounded by \(A D, B E\) and \(C F\) is \(2023\) . Find the area of \(\triangle A B C\).

Find the number of triangles such that all the sides are integers and the area equals the perimeter (in number).
Suppose \(y=\cos ^2 x-7 \cos x+25\), where \(x\) is any real number. Find the range of \(y\).
(A) \(17 \leq y \leq 33\)
(B) \(18 \leq y \leq 33\)
(C) \(19 \leq y \leq 33\)
(D) \(20 \leq y \leq 33\)
(E) None of the above
Suppose \(\sin \left(180^{\circ}+x\right)=-\frac{7}{9}\), where \(450^{\circ}<x<540^{\circ}\). Find \(\sin (2 x)\).
(A) \(\frac{49}{81} \sqrt{2}\)
(B) \(\frac{56}{81} \sqrt{2}\)
(C) \(-\frac{56}{81}\)
(D) \(-\frac{49}{81} \sqrt{2}\)
(E) \(-\frac{56}{81} \sqrt{2}\)
Find the value of
\(\left(\frac{\cos 10^{\circ}+\cos 50^{\circ}+\cos 70^{\circ}+\cos 110^{\circ}}{\cos 20^{\circ}}\right)^8\) .
Suppose
\(y=\frac{\tan ^2 x-\tan x+\sqrt{33}}{\tan ^2 x+\tan x+1}\),
where \(-90^{\circ}<x<90^{\circ}\). Find the maximum possible value of \(\sqrt{33}(y-5)\).
In the figure below, \(P Q R S\) is a square inscribed in a circle. Let \(W\) be a point on the arc \(P Q\) such that \(W S=\sqrt{20}\). Find \((W P+W R)^2\).

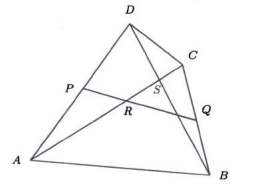
The figure below shows a quadrilateral \(A B C D\) such that \(A C=B D\) and \(P\) and \(Q\) are the midpoints of the sides \(A D\) and \(B C\) respectively. The lines \(P Q\) and \(A C\) meet at \(R\) and the lines \(B D\) and \(A C\) meet at (S). If \(\angle P R C=130^{\circ}\), find the angle \(\angle D S C\) in \({ }^{\circ})\).
Suppose
\(\cos x-\cos y =\frac{1}{2}\),
\(\sin x-\sin y =-\frac{1}{3}\)
If \(\sin (x+y)=\frac{m}{n})\), where \(\frac{m}{n}\) is expressed as a fraction in its lowest terms, find the value of \(m+n\).
Find the largest positive integer \(M\) such that \(\cos ^2 x-\sin ^2 x+\sin x=\frac{M}{888}\) has a real solution.
Which of the following is the largest?
(A) \(\tan 50^{\circ}+\sin 50^{\circ}\)
(B) \(\tan 50^{\circ}+\cos 50^{\circ}\)
(C) \(\sin 50^{\circ}+\cos 50^{\circ}\)
(D) \(\tan 50^{\circ}+\sin ^2 50^{\circ}\)
(E) \(\sin ^2 50^{\circ}+\cos ^2 50^{\circ}\)
Suppose \(\sin \theta=\frac{n-3}{n+5}\) and \(\cos \theta=\frac{4-2 n}{n+5}\) for some integer \(n\). Find the maximum value of \(160 \tan ^2 \theta\).
(A) 80
(B) 90
(C) 100
(D) 120
(E) None of the above
If \(\cos A-\cos B=\frac{1}{2}\) and \(\sin A-\sin B=-\frac{1}{4}\), find the value of \(100 \sin (A+B)\).
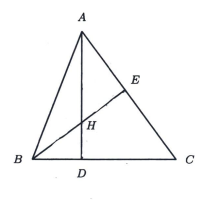
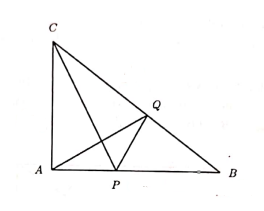
The figure below shows a triangle \(A B C\) such that \(A D\) and \(B E\) are altitudes to the sides \(B C\) and \(C A\) respectively. The lines \(A D\) and \(B E\) intersect at \(H\). Determine the area in \(\mathrm{cm}^2\) of the triangle \(A B C\) if \(A H=50 \mathrm{~cm}, D H=18 \mathrm{~cm}\) and \(B H=E H\).
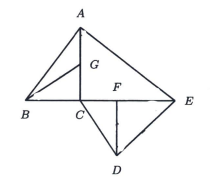
In the figure below, \(\angle G C B=\angle A C E=\angle D F E=90^{\circ}\), and \(\angle G B C=\angle E A C=\) \(\angle E D F=\theta^{\circ}\). Also, \(G B=6 \mathrm{~cm}, A E=10 \mathrm{~cm}\) and \(D E=8 \mathrm{~cm}\). Let \(\mathcal{S}\) denote the sum of the areas of the triangles \(A B C\) and \(C D E\). Find the maximum possible value of \(\mathcal{S}\) in \(\mathrm{cm}^2\) .
Find the minimum value of \(\frac{8}{\sin 2 \theta}+12 \tan \theta\), where \(0<\theta<\frac{\pi}{2}\).
Determine the largest angle \(\theta\) (in degree), where \(0^{\circ} \leq \theta \leq 360^{\circ}\), such that \(\sin \left(\theta+18^{\circ}\right)+\sin \left(\theta+162^{\circ}\right)+\sin \left(\theta+234^{\circ}\right)+\sin \left(\theta+306^{\circ}\right)=1+\cos \left(\theta+60^{\circ}\right)+\cos \left(\theta+300^{\circ}\right)\).
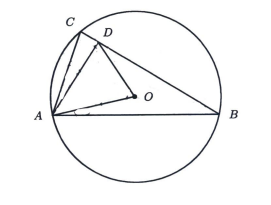
Let \(O\) be the circumcentre of the triangle \(A B C\) and that \(\angle A B C=30^{\circ}\). Let (D) be a point on the side (B C) such that the length of \(A D\) is the same as the radius of the circle. Determine the value of \(\angle A D O\) (in degree) if \(\angle O A B=10^{\circ}\).
Find the value of
\(\frac{1}{\sin ^2 0.5^{\circ}}-\tan ^2 0.5^{\circ}+\frac{1}{\sin ^2 1.5^{\circ}}-\tan ^2 1.5^{\circ}+\frac{1}{\sin ^2 2.5^{\circ}}-\tan ^2 2.5^{\circ}+\cdots+\frac{1}{\sin ^2 179.5^{\circ}}-\tan ^2 179.5^{\circ}\) .
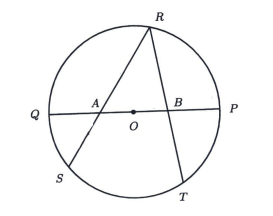
The figure below shows a circle centred at \(O\) with radius \(555 \mathrm{~cm}\). If \(O A=O B\) and \(\frac{R A}{A S}+\frac{R B}{B T}=\frac{13}{6}\), find \(O A\) (in cm).
Parallelogram \(A B C D\) has sides \(A B=39 \mathrm{~cm}\) and \(B C=25 \mathrm{~cm}\). Find the length of diagonal \(A C\) in \(\mathrm{cm}\) if diagonal \(B D=34 \mathrm{~cm}\).
Suppose \(\sin 45^{\circ}-x\)=\(-\frac{1}{3}\), where \(45^{\circ}<x<90^{\circ}\). Find \(6 \sin x-\sqrt{2})^2\).
If \(8 \cos x-8 \sin x=3\), find the value of \(55 \tan x+\frac{55}{\tan x}\).
The figure below shows a right-angled triangle \(A B C\) such that \(\angle B A C=90^{\circ}, \angle A B C=\) \(30^{\circ}\) and \(A B=48 \mathrm{~cm}\). Let \(P\) be a point on side \(A B\) such that \(C P\) is the angle bisector of \(\angle A C B\) and \(Q\) be a point on side \(B C\) such that line \(A Q\) is perpendicular to line \(C P\). Determine the length of \(P Q\).
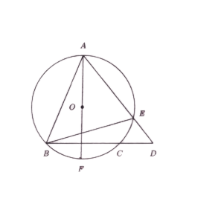
In the figure below, the point \(O\) is the center of the circle, \(A D\) and \(B C\) intersect at \(E\), and \(\angle A E B=70^{\circ}, \angle A O B=62^{\circ}\). Find the angle \(\angle O C D\left(\right.)\) in degree \(\left.{ }^{\circ}\right)\).
Find the value of \(\frac{4 \cos 43^{\circ}}{\sin 73^{\circ}}-\frac{12 \sin 43^{\circ}}{\sqrt{3} \sin 253^{\circ}}\).
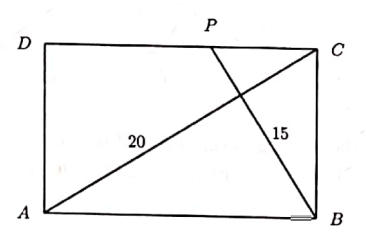
The figure below shows a rectangle (A B C D) such that the diagonal \(A C=20 \mathrm{~cm}\). Let (P) be a point on side \(C D\) such that \(B P\) is perpendicular to diagonal \(A C\). Find the area of rectangle \(A B C D\) \(in (\mathrm{cm}^2) \) if \(B P=15 \mathrm{~cm}\).
Find the number of non-congruent right-angled triangles such that the length of all their sides are integers and that the hypotenuse has a length of \(65 \mathrm{~cm}\).
Suppose that \(\sin x=\frac{12}{13}\) and \(\cos y=-\frac{4}{5}\), where \(0^{\circ} \leq x \leq 90^{\circ}\) and \(90^{\circ} \leq y \leq 180^{\circ}\). Find the value of \(\cos (x+y)\).
(A) \(-\frac{56}{65}\)
(B) \(\frac{56}{65}\)
(C) \(-\frac{16}{65}\)
(D) \(\frac{16}{65}\)
(E) None of the above
Suppose \(\tan x=5\). Find the value of \(\frac{6+\sin 2 x}{1+\cos 2 x}\).
The coordinates of the vertices of a triangle \(\triangle A B C\) are \(A(6,0), B(0,8)\) and \(C(x, y)\) such that \(x^2-16 x+y^2-12 y+91=0\). Find the largest possible value of the area of the triangle \(\triangle A B C\).
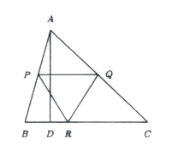
In the figure below, \(A D\) is perpendicular to the \(B C, P Q\) is parallel to \(B C\), and the triangle \(\triangle P Q R\) is an equilateral triangle whose area in \(meter ^2\) is equal to the length of \(A D\) (in meter). Find the smallest possible value of the length of (B C).
Find the value of \(448\left(\frac{\sin 12^{\circ} \sin 39^{\circ} \sin 51^{\circ}}{\sin 24^{\circ}}\right)\).
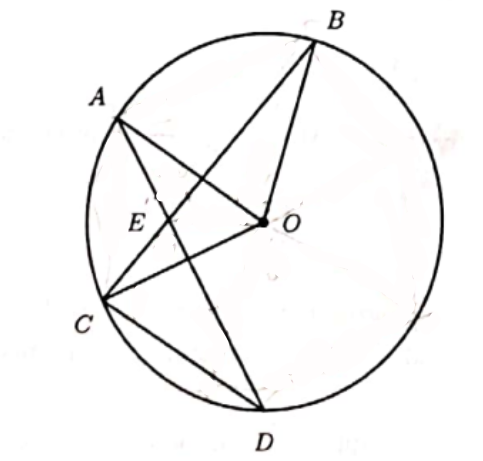
In the figure below, the chord \(A F\) passes through the origin \(O\) of the circle, and is perpendicular to the chord \(B C\). It is given that \(A B=17 \mathrm{~cm}, C D=5 \mathrm{~cm}\). Suppose \(\frac{B E}{E D}=\frac{m}{n}\), where \(m\) and \(n\) are positive integers which are relatively prime. What is the value of \(m+n\) ?
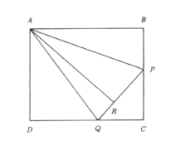
The figure below shows a rectangle \(A B C D\) with \(A B=16 \mathrm{~cm}) and (B C=15 \mathrm{~cm}\). Let \(P\) be a point on the side \(B C\) such that \(B P=7 \mathrm{~cm}\), and let \(Q\) be a point on the side \(C D\) such that \(C Q=6 \mathrm{~cm}\).
Find the length of \(A R\) \(in (\mathrm{cm})\), where \(R\) is the foot of the perpendicular from \(A\) to \(P Q\).
Consider a square \(A B C D\) on the \(x y\)-plane where the coordinates of its vertices are given by \(A(13,0), B(23,13), C(10,23)\) and \(D(0,10)\). A lattice point is a point with integer coordinates. Find the number of lattice points in the interior of the square.