Volume of revolution : IIT JAM 2018 Question Number 19

Competency in Focus: Application of Calculus (Volume of Revolution)
This problem is from IIT JAM 2018 (Question number 19) and is based on the calculation of the volume of revolution.

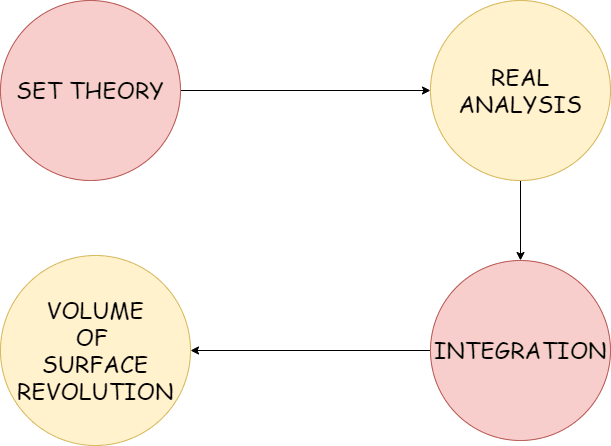
Consider the region (D) on (yz) plane and bounded by the line (y=\frac{1}{2}) and the curve (y^{2}+z^{2}=1) where (y\geq0). If the region (D) is revolved about the (z-)axis then the volume of the resulting solid is
$ (A)\frac{\pi}{\sqrt{3}}\qquad$

$(B)\frac{2\pi}{\sqrt{3}} \qquad$

$(C)\frac{\pi\sqrt{3}}{2}\qquad$

$(D)\pi\sqrt{3} $

Do you really need a hint? Try it first!

Hint 1

Imagine that we have a portion of a curve.
$y=f(x)$ from $x=a$ to $x=b$.
In the $xy-plane$ we revolve it around a straight line - $x$-axis.
The result is called solid of revolution
Here in our next hint we will find techniques to calculate the volumes of solid of revolution.

Hint 2

Calculate the volumes of solid of revolution

Let's construct a narrow rectangle of base width $\mathrm d x$ and height $f(x)$ sitting under the curve. When this rectangle is revolved around the $x-\text{axis}$. We get a disk whose radius is $f(x)$ and height is $\mathrm d x$.
The volume of this disk $\mathrm d V=\pi[f(x)]^{2}\mathrm d x$.
So the total volume of the solid is
$V=\int_a^b \mathrm d V=\int_a^b \pi[f(x)]^{2}\mathrm d x$.
If the curve revolved around the vertical line (such as $y$-axis), then horizontal disks are used. If the curve can be solved for (x) in terms of (y). $x=g(y)$ then the formula would be.
$V=\int_a^b[g(y)]^2\mathrm d y$.
Now can you guess if the region between two curves is revolved around the axis.

HINT 3

Sometimes the region between two curves is revolved around the axis and a gap is created between the solid and the axis. A rectangle within the rotated region will become a disk with a hole in it, also known as washer. If the rectangle is vertical and extends from the curve $y=g(x)$ up to the curve $y=f(x)$, then when it is rotated around (x)- axis, it will result in a washer with volume equal to
$\mathrm d V=\pi{[f(x)]^{2}-[g(x)]^{2}}\mathrm d x$.
Which gives us
$V=\int_a^b \pi {[f(x)]^{2}-[g(x)]^{2}}\mathrm d x$.

HINT 4

Now in the given problem replace (x) by (z) , in the above discussion
$y=f(z)=\sqrt{1-z^{2}}, y=g(z)=\frac{1}{2}$
and the line $y=\frac{1}{2}$ intersects the curve at ( $\frac{-\sqrt{3}}{2},\frac{1}{2}$) , ( $\frac{\sqrt{3}}{2},\frac{1}{2}$) in terms of ($z,x)$ co-ordinate.
and hence the volume is
$V=\pi \int_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}}[(1-z^{2})-\frac{1}{4})]\mathrm d z$.
$=\pi[\frac{3z}{4}-\frac{z^{3}}{3}]_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}}$
$=\pi(\frac{3\sqrt{3}}{8}-\frac{3\sqrt{3}}{24})\times 2$
$=\pi \frac{3\sqrt{3} \times 2 \times 2}{24}$
$=\frac{\pi \sqrt{3}}{2}$