Unlocking the Curious Combination of Number Theory and Algebra: ISI Entrance Problem, TOMATO Subjective 17
Join Trial or Access Free ResourcesJoin Trial or Access Free ResourcesLets dive into a captivating problem that unites algebra and number theory, creating a compelling challenge. This puzzle revolves around a particular type of mathematical equation. The ultimate aim is to prove that the solutions to this equation cannot be expressed as straightforward fractions like 1/2 or 3/4.
Here is the question we solve:
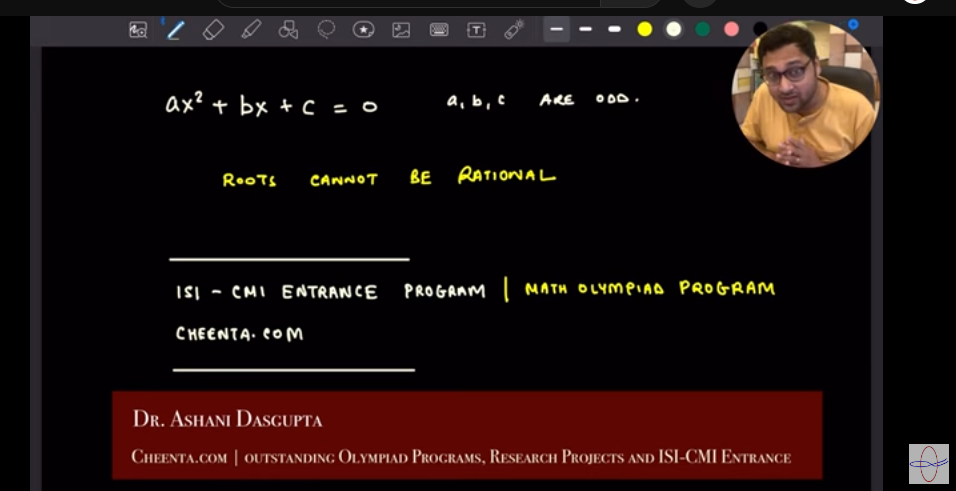
If the coefficients of a quadratic equation
are all odd integers, show that the roots cannot be rational.
To solve this problem we use the quadratic formula and a clever concept known as "parity check." At the heart of the matter is demonstrating that the discriminant, b² - 4ac, doesn't fit the definition of a "perfect square."
Now, let's delve into the parity check. Regardless of the interplay between even and odd numbers, the left side of the equation consistently maintains an even quality, while the right side remains steadfastly odd. This leads to a conclusion: the solutions do not exist
In 2026, the following Cheenta students have been successful for Indian Statistical Institute's M.Stat Entrance. They ranked within the first 50 in the entire country in these entrances. I.S.I. M.Stat Entrance
In 2026, the following Cheenta students have been successful for Indian Statistical Institute's B.Stat Entrance and Chennai Mathematical Institute's B.Sc. Math Entrance. They ranked within the first 200 in the entire country in these entrances. Most of these students attended the problem solving workshops regularly, which happen 5 days every week. CMI B.Sc. Math Entrance […]
In 2025, 8 students from Cheenta Academy cracked the prestigious Regional Math Olympiad. In this post, we will share some of their success stories and learning strategies. The Regional Mathematics Olympiad (RMO) and the Indian National Mathematics Olympiad (INMO) are two most important mathematics contests in India.These two contests are for the students who are […]
Cheenta Academy proudly celebrates the success of 27 current and former students who qualified for the Indian Olympiad Qualifier in Mathematics (IOQM) 2025, advancing to the next stage — RMO. This accomplishment highlights their perseverance and Cheenta’s ongoing mission to nurture mathematical excellence and research-oriented learning.