The roots of the quadratic equation \(x^2-7 m x+5 n=0\) are \(m\) and \(n\), where \(m \neq 0\) and \(n \neq 0\). Find a quadratic equation whose roots are \(\frac{m}{n}\) and \(\frac{n}{m}\).
(A) \(6 x^2-37 x+1=0\)
(B) \(6 x^2-50 x-7=0\)
(C) \(6 x^2-50 x+7=0\)
(D) \(6 x^2-37 x+6=0\)
(E) \(x^2-37 x+1=0\)
Simplify
\[
(\sqrt{10}-\sqrt{2})^{\frac{1}{3}}(\sqrt{10}+\sqrt{2})^{\frac{7}{3}} .
\]
(A) \(24+4 \sqrt{5}\)
(B) \(24+6 \sqrt{5}\)
(C) \(24+8 \sqrt{5}\)
(D) \(24+10 \sqrt{5}\)
(E) \(24+12 \sqrt{5}\)
Let \(a=4^{3000}, b=6^{2500}\) and \(c=7^{2000}\). Which of the following statement is true?
(A) \(a<b<c\)
(B) \(a<c<b\)
(C) \(b<a<c\)
(D) \(c<a<b\)
(E) \(c<b<a\)
If \(\log _{21} 3=x\), express \(\log _7 9\) in terms of \(x\).
(A) \(\frac{2 x}{2-x}\)
(B) \(\frac{2 x}{1-x}\)
(C) \(\frac{2 x}{x-2}\)
(D) \(\frac{2 x}{x-1}\)
(E) \(\frac{x}{1-x}\)
Suppose that \(\sin x=\frac{12}{13}\) and \(\cos y=-\frac{4}{5}\), where \(0^{\circ} \leq x \leq 90^{\circ}\) and \(90^{\circ} \leq y \leq 180^{\circ}\). Find the value of \(\cos (x+y)\).
(A) \(-\frac{56}{65}\)
(B) \(\frac{56}{65}\)
(C) \(-\frac{16}{65}\)
(D) \(\frac{16}{65}\)
(E) None of the above
Find the largest positive integer (n) such that (n+8) is a factor of \(n^3+13 n^2+40 n+40\).
Suppose \(\tan x=5\). Find the value of \(\frac{6+\sin 2 x}{1+\cos 2 x}\).
Suppose (x) and (y) are real numbers such that
\[
|x-y|+3 x-y=70, \text { and } \
|y-x|+3 y+x=50 .
\]
Find the maximum possible value of \(x+2 y\).
The coordinates of the vertices of a triangle \(\triangle A B C\) are \(A(6,0), B(0,8)\) and \(C(x, y)\) such that \(x^2-16 x+y^2-12 y+91=0\). Find the largest possible value of the area of the triangle \(\triangle A B C\).
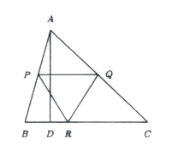
In the figure below, \(A D\) is perpendicular to the \(B C, P Q\) is parallel to \(B C\), and the triangle \(\triangle P Q R\) is an equilateral triangle whose area in \(meter ^2\) is equal to the length of \(A D\) (in meter). Find the smallest possible value of the length of (B C).
Find the value of \(448\left(\frac{\sin 12^{\circ} \sin 39^{\circ} \sin 51^{\circ}}{\sin 24^{\circ}}\right)\).
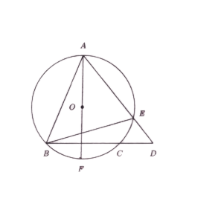
In the figure below, the chord \(A F\) passes through the origin \(O\) of the circle, and is perpendicular to the chord \(B C\). It is given that \(A B=17 \mathrm{~cm}, C D=5 \mathrm{~cm}\). Suppose \(\frac{B E}{E D}=\frac{m}{n}\), where \(m\) and \(n\) are positive integers which are relatively prime. What is the value of \(m+n\) ?
Let \(P(x)\) be the polynomial that results from the expansion of the following expression:
\[
\left(2 x^3+3 x^2+x\right)^5\left(\frac{x}{6}+\frac{1}{2}\right)^5 .
\]
Find the sum of the coefficients of \(x^{2 k+1}\), where \(k=0,1,2,3, \ldots, 9\).
Find the value of the following expression:
\[
\frac{2\left(1^2+2^2+3^2+\ldots+49^2+50^2\right)+(1 \times 2)+(2 \times 3)+(3 \times 4)+\ldots+(48 \times 49)+(49 \times 50)}{100} .
\]
Let \(M\) be the maximum possible value of \(\frac{15 x^2-x^3-39 x-54}{x+1}\), where \(x\) is a positive integer. Find the value of \(9 M\).
Find the maximum possible value of \(x+y+z\) where \(x, y, z\) are integers satisfying the following system of equations:
\[
x^2 z+y^2 z+8 x y=200 \
2 x^2+2 y^2+x y z=50 .
\]
Find the remainder when \(10^{43}\) is divided by \(126\) .
Suppose \(\left(\log _2 x\right)^2\)+\(4\left(\log _2\left(\log _3 y\right)\right)^2\) = \(4\left(\log _2 x\right)\left(\log _2\left(\log _3 y\right)\right)\). If \(x = 49\) and \(y\) is a positive integer, find \(y\).
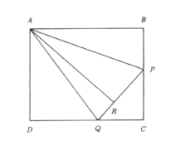
The figure below shows a rectangle \(A B C D\) with \(A B=16 \mathrm{~cm}) and (B C=15 \mathrm{~cm}\). Let \(P\) be a point on the side \(B C\) such that \(B P=7 \mathrm{~cm}\), and let \(Q\) be a point on the side \(C D\) such that \(C Q=6 \mathrm{~cm}\).
Find the length of \(A R\) \(in (\mathrm{cm})\), where \(R\) is the foot of the perpendicular from \(A\) to \(P Q\).
A sequence \(x_0, x_1, x_2, x_3, \ldots\) of integers satisfies the following conditions: \(x_0=1\), and for any positive integer \(n \geq 1,\left|x_n-1\right|=\left|x_{n-1}+2\right|\). Find the maximum possible value of \(2019-\left(x_1+x_2+\cdots+x_{2018}\right)\).
Consider a square \(A B C D\) on the \(x y\)-plane where the coordinates of its vertices are given by \(A(13,0), B(23,13), C(10,23)\) and \(D(0,10)\). A lattice point is a point with integer coordinates. Find the number of lattice points in the interior of the square.
Eleven distinct chemicals \(C_1, C_2, \ldots, C_{11}\) are to be stored in three different warehouses. Each warehouse stores at least one chemical. A pair \(C_i, C_j\) of chemicals, where \(i \neq j\), is either compatible or incompatible. Any two incompatible chemicals cannot be stored in the same warehouse. However, a pair of compatible chemicals may or may not be stored in the same warehouse. Find the maximum possible number of pairs of incompatible chemicals that can be found among the stored chemicals.
Let \(k\) be a positive integer and let the function \(f\) be defined as follows:
\[
f(x)=\frac{\pi^x}{\pi^x+\pi^{2 k-x}} .
\]
Suppose the function \(g(k)\) is defined as follows:
\[
g(k)=f(0)+f\left(\frac{k}{2019}\right)+f\left(\frac{2 k}{2019}\right)+f\left(\frac{3 k}{2019}\right)+\ldots+f\left(\frac{4037 k}{2019}\right)+f(2 k) .
\]
Find the greatest positive integer \(n\) such that \(g(k) \geq n\) for all \(k \geq 1\).
Some students sat for a test. The first group of students scored an average of 91 marks and were given Grade A. The second group of students scored an average of 80 marks and were given Grade B. The last group of students scored an average of 70 marks and were given Grade \(\mathrm{C}\). The numbers of students in all three groups are prime numbers and the total score of all the students is 1785 . Determine the total number of students.
Suppose (a) and (b) are positive integers satisfying
\(a^2-2 b^2=1\) .
If \(500<a+b<1000\), find \(a+b\).