In a certain company, one-third of the employees have a university degree. Half of the employees who have a university degree are men and \(40 \%\) of the employees who do not have a university degree are women. If 102 of the employees are men, how many of the employees are women?
(A) 58
(B) 78
(C) 98
(D) 108
(E) 118
How many non-congruent triangles with integer side lengths have perimeter 7 ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
The median and mean of five distinct numbers, (4,7,10,11, N), are equal. Find the sum of all possible values of (N).
(A) 18
(B) 21
(C) 26
(D) 29
(E) 35
The following diagram shows two semicircles whose diameters lie on the same line. (A B) is a chord of the larger semicircle that is tangent to the smaller semicircle at the point \(\mathrm{C}\) and is parallel to the diameter \(\mathrm{DE}\) of the larger semicircle. If \(|\mathrm{AB}|=16 \mathrm{~cm}\), what is the area of the shaded region in \(\mathrm{cm}^2\) ?
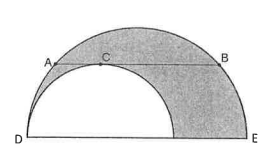
(A) \(8 \pi\)
(B) \(16 \pi\)
(C) \(32 \pi\)
(D) \(48 \pi\)
(E) \(64 \pi\)
The graph (not drawn to scale) of (y=a x^2+b x+c) with the maximum point at (x=-1) is shown below. Which of the following must be true?
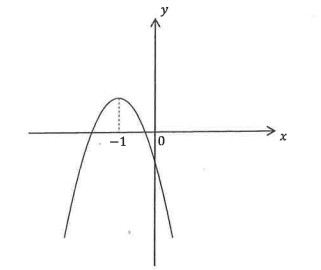
(I) (a-b+c>0)
(II) (a+b-c>0)
(III) (a b c>0)
(IV) (a b c<0)
(A) (I) and (IV)
(B) (II) and (IV)
(C) (I) and (III)
(D) (II) and (III)
(E) (I)
The product of the ages of three adults is 26390 . Find the sum of their ages. (A person is an adult if he or she is at least 21 years old.)
Let (n) be a positive integer such that (n+11) is a factor of (n^2+121). Find the largest possible value of (n).
Find the largest integer less than or equal to \((3+\sqrt{5})^3\).
The product of the two-digit number \(\overline{x 4}\) and the three-digit number \(\overline{3 y z}\) is 7656 . Find the value of (x+y+z).
If (x) and (y) are real numbers such that (x+y=12) and (x y=10), find the value of (x^4+y^4).
Let (a) and (b) be two positive integers such that \(a^2+4 b^2 \leq 1105\). Find the largest possible value of the product (a b).
Find the value of the integer (n) such that the following equation holds:
\([
\frac{\sqrt{5}+n \sqrt{3}-2 \sqrt{2}}{(\sqrt{5}+\sqrt{3})(\sqrt{3}-\sqrt{2})}=\sqrt{5}+\sqrt{2} .
]\)
The lengths of the sides of a triangle are \( \log_{10} 12\), \(\log_{10} 75\) and \(\log _{10}n\) where (n) is a positive integer. Find the number of possible values for (n).
Let (x) be a real number. What is the minimum value of the following expression?
\([
\frac{20 x^2+10 x+3}{2 x^2+x+1}
]\)
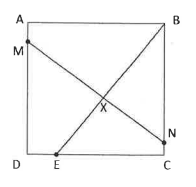
In the following diagram, \(\mathrm{ABCD}\) is a square of side \(16 \mathrm{~cm}\). \(\mathrm{E}\) lies on \(\mathrm{CD}\) such that \(|\mathrm{DE}|=) (4 \mathrm{~cm} . \mathrm{M}) and (\mathrm{N}\) lie on \(\mathrm{AD}\) and \(\mathrm{BC}\) respectively such that \(\mathrm{MN}\) is perpendicular to \(\mathrm{BE} . \mathrm{X}\) is the intersection of \(\mathrm{MN}\) and \(\mathrm{BE}). If (|\mathrm{MX}|=11 \mathrm{~cm}\) and \(|\mathrm{BN}|=x \mathrm{~cm}\), what is the value of (x) ?
Find the smallest positive integer (k) such that every subset of \({1,2, \ldots, 2023}\) with exactly (k) integers contains three integers (a, b, c) with (a<b<c) and (a b=c).
The difference between the least common multiple (LCM) and highest common factor (HCF) of a positive integer (n) and 18 is 627 . Find the value of (n).
The sum of all the interior angles except one of a convex polygon is \(2023^{\circ}\). What is the number of sides of this polygon? (A polygon is convex if every interior angle is between \(0^{\circ}\) and \(180^{\circ}).\)
If \(\sqrt{19-8 \sqrt{3}}\) is a root of the equation (x^2-a x+b=0) where (a) and (b) are rational numbers, find the value of (a+b).
Find the smallest positive integer (n) such that the equation (x^2+y^3=n^4) has a solution in positive integers (x) and (y).
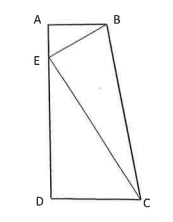
In the following diagram, (A B) is parallel to \(\mathrm{DC},|\mathrm{AB}|=6 \mathrm{~cm},|\mathrm{AD}|=17 \mathrm{~cm},|\mathrm{DC}|=10 \mathrm{~cm}\) and angle \(\mathrm{DAB}=90^{\circ}\). \(\mathrm{E}\) lies on \(\mathrm{AD}\) such that \(\mathrm{BE}\) is perpendicular to \(\mathrm{EC}\). If the area of triangle \(\mathrm{BEC}=k \mathrm{~cm}^2\), what is the largest possible value of (k) ?
The angle between the hour-hand and the minute-hand of a clock is denoted by \(\theta^{\circ}\) where \(0 \leq \theta \leq 180\). If the clock now shows (3: y) (that is, 3 o'clock and (y) minutes) and \(\theta=175\), find the value of (y), where (y) is an integer and \(0 \leq y<60\).
The diagram below shows a river with two bridges at \(\mathrm{A}\) and \(\mathrm{B}\) that are \(2 \mathrm{~km}\) apart. The water flows from west to east at a constant speed.

A man rowed a boat upstream. He dropped his water bottle at \(\mathrm{A}\) but he only noticed it at \(\mathrm{C}\) after rowing for another 20 minutes upstream from \(\mathrm{A}\). He immediately turned back and rowed his boat downstream, and was able to pick up his water bottle at B. Assume that the man rowed his boat at a constant speed.
Find the speed of the water flowing in the river in \(\mathrm{km} / \mathrm{h}\).
Four positive integers (x, y, z) and (w) satisfy the following equations:
\([
\begin{aligned}
& x y+x+y=104 \
& y z+y+z=146 \
& z w+z+w=524
\end{aligned}
]\)
If the product \(x y z w=2^7 \times 3^2 \times 5 \times 7\), find the value of (x+y+z+w).
In the following diagram, \(\mathrm{ABC}\) is a triangle. Points \(\mathrm{E}, \mathrm{D}\) and \(\mathrm{F}\) lie on the side \(\mathrm{BC}\) and divide the side into four equal parts. \(\mathrm{M}\) is the midpoint of \(\mathrm{AB}\) and \(\mathrm{CM}\) intersects the line segments \(\mathrm{AE}, \mathrm{AD}\) and \(\mathrm{AF}\) into the ratio (x: y: z: u) where \(x \geq y \geq z \geq\) and (x, y, z) and (u) are integers. Find the least possible value of (x+y+z+u).