Singapore Mathematics Olympiad - 2022- Senior Years - Questions

Multiple Choice Questions

Problem 01:

Suppose the roots of \(\frac{x^2}{2}+m x+n=0\) are \(\frac{m}{2}\) and \(\frac{n}{3}\). Find the smallest value of \(mn\).
(A) -1080
(B) -90
(C) 0
(D) 90
(E) 1080

Problem 02:

Which of the following is true?
(A) \(\sqrt[6]{\frac{1}{333}}<\sqrt[3]{\frac{1}{18}}<\sqrt{\frac{1}{7}}\)
(B) \(\sqrt[3]{\frac{1}{18}}<\sqrt[6]{\frac{1}{333}}<\sqrt{\frac{1}{7}}\)
(C) \(\sqrt[3]{\frac{1}{18}}<\sqrt{\frac{1}{7}}<\sqrt[6]{\frac{1}{333}}\)
(D) \(\sqrt{\frac{1}{7}}<\sqrt[6]{\frac{1}{333}}<\sqrt[3]{\frac{1}{18}}\)
(E) None of the above.

Problem 03:

Suppose \(\sqrt{\left(\log {377 \times 377} 2022\right)\left(\log {377} 2022\right)}=\log _k 2022\). Find \(k\).
(A) \(\sqrt{337}\)
(B) \(337^{\sqrt{2}}\)
(C) \(337 \sqrt{2}\)
(D) \(\sqrt{337}^{\sqrt{2}}\)
(E) \(\sqrt{337 \times 2}\)

Problem 04:

Suppose \(y=\cos ^2 x-7 \cos x+25\), where \(x\) is any real number. Find the range of \(y\).
(A) \(17 \leq y \leq 33\)
(B) \(18 \leq y \leq 33\)
(C) \(19 \leq y \leq 33\)
(D) \(20 \leq y \leq 33\)
(E) None of the above

Problem 05:

Suppose \(\sin \left(180^{\circ}+x\right)=-\frac{7}{9}\), where \(450^{\circ}<x<540^{\circ}\). Find \(\sin (2 x)\).
(A) \(\frac{49}{81} \sqrt{2}\)
(B) \(\frac{56}{81} \sqrt{2}\)
(C) \(-\frac{56}{81}\)
(D) \(-\frac{49}{81} \sqrt{2}\)
(E) \(-\frac{56}{81} \sqrt{2}\)

Short Questions

Problem 06:

Find the value of
\(\left(\frac{\cos 10^{\circ}+\cos 50^{\circ}+\cos 70^{\circ}+\cos 110^{\circ}}{\cos 20^{\circ}}\right)^8\) .

Problem 07:

Suppose \(x^{20}+\frac{x^{10}}{2}-\frac{3^{2 x}}{9}+\frac{1}{16}=0\) for some positive real number \(x\). Find the value of

\(4 \cdot 3^x-12 x^{10}\).

Problem 08:

How many positive integers less than or equal to 2022 cannot be expressed as
\(\lfloor 2 x+1\rfloor+\lfloor 5 x+1\rfloor\) for some real number \(x\) ? Here, \(\lfloor x\rfloor\) denotes the greatest integer less than or equal to \(x\). For example, \(\lfloor-2.1\rfloor=-3,\lfloor 3.9\rfloor=3\).

Problem 09:

Suppose
\(y=\frac{\tan ^2 x-\tan x+\sqrt{33}}{\tan ^2 x+\tan x+1}\),
where \(-90^{\circ}<x<90^{\circ}\). Find the maximum possible value of \(\sqrt{33}(y-5)\).

Problem 10:

In the figure below, \(P Q R S\) is a square inscribed in a circle. Let \(W\) be a point on the arc \(P Q\) such that \(W S=\sqrt{20}\). Find \((W P+W R)^2\).

Problem 11:

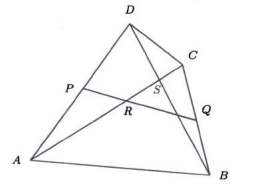
The figure below shows a quadrilateral \(A B C D\) such that \(A C=B D\) and \(P\) and \(Q\) are the midpoints of the sides \(A D\) and \(B C\) respectively. The lines \(P Q\) and \(A C\) meet at \(R\) and the lines \(B D\) and \(A C\) meet at (S). If \(\angle P R C=130^{\circ}\), find the angle \(\angle D S C\) in \({ }^{\circ})\).

Problem 12:

How many distinct terms are there if \(\left(x^2+y^2\right)^{11}\left(x^{11}+y^{11}\right)^9\) is algebraically expanded and simplified?

Problem 13:

If \(\sqrt{x^2+7 x-4}+\sqrt{x^2-x+4}=x-1\), find the value of \(3 x^2+14 x\).

Problem 14:

Let \(k=-1+\sqrt{2022^{1 / 5}-1}\), and let \(f(x)=\left(k^2+2 k+2\right)^{10 x}\). Find the value of \(\log _{2022} f(2022)\).

Problem 15:

Find the smallest odd integer \(N\), where \(N>2022\), such that when \(1808,2022\) and \(N\) are each divided by a positive integer \(p\), where \(p>1\), they all leave the same remainder.

Problem 16:

If \(\frac{12}{x}+\frac{48}{y}=1\), where \(x\) and \(y\) are positive real numbers, find the smallest possible value of \(x+y\).

Problem 17:

Find the largest value of \(40 x+60 y\) if \(x-y \leq 2,5 x+y \geq 5\) and \(5 x+3 y \leq 15\).

Problem 18:

Suppose
\(\cos x-\cos y =\frac{1}{2}\),
\(\sin x-\sin y =-\frac{1}{3}\)

If \(\sin (x+y)=\frac{m}{n})\), where \(\frac{m}{n}\) is expressed as a fraction in its lowest terms, find the value of \(m+n\).

Problem 19:

For some positive integer \(n\), the number \(n^3-3 n^2+3 n\) has a units digit of \(6\) . Find the product of the last two digits of the number \(7(n-1)^{12}+1\).

Problem 20:

Find the largest positive integer \(n\) for which \(\frac{20 n+2020}{3 n-6}\) is a positive integer.

Problem 21:

In the \(x y\)-coordinate system, there are two circles passing through the point \(11,3 \sqrt{3}\), and each of these circles is tangent to both the \(x\)-axis and the line \(y=\sqrt{3} x\). Let \(S\) be the sum of the radii of the two circles. Find \(\sqrt{3} S\).

Problem 22:

Let \(P\) and \(Q\) be the points \(20(\sqrt{5}-1), 0\) and \(0,10(\sqrt{5}-1)\) on the \(x y\)-plane. Let \(R\) be the point \(a, b\). If \(\angle P R Q\) is a right angle, find the maximum possible value of \(b\).

Problem 23:

How many positive integers \(n\) do not satisfy the inequality \(n^{\frac{1}{3} \log _{20} n}>\sqrt{n}\) ?

Problem 24:

Let \(f(x)\) be a function such that \(3 f\left(x^2\right)+f(13-4 x)=3 x^2-4 x+293\)
for all real number \(x\). Find the value of \(f(1)\).

Problem 25:

Find the largest positive integer \(M\) such that \(\cos ^2 x-\sin ^2 x+\sin x=\frac{M}{888}\) has a real solution.