Which of the five numbers, \(30^2, 10^3, 5^4, 4^5\) or \(3^6\), is the largest?
(A) \(30^2\)
(B) \(10^3\)
(C) \(5^4\)
(D) \(4^5\)
(E) \(3^6\)
Adele has a fruit basket containing one apple, two bananas and three oranges, while Betty has a fruit basket containing two apples and three oranges. Assuming that Adele and Betty each randomly picked a fruit from her own basket, what is the probability that together they picked an apple and an orange?
(A) \(\frac{1}{10}\)
(B) \(\frac{3}{10}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{6}{11}\)
(E) None of the above
The following diagram shows a system of balances hanging from the ceiling with three types of weights. The balances tip down to the heavier side. If we use \(\square<\Delta\) to represent \(\square\) is lighter than \(\Delta\), which of the following is true?
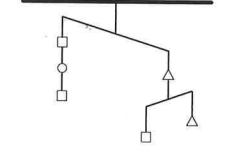
(A) \(\circ< \square<\Delta\)
(B) \(\circ<\Delta< \square\)
(C) \(\Delta< \square <\circ \)
(D) \(\Delta<\circ<\square\)
(E) Impossible to tell
A shop sells two types of buns, with either cream or jam filling, which are indistinguishable until someone bites into the buns. Four mathematicians visited the shop and ordered (not necessarily in that sequence): three cream buns, two cream buns and one jam bun, one cream and two jam buns, and three jam buns. Each knew precisely what the others had ordered. Unfortunately, the shop owner mixed up the orders and gave each mathematician the wrong order!
The mathematicians started eating, all still unaware of the mixup, until the shop owner ran over to inform them of the mistake. Mathematician A said: "I ate two buns and both had cream filling. So, if my order was wrong, I now know what type my third bun is." Mathematician B then said: "I only ate one bun and it had cream filling. Based on what A said and since I remember A's order, I now know what type my other two buns are." Finally, Mathematician C said: "I have not started eating but I must have received three jam buns." Which of the following statements about Mathematician D is correct?
(A) D ordered two cream and one jam but received three jam buns.
(B) D ordered one cream and two jam but received two cream and one jam buns.
(C) D ordered three cream but received one cream and two jam buns.
(D) D ordered three jam but received three cream buns.
(E) None of the above
If (n) can take the value of any positive integer, how many distinct values can the expression
\([
\left\lfloor\frac{n}{4}\right\rfloor-\left\lfloor\frac{n}{7}\right\rfloor-\left\lfloor\frac{n}{14}\right\rfloor-\left\lfloor\frac{n}{28}\right\rfloor
]\)
take?
(A) 1
(B) 2
(C) 3
(D) 4
(E) infinitely many
Let (n) be a positive integer. If the lowest common multiple of (n) and 12 is 60 , and the highest common factor of (n) and 36 is 4 , what is the value of (n) ?
The digits (1,2,3,4,5) and 6 are arranged to form two positive integers with each digit appearing exactly once. How many ways can this be done if the sum of the two integers is 570 ?
Consider the following product of two mixed fractions
\(m\frac{6}{7} \times n \frac{1}{3}=23\),
where (m) and (n) are positive integers. What is the value of (m+n) ?
What are the last four digits of the sum
\(222+2022+20022+\cdots+2 \underbrace{0000000000}_{\text {ten } 0 s} 22\) ?
Give your answer as a 4-digit number.
If (a) and (b) are distinct solutions to the equation
\(x^2+10 x+20=0\),
what is the value of \(a^4+b^4\) ?
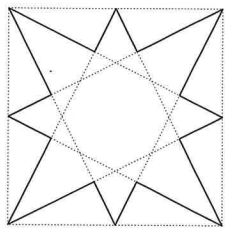
The following diagram shows a star that is cut out from a square with sides of length 30 . What is the area enclosed by the star?
If (x) is a real number, how many solutions are there to the equation
\((3 x+2)^{x+5}=1 \text { ? }\)
In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If \(\mathrm{W}\) represents 5 , what number does TROOP represent?

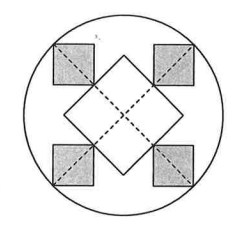
In the following diagram, a white square and four grey squares of equal size are drawn in a circle such that both dashed lines form diameters of the circle. If the diameter has length 60 , find the smallest possible value for the total area of the five squares.
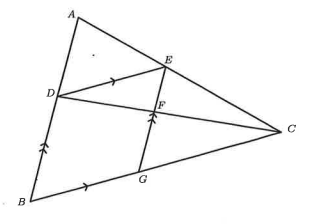
In the following diagram, (A B C) is a triangle and (D) lies on (A B) such that the ratio of \(|A D|:|D B|=3: 4\). Points (E) and (G) lie on (A C) and (B C) respectively such that (D B G E) is a parallelogram and (F) is the intersection of (D C) and (G E). If the ratio of the area of \(\triangle E D F\) to the area of (\triangle A B C) is (m: n), where the highest common factor of (m) and (n) is 1 , what is the value of \(m+n\) ?
Eggs in a certain supermarket are sold only in trays containing exactly 10,12 or 30 eggs per tray. It is thus impossible to buy exactly 14 eggs or any odd number of eggs. However, it is possible to buy exactly 78 eggs using four trays of 12 and one tray of 30 . What is the largest even number of eggs that is impossible to be bought from this supermarket?
How many integers (n) are there in \({1,2, \ldots, 2022}\) such that at least one of the digits of \(n\) is ' 2 '?
What is the smallest (k) such that every subset of \({1,2, \ldots, 99}\) with exactly \(k\) integers contains at least two distinct integers (x) and (y), such that \(|x-y| \leqslant 2\) ?
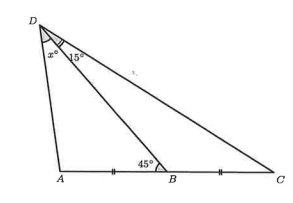
In the following diagram, (A C D) is a triangle such that \(|A B|=|B C|, \angle A B D=45^{\circ}) and (\angle B D C=15^{\circ}\). If \(\angle A D B=x^{\circ}\), what is the value of \(x\) ?
What is the area of a triangle with side lengths
\(\sqrt{6^2+7^2}, \sqrt{12^2+7^2} \text { and } \sqrt{6^2+14^2} \text { ? }\)
If \(x=\sqrt[3]{4}+\sqrt[3]{2}+1)\), what is the value of
\(2022+\frac{3}{x}+\frac{3}{x^2}+\frac{1}{x^3} ?\)
If we have
\(\frac{\sqrt{15}+\sqrt{35}+\sqrt{21}+5}{\sqrt{3}+2 \sqrt{5}+\sqrt{7}}=\frac{a \sqrt{7}+b \sqrt{5}+c \sqrt{3}}{2}\)
for some integers (a, b, c). What is the value of (a+b+c) ?
How many integers (n) are there in \({1,2, \ldots, 2022}\) such that \(\lfloor\sqrt[3]{n}\rfloor\) is a factor of \(n\) ?
If (x) and (y) can take any real values, what is the smallest possible value of the expression
\(2 x^2+4 x y+5 y^2+4 x+10 y+13 ?\)
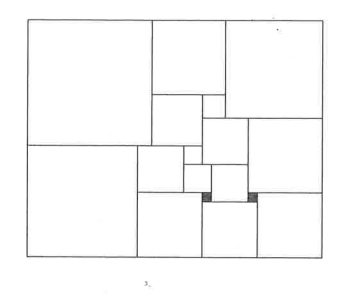
The following diagram shows a rectangle that is partitioned into 17 squares. If the two smallest squares, shaded in grey, have sides of length 2 , what is the area of the rectangle?