Let \(a\) and \(b\) be real numbers satisfying \(a<0<b\). Which of the following is not true?
(A)\(a^2 b<0\)
(B) \(a b^2<0\) (C) \(\frac{a}{b}>0\)
(D) \(b-a>0\)
(E) \(|a-b|>0\)
The following diagram shows a system of balances hanging from the ceiling with three types of weights. The balances tip down to the heavier side. If we use \(\square<\triangle\) to represent is lighter than \(\triangle\), which of the following is true?
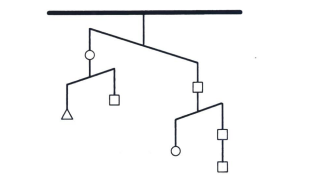
(A) \(\square<\circ<\triangle\)
(B) \(\square<\triangle<\circ\)
(C) \(\triangle<\square<\circ\)
(D) \(\triangle<\circ<\square\)
(E) \(\circ<\square<\triangle\)
Let \(x=2^{20} \cdot 3^5, y=2^5 \cdot 5^{10}\) and \(z=7^{10}\). Which of the following is true?
(A) \(x>y>z\)
(B) \(x>z>y\)
(C) \(y>z>x\)
(D) \(y>x>z\)
(E) \(z>x>y\)
In the diagram, six circles are tangent to each other. If the radius of the largest circle is \(1\) and the radii of the four medium sized circles are equal, what is the radius of the smallest circle?
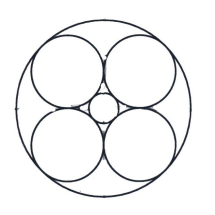
(A) \(\sqrt{2}-1\)
(B) \(3-2 \sqrt{2}\)
(C) \(2-\sqrt{2}\)
(D) \(6-4 \sqrt{2}\)
(E) None of the above
Which of the following is closest to the value of
\[\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+\cdots+\frac{1}{\sqrt{2021}+\sqrt{2020}}\]
(A) \(10\)
(B) \(20\)
(C) \(30\)
(D) \(40\)
(E) \(50\)
Let \(x\) be a positive integer. Suppose that the lowest common multiple of \(x\) and \(14\) is \(42\) and the lowest common multiple of \(x\) and \(33\) is \(66\) . What is the value of \(x\) ?
What are the last four digits of the sum
\(1+22+333+4444+\cdots+\underbrace{999999999}_{\text {nine } 9 \mathrm{~s}} \text { ? A205 }\). Give your answer as a 4-digit number.
How many distinct triples of positive integers \((a, b, c)\) satisfy \(1 \leqslant a \leqslant b \leqslant c\) and
\(\frac{1}{a_3}+\frac{1}{b_3}+\frac{1}{c_3}=1 \) ?
Given five consecutive positive integers, if the product of the largest and the smallest integer is \(2021\) , what is the sum of the five integers?
The numbers from \(1\) to \(2021\) are concatenated from left to right and the result is read as an integer \(12345678910111213 \cdots 201920202021\) .What is the remainder when this number is divided by \(6 \)?
In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If \(S\) represents \(6 \)and \(E\) represents \(8\),-what number does SIX represent?
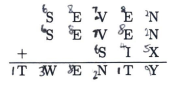
What is the value of
\(\sqrt{(219)(220)(221)(222)+1} = ?\)
Let \(A, B, \ldots, I\) be unknowns satisfying
\(A+B+C=1\),
\( B+C+D=2\),
\(C+D+E=3\),
\( D+E+F=4\),
\(E+F+G=5\),
\( F+G+H=6\),
\(G+H+I=7\) .
What is the value of \(A+E+I\) ?
If \(x\) is a 3-digit number, we define \(M(x)\) and \(m(x)\) respectively as the largest and smallest positive number that can be formed by rearranging the three digits of (x). For example, if \(x=123\), then \(M(123)=321\) and \(m(123)=123\). If \(y=898\), then \(M(898)=988\) and \(m(898)=889\).
Given that \(z\) is a 3-digit number that satisfies \(z=M(z)-m(z)\), what is the value of \(z\) ?
How many integers \(k\) are there such that the quadratic equation \(k x^2+20 x+20-k=0\) has only integer solutions?
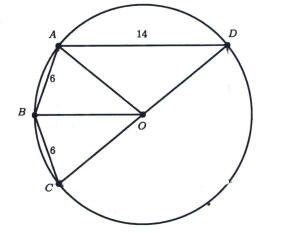
In the following diagram, \(A B C D\) is a quadrilateral inscribed in a circle with center \(O\). If \(|A B|=|B C|=6,|A D|=14\) and \(C D\) is a diameter, what is the length of \(|C D|\) ?
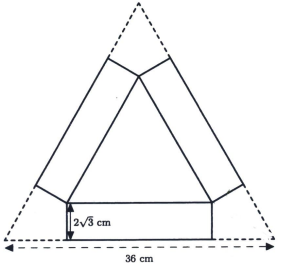
The diagram below shows a piece of cardboard in the shape of an equilateral triangle with side length \(36 \mathrm{~cm}\). Six perpendicular cuts of length \(2 \sqrt{3} \mathrm{~cm}\) are made to remove the corners in order to fold the cardboard into a tray whose base is an equilateral triangle and height is \(2 \sqrt{3} \mathrm{~cm}\). What is the volume of the tray in \(\mathrm{cm}^3\) ?
What is the value of \(\lfloor\sqrt{45+\sqrt{2021}}-\sqrt{45-\sqrt{2021}}\rfloor\) ?
Let \(x\) be the positive real number that satisfies \(\sqrt{x^2-4 x+5}+\sqrt{x^2+4 x+5}=3 x \).
What is the value of \(\left\lfloor 10^4 x^2\right\rfloor\) ?
What is the number of positive integers \(c\) such that the equation \(x^2-2021 x+100 c=0\) has real roots?
In chess, two queens are said to be attacking each other if they are positioned in the same row, column or diagonal on a chessboard. How many ways are there to place two identical queens in a \(4 \times 4\) chessboard such that they do not attack each other?
\(\frac{1}{2} \times \frac{1}{4} \times 401 \times 403 x \times 801=\)
Let \(A=\frac{3}{2} \times \frac{5}{4} \times \frac{7}{6} \times \cdots \times \frac{801}{800}\). What is the value of \(\left\lfloor\frac{A}{10}\right\rfloor\) ?
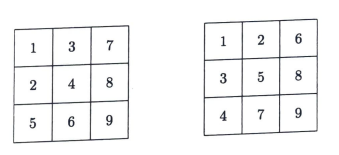
A \(3 \times 3\) grid is filled with the integers \(1\) to \(9\) . An arrangement is nicely ordered if the integers in each horizontal row is increasing from left to right and the integers in each vertical column is increasing from top to bottom. Two examples of nicely ordered arrangements are given in the diagram below. What is the total number of distinct nicely ordered arrangements?
A class has exactly \(50\) students and it is known that \(40\) students scored \(A\) in English, \(45\) scored \(A\) in Mathematics and \(42\) scored \(A\) in Science. What is the minimum number students who scored \(A\) in all three subjects?
Suppose a positive integer \(x\) satisfies the following equation
\(\sqrt[5]{x+76638}-\sqrt[5]{x-76637}=5 \).
What is the value of \(x\) ?