Let \(b\) be a positive integer. If the minimum possible value of the quadratic function \(5 x^2+b x+506\) is \(6\) , find the value of \(b\).
(A) 90
(B) 100
(C) 110
(D) 120
(E) 130
Which of the following is equal to \(\sqrt{5+\sqrt{3}}+\sqrt{5-\sqrt{3}}\) ?
(A) \(\sqrt{10-\sqrt{22}}\)
(B) \(\sqrt{10+\sqrt{22}}\)
(C) \(\sqrt{10-2 \sqrt{22}}\)
(D) \(\sqrt{10+2 \sqrt{22}}\)
(E) None of the above
Simplify
\(\log 8 5 \cdot\left(\log _5 3+\log {25} 9+\log _{125} 27\right)\) .
(A) \(\log _2 3\)
(B)\(\log _3 2\)
(C) \(\log _2 9\)
(D) \(\log _3 16\)
(E) \(\log _2 27\)
Let \(a=50^{\frac{1}{505}}, b=10^{\frac{1}{303}}\) and \(c=6^{\frac{1}{202}}\). Which of the following is true?
(A) \(a<b<c\)
(B) \(a<c<b\)
(C) \(b<a<c\)
(D) \(b<c<a\)
(E) \(c<b<a\)
Let \(p=\log _{10}(\sin x), q=(\sin x)^{10}, r=10^{\sin x}\), where \(0<x<\frac{\pi}{2}\). Which of the following is true? following is true?
(A) \(p<q<r\)
(B) \(p<r<q\)
(C) \(q<r<p\)
(D) \(q<p<r\)
(E) \(r<p<q\)
Find the minimum possible value of \(|x-10|-|x-20|+|x-30|\), where \(x\) is any real number.
Parallelogram \(A B C D\) has sides \(A B=39 \mathrm{~cm}\) and \(B C=25 \mathrm{~cm}\). Find the length of diagonal \(A C\) in \(\mathrm{cm}\) if diagonal \(B D=34 \mathrm{~cm}\).
Suppose \(\sin 45^{\circ}-x\)=\(-\frac{1}{3}\), where \(45^{\circ}<x<90^{\circ}\). Find \(6 \sin x-\sqrt{2})^2\).
If \(8 \cos x-8 \sin x=3\), find the value of \(55 \tan x+\frac{55}{\tan x}\).
Find the number of ordered pairs \(x, y\), where \(x\) and \(y\) are integers, such that
\(x^2+y^2-20 x-14 y+140<0\) .
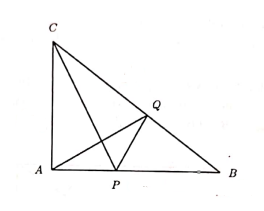
The figure below shows a right-angled triangle \(A B C\) such that \(\angle B A C=90^{\circ}, \angle A B C=\) \(30^{\circ}\) and \(A B=48 \mathrm{~cm}\). Let \(P\) be a point on side \(A B\) such that \(C P\) is the angle bisector of \(\angle A C B\) and \(Q\) be a point on side \(B C\) such that line \(A Q\) is perpendicular to line \(C P\). Determine the length of \(P Q\).
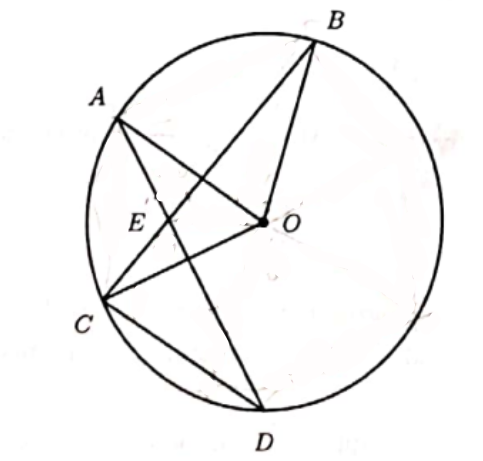
In the figure below, the point \(O\) is the center of the circle, \(A D\) and \(B C\) intersect at \(E\), and \(\angle A E B=70^{\circ}, \angle A O B=62^{\circ}\). Find the angle \(\angle O C D\left(\right.)\) in degree \(\left.{ }^{\circ}\right)\).
Find the value of \(\frac{4 \cos 43^{\circ}}{\sin 73^{\circ}}-\frac{12 \sin 43^{\circ}}{\sqrt{3} \sin 253^{\circ}}\).
If \(\frac{x^2}{5}+\frac{y^2}{7}=1\), find the largest possible value of \((x+y)^2\).
Find the coefficient of \(x^6\) in the expansion of \(\left(1+x+2 x^2\right)^7\).
Suppose \(3 x-y)^2+\sqrt{x+38+14 \sqrt{x-11}}+|z+x-y|=7\). Find the value of \(|x+y+z|\).
Suppose there are real numbers (x, y, z) satisfying the following equations: \(x+y+z=60, x y-z^2=900\) Find the maximum possible value of \(|z|\).
Find the sum \(\sum_{k=1}^{16} \log _2\left(\sqrt{\sin ^2 \frac{k \pi}{8}+1}-\sin \frac{k \pi}{8}\right)\)
Let \(a, b\) be positive real numbers, where \(a>b\). Suppose there exists a real number (x) such that \(\left(\log _2 a x\right)\left(\log _2 b x\right)+25=0\). Find the minimum possible value of \(\frac{a}{b}\).
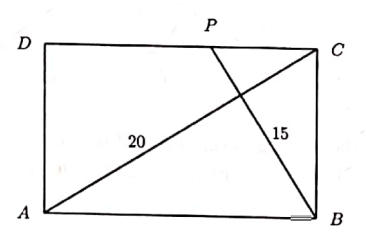
The figure below shows a rectangle (A B C D) such that the diagonal \(A C=20 \mathrm{~cm}\). Let (P) be a point on side \(C D\) such that \(B P\) is perpendicular to diagonal \(A C\). Find the area of rectangle \(A B C D\) \(in (\mathrm{cm}^2) \) if \(B P=15 \mathrm{~cm}\).
Find the smallest positive integer that is greater than the following expression:
(\(\sqrt{7}+\sqrt{5})^4\).
Find the number of non-congruent right-angled triangles such that the length of all their sides are integers and that the hypotenuse has a length of \(65 \mathrm{~cm}\).
There are 6 couples, each comprising a husband and a wife. Find the number of ways to divide the 6 couples into 3 teams such that each team has exactly 4 members, and that the husband and the wife from the same couple are in different teams.
The digit sum of a number, say 987 , is the sum of its digits, \(9+8+7=24\). Let (A) be the digit sum of \(2020^{2021}\), and let (B) be the digit sum of (A). Find the digit sum of (B).
\(40=2 \times 2 \times 2 \times 5\) is a positive divisor of 1440 that is a product of 4 prime numbers. \(48=2 \times 2 \times 2 \times 2 \times 3\) is a positive divisor of 1440 that is a product of 5 prime numbers. Find the sum of all the positive divisors of 1440 that are products of an odd number of prime numbers.