Which of the five numbers \(2^{30}, 3^{19}, 4^{14}, 6^{12}, 9^{10}\)
has the largest value?
(A) \(2^{30}\)
(B) \(3^{19}\)
(C) \(4^{14}\)
(D) \(6^{12}\)
(E) \(9^{10}\)
In a strange island. there are only two types of inhabitants: truth-tellers who only tell the truth and liars who only tell lies. One day, you meet two such inhabitants \(A\) and \(B\). \(A\) said "Exactly one of us is a truth teller." \(B\) kept silent. Which of the following must be true?
(A) Both \(A\) and \(B\) are truth-tellers
(B) Both \(A\) and \(B\) are liars
(C) \(A\) is a truth-teller and \(B\) is a liar
(D) \(A\) is a liar and \(B\) is a truth-teller
(E) Not enough information to decide
If \(x-\frac{1}{x}=3\), what is the value of \(\frac{21}{2}-\frac{3}{6} x^2+\frac{3}{2} x\) ?
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
Let \(x, y\) and \(z\) be positive integers satisfying
\(x^2+y^2+z^2=2(x y+1) \quad \text { and } \quad x+y+z=2022\) .
If \(x_1\) and \(x_2\) are two distinct solutions for \(x\), what is the value of \(x_1+x_2\) ?
(A) 2019
(B) 2020
(C) 2021
(D) 2022
(E) 2023
In a quadrilateral \(A B C D\), the diagonals \(A C\) and \(B D\) intersect at the point \(O\). Suppose that \(\angle B A D+\angle A C B=180^{\circ},|B C|=3,|A D|=4,|A C|=5\) and \(|A B|=6\). What is the value of \(\frac{|O D|}{|O B|}\) ?
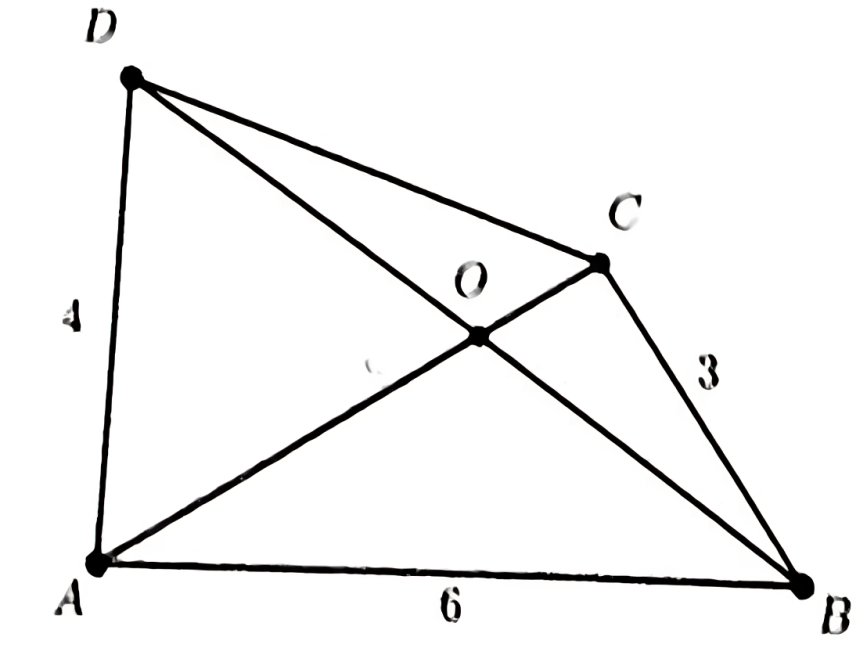
(A) \(\frac{2}{3}\)
(B) \(\frac{8}{9}\)
(C) \(\frac{9}{10}\)
(D) \(\frac{10}{9}\)
(E) \(\frac{9}{8}\)
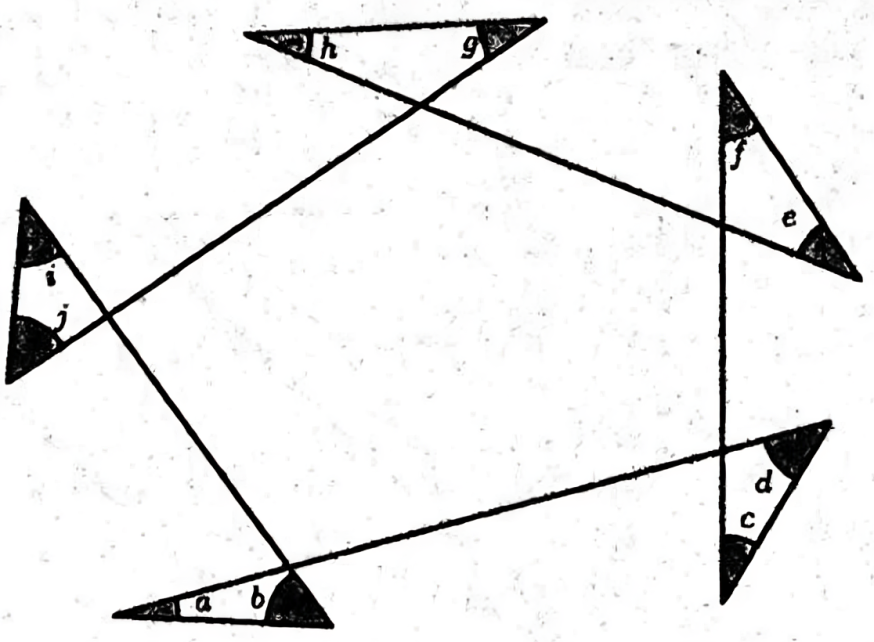
In the following diagram, all lines are straight. What is the value \(\left(\right.\) in \(\left.^{\circ}\right)\) of
\[
\angle a+\angle b+\angle c+\angle d+\angle e+\angle f+\angle g+\angle h+\angle i+\angle j ?
\]
Let \(x\) be a positive integer. Suppose that the highest common factor of \(x\) and 80 is 40 and the highest common factor of \(x\) and 252 is 12 . What is the minimum value of \(x\) ?
Suppose that \(m\) and \(n\) are positive integers where \(\frac{100 m}{n}\) is a perfect cube greater than 1 . What is the minimum value of \(m+n\) ?
What is the largest possible two-digit positive integer that is 18 more than the product of its two digits?
A teacher spent \(\$ 77\) to purchase 25 gifts for her class. There were three different types with respective unit prices \(\$ 2, \$ 4\), and \(\$ 5\). If she bought more than three gifts of each type, how many of the \(\$ 2\) gifts did she buy?
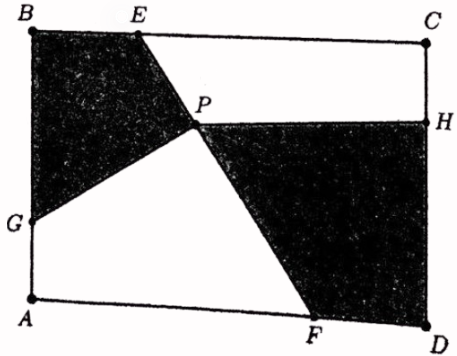
In the following diagram, \(A B C D\) is a rectangle with \(|A B|=4\) and \(|B C|=6\). Points \(E\) and \(F\) lie on the sides \(B C\) and \(A D\) respectively such that \(|B E|=|F D|=2\). Points \(G\) and \(H\) lie on the sides \(A B\) and \(C D\) respectively such that \(|A G|=|C H|=1\). Suppose \(P\) lies on \(E F\), such that the quadrilateral \(B G P E\) has area 5 . What is the area of the quadrilateral \(F D H P ?\)
Two boxes \(A\) and \(B\) contain an equal number of toys. If one of the toys, with value \(\$ 6\), is transferred from \(A\) to \(B\), the average value of the toys in box \(A\) will decrease by \(\$ 1\), while the average value of the toys in box \(B\) will increase by \(\$ 1\). Suppose every toy has a positive value, what is the total value (in \(\$\) of the toys in the two boxes?
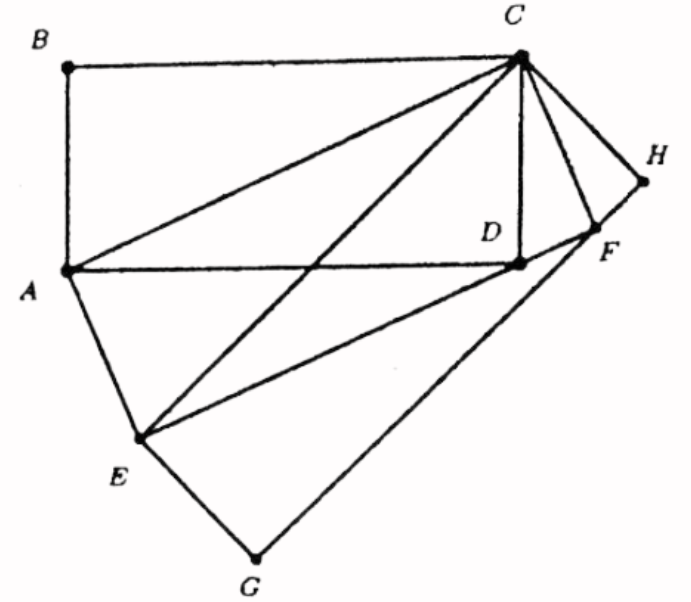
In the following diagram, \(A B C D, A C F E\) and \(E C H G\) are all rectangles. If \(|A B|=6\) and \(|B C|=8\), what is area of the rectangle \(E C H G\) ?
What is the value of \(\sqrt{199^2+800}\) ?
A student wrote the following 99 numbers on the board:
\[1,-2,3,-4,5,-6, \ldots,-98,99\]
She arbitrarily picked two of these numbers, say \(a\) and \(b\), and replaced them by the sum \(a+b\). For example, if she had picked 37 and -24 , she would erase those two numbers and add the number 13 to the board. Suppose that she repeated the process, and after 98 replacements, there was one number left on the board. What is the largest possible value of this number?
If the equation \(\frac{x-1}{x-5}=\frac{m}{10-2 x}\) has no solutions in \(x\), what is the value of \(|m| ?\)
If
\[
S=\frac{1+3+5+\cdots+2019}{2+4+6+\cdots+2020}
\]
what is the value of \(1011 S ?\)
A five-digit positive integer \(x\) has the following properties:
(i) \(x\) has distinct digits which are from \({1,2,3,4,5}\);
(ii) \(x>23456\).
How many possible values can \(x\) take?
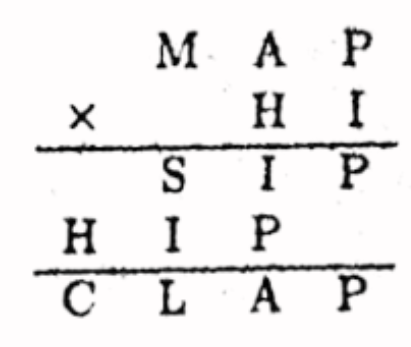
In the figure below, each distinct letter represents a unique digit such that the arithmetic holds. What digit does the letter \(\mathrm{L}\) represent?
If (x) is a nonnegative real number, find the minimum value of
\[
\sqrt{x^2+4}+\sqrt{x^2-24 x+153} .
\]
A positive integer is said to be "twelvish" if the sum of digits in its decimal representation is equal to 12. For example, the first four twelvish integers are 39,48,57 and 66 . What is the total number of twelvish integers between 1 and 999 ?
Two secondary one and \(m\) secondary two students took part in a round-robin chess tournament. In other words, each student played with every other student exactly once. For each match, the winner receives 3 points and the loser 0 points. If a match ends in a draw, both contestants receive 1 point each. If the total number of points received by all students was 130 , and the number of matches that ended in a draw was less than half of the total number of matches played, what is the value of \(m\) ?
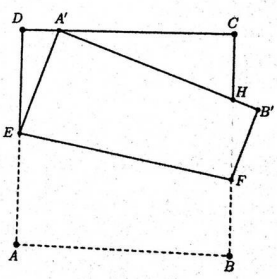
\(A B C D\) is a square sheet of paper with sides of length 6 . The paper is folded along a crease line \(E F\) so that points \(A\) and \(B\) now lie on \(A^{\prime}\) and \(B^{\prime}\) respectively as indicated in the diagram. If \(H\) is the intersection of \(A^{\prime} B^{\prime}\) and \(B C\), what is the perimeter of the triangle \(A^{\prime} C H\)?
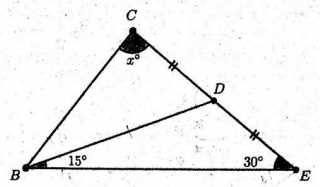
In the following diagram, \(\angle B E D=30^{\circ}\) and \(\angle D B E=15^{\circ}\). If \(|C D|=|D E|\), what is the value of \(x\) ?
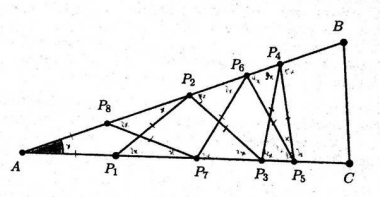
In the following diagram, \(P_1, P_2, \cdots, P_8\) are points on \(\triangle A B C\) such that
\(\left|A P_1\right|=\left|A P_8\right|=\left|P_i P_{i+1}\right|, \text { for all } i=1,2, \cdots, 7 \).
What is the value in \({ }^{\circ}\) of \(\angle B A C\) ?