How many non-congruent triangles with integer side lengths have perimeter 7 ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
The following diagram shows two semicircles whose diameters lie on the same line. (A B) is a chord of the larger semicircle that is tangent to the smaller semicircle at the point \(\mathrm{C}\) and is parallel to the diameter \(\mathrm{DE}\) of the larger semicircle. If \(|\mathrm{AB}|=16 \mathrm{~cm}\), what is the area of the shaded region in \(\mathrm{cm}^2\) ?
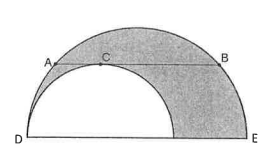
(A) \(8 \pi\)
(B) \(16 \pi\)
(C) \(32 \pi\)
(D) \(48 \pi\)
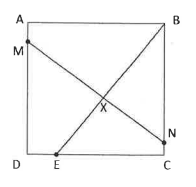
In the following diagram, \(\mathrm{ABCD}\) is a square of side \(16 \mathrm{~cm}\). \(\mathrm{E}\) lies on \(\mathrm{CD}\) such that \(|\mathrm{DE}|=) (4 \mathrm{~cm} . \mathrm{M}) and (\mathrm{N}\) lie on \(\mathrm{AD}\) and \(\mathrm{BC}\) respectively such that \(\mathrm{MN}\) is perpendicular to \(\mathrm{BE} . \mathrm{X}\) is the intersection of \(\mathrm{MN}\) and \(\mathrm{BE}). If (|\mathrm{MX}|=11 \mathrm{~cm}\) and \(|\mathrm{BN}|=x \mathrm{~cm}\), what is the value of (x) ?
The sum of all the interior angles except one of a convex polygon is \(2023^{\circ}\). What is the number of sides of this polygon? (A polygon is convex if every interior angle is between \(0^{\circ}\) and \(180^{\circ}).\)
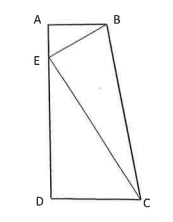
In the following diagram, (A B) is parallel to \(\mathrm{DC},|\mathrm{AB}|=6 \mathrm{~cm},|\mathrm{AD}|=17 \mathrm{~cm},|\mathrm{DC}|=10 \mathrm{~cm}\) and angle \(\mathrm{DAB}=90^{\circ}\). \(\mathrm{E}\) lies on \(\mathrm{AD}\) such that \(\mathrm{BE}\) is perpendicular to \(\mathrm{EC}\). If the area of triangle \(\mathrm{BEC}=k \mathrm{~cm}^2\), what is the largest possible value of (k) ?
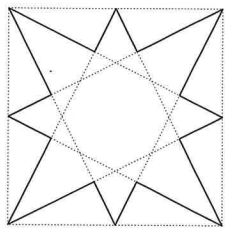
The following diagram shows a star that is cut out from a square with sides of length 30 . What is the area enclosed by the star?
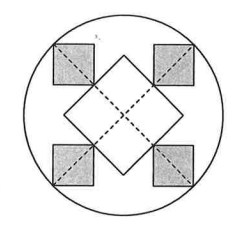
In the following diagram, a white square and four grey squares of equal size are drawn in a circle such that both dashed lines form diameters of the circle. If the diameter has length 60 , find the smallest possible value for the total area of the five squares.
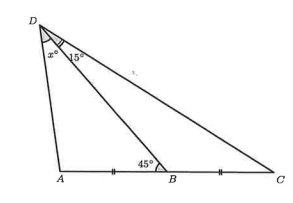
In the following diagram, (A C D) is a triangle such that \(|A B|=|B C|, \angle A B D=45^{\circ}) and (\angle B D C=15^{\circ}\). If \(\angle A D B=x^{\circ}\), what is the value of \(x\) ?
What is the area of a triangle with side lengths
\(\sqrt{6^2+7^2}, \sqrt{12^2+7^2} \text { and } \sqrt{6^2+14^2} \text { ? }\)
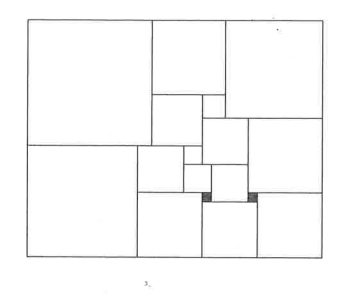
The following diagram shows a rectangle that is partitioned into 17 squares. If the two smallest squares, shaded in grey, have sides of length 2 , what is the area of the rectangle?
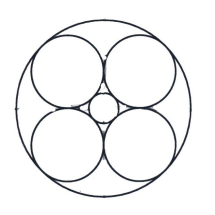
In the diagram, six circles are tangent to each other. If the radius of the largest circle is 1 and the radii of the four medium sized circles are equal, what is the radius of the smallest circle?
(A) \(\sqrt{2}-1\)
(B) \(3-2 \sqrt{2}\)
(C) \(2-\sqrt{2}\)
(D) \(6-4 \sqrt{2}\)
(E) None of the above
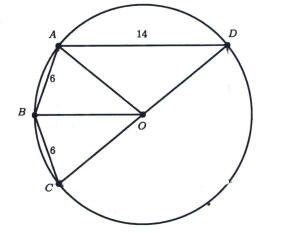
In the following diagram, \(A B C D\) is a quadrilateral inscribed in a circle with center \(O\). If \(|A B|=|B C|=6,|A D|=14\) and \(C D\) is a diameter, what is the length of \(|C D|\) ?
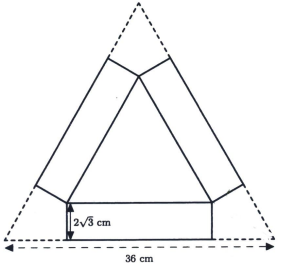
The diagram below shows a piece of cardboard in the shape of an equilateral triangle with side length \(36 \mathrm{~cm}\). Six perpendicular cuts of length \(2 \sqrt{3} \mathrm{~cm}\) are made to remove the corners in order to fold the cardboard into a tray whose base is an equilateral triangle and height is \(2 \sqrt{3} \mathrm{~cm}\). What is the volume of the tray in \(\mathrm{cm}^3\) ?
Let (A B C) be a triangle where (D) is the midpoint of (B C) and (E) lies on (A C) such that (A E: E C=3: 1). Let (F) be the intersection of (A D) and (B E). If the area of (A B C) is 280 , what is the area of triangle (B F D) ?
In the following diagram, (A B C D) is a rectangle where (E) and (F) are points on (B C) and (C D) respectively. The area of triangle (A E F), denoted ([A E F]), is 2037 . If
\([
[A E C F]=2[A B E]=3[A D F],
]\)
what is the area of the rectangle (A B C D) ?
In the following diagram, (A B C D) is a square of side length (64 . E) is the midpoint of (A B), (F) is the midpoint of (E C) and (G) is the midpoint of (F D). What is the area enclosed by the quadrilateral (A E F G) ?
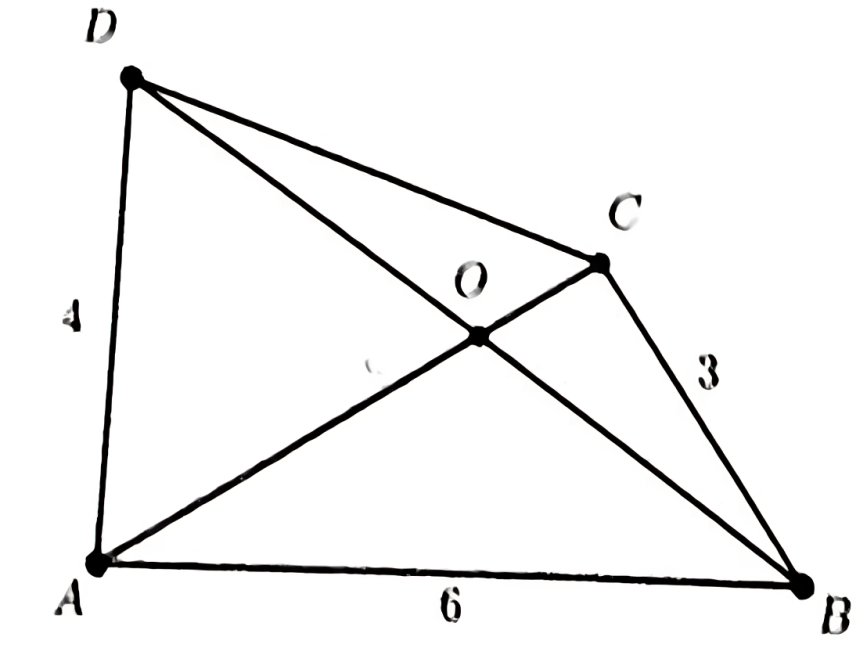
In a quadrilateral \(A B C D\), the diagonals \(A C\) and \(B D\) intersect at the point \(O\). Suppose that \(\angle B A D+\angle A C B=180^{\circ},|B C|=3,|A D|=4,|A C|=5\) and \(|A B|=6\). What is the value of \(\frac{|O D|}{|O B|}\) ?
(A) \(\frac{2}{3}\)
(B) \(\frac{8}{9}\)
(C) \(\frac{9}{10}\)
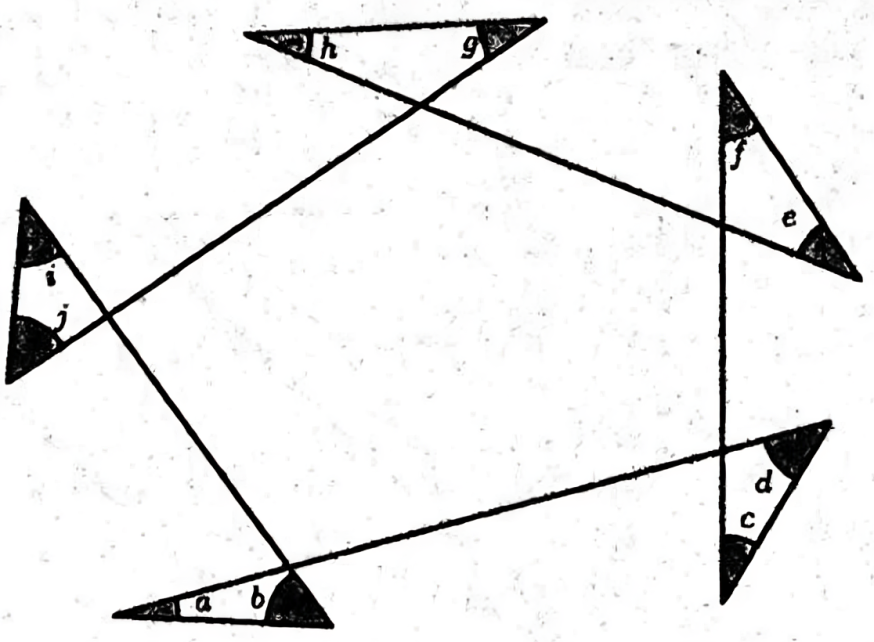
In the following diagram, all lines are straight. What is the value \(\left(\right.\) in \(\left.^{\circ}\right)\) of
\[
\angle a+\angle b+\angle c+\angle d+\angle e+\angle f+\angle g+\angle h+\angle i+\angle j ?
\]
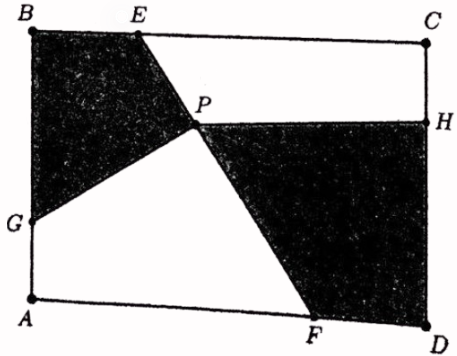
In the following diagram, \(A B C D\) is a rectangle with \(|A B|=4\) and \(|B C|=6\). Points \(E\) and \(F\) lie on the sides \(B C\) and \(A D\) respectively such that \(|B E|=|F D|=2\). Points \(G\) and \(H\) lie on the sides \(A B\) and \(C D\) respectively such that \(|A G|=|C H|=1\). Suppose \(P\) lies on \(E F\), such that the quadrilateral \(B G P E\) has area 5 . What is the area of the quadrilateral \(F D H P ?\)
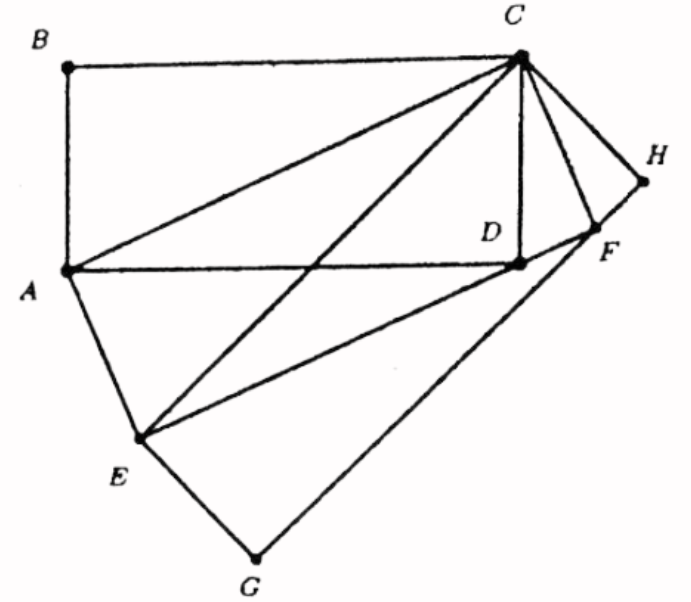
In the following diagram, \(A B C D, A C F E\) and \(E C H G\) are all rectangles. If \(|A B|=6\) and \(|B C|=8\), what is area of the rectangle \(E C H G\) ?
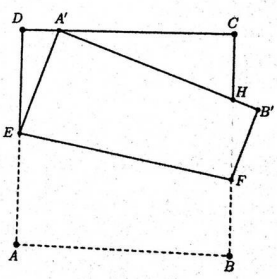
\(A B C D\) is a square sheet of paper with sides of length 6 . The paper is folded along a crease line \(E F\) so that points \(A\) and \(B\) now lie on \(A^{\prime}\) and \(B^{\prime}\) respectively as indicated in the diagram. If \(H\) is the intersection of \(A^{\prime} B^{\prime}\) and \(B C\), what is the perimeter of the triangle \(A^{\prime} C H\)?
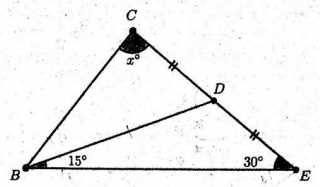
In the following diagram, \(\angle B E D=30^{\circ}\) and \(\angle D B E=15^{\circ}\). If \(|C D|=|D E|\), what is the value of \(x\) ?
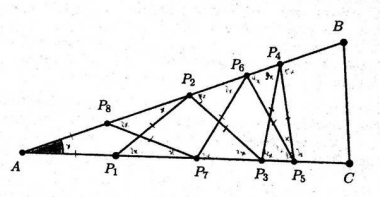
In the following diagram, \(P_1, P_2, \cdots, P_8\) are points on \(\triangle A B C\) such that
\(
\left|A P_1\right|=\left|A P_8\right|=\left|P_i P_{i+1}\right|, \text { for all } i=1,2, \cdots, 7 .
\)
What is the value \(in ({ }^{\circ}) \) of \(\angle B A C\) ?