Singapore Math Olympiad Past ears Questions- Combinatorics (Junior)
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesA shop sells two types of buns, with either cream or jam filling, which are indistinguishable until someone bites into the buns. Four mathematicians visited the shop and ordered (not necessarily in that sequence): three cream buns, two cream buns and one jam bun, one cream and two jam buns, and three jam buns. Each knew precisely what the others had ordered. Unfortunately, the shop owner mixed up the orders and gave each mathematician the wrong order!
The mathematicians started eating, all still unaware of the mixup, until the shop owner ran over to inform them of the mistake. Mathematician A said: "I ate two buns and both had cream filling. So, if my order was wrong, I now know what type my third bun is." Mathematician B then said: "I only ate one bun and it had cream filling. Based on what A said and since I remember A's order, I now know what type my other two buns are." Finally, Mathematician C said: "I have not started eating but I must have received three jam buns." Which of the following statements about Mathematician D is correct?
(A) D ordered two cream and one jam but received three jam buns.
(B) D ordered one cream and two jam but received two cream and one jam buns.
(C) D ordered three cream but received one cream and two jam buns.
(D) D ordered three jam but received three cream buns.
(E) None of the above
The digits (1,2,3,4,5) and 6 are arranged to form two positive integers with each digit appearing exactly once. How many ways can this be done if the sum of the two integers is 570 ?
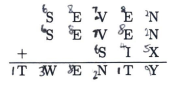
In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If \(\mathrm{W}\) represents 5 , what number does TROOP represent?

Eggs in a certain supermarket are sold only in trays containing exactly 10,12 or 30 eggs per tray. It is thus impossible to buy exactly 14 eggs or any odd number of eggs. However, it is possible to buy exactly 78 eggs using four trays of 12 and one tray of 30 . What is the largest even number of eggs that is impossible to be bought from this supermarket?
In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If \(S\) represents \(6 \)and \(E\) represents \(8\),-what number does SIX represent?
In chess, two queens are said to be attacking each other if they are positioned in the same row, column or diagonal on a chessboard. How many ways are there to place two identical queens in a (4 \times 4) chessboard such that they do not attack each other?
\(\frac{1}{2} \times \frac{1}{4} \times 401 \times 403 x \times 801=\)
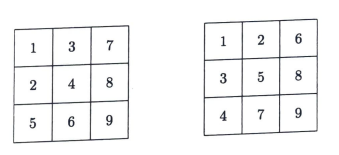
A \(3 \times 3\) grid is filled with the integers 1 to 9 . An arrangement is nicely ordered if the integers in each horizontal row is increasing from left to right and the integers in each vertical column is increasing from top to bottom. Two examples of nicely ordered arrangements are given in the diagram below. What is the total number of distinct nicely ordered arrangements?
A class has exactly 50 students and it is known that 40 students scored (A) in English, 45 scored (A) in Mathematics and 42 scored (A) in Science. What is the minimum number students who scored (A) in all three subjects?
An expensive painting was stolen and the police rounded up five suspects Alfred, Boris, Chucky, Dan and Eddie. These were the statements that were recorded.
Alfred: "Either Boris or Dan stole the painting."
Boris: "I think Dan or Eddie is the guilty party."
Chucky: "It must be Dan."
Dan: "Boris or Eddie did it!"
Eddie: "I am absolutely sure the thief is Alfred."
The police knew that only one of the five suspects stole the painting and that all five were lying. Who stole the painting?
(A) Alfred
(B) Boris
(C) Chucky
(D) Dan
(E) Eddie
In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If the letter K represents 6 , what number does SHAKE represent?
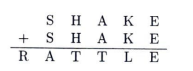
Ali and Barry went running on a standard 400 metre track. They started simultaneously at the same location on the track but ran in opposite directions. Coincidentally, after 24 minutes, they ended at the same location where they started. Ali completed 12 rounds of the track in those 24 minutes while Barry completed 10 rounds. How many times did Ali and Barry pass each other during the run? (Exclude from your answer the times that they met at the start of the of run and when they completed the run after 24 minutes.)
In a strange island. there are only two types of inhabitants: truth-tellers who only tell the truth and liars who only tell lies. One day, you meet two such inhabitants \(A\) and \(B\). \(A\) said "Exactly one of us is a truth teller." \(B\) kept silent. Which of the following must be true?
(A) Both \(A\) and \(B\) are truth-tellers
(B) Both \(A\) and \(B\) are liars
(C) \(A\) is a truth-teller and \(B\) is a liar
(D) \(A\) is a liar and \(B\) is a truth-teller
(E) Not enough information to decide
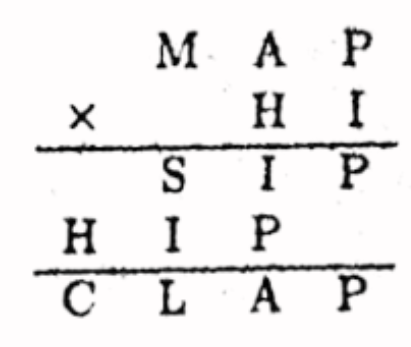
In the figure below, each distinct letter represents a unique digit such that the arithmetic holds. What digit does the letter \(\mathrm{L}\) represent?
Two secondary one and \(m\) secondary two students took part in a round-robin chess tournament. In other words, each student played with every other student exactly once. For each match, the winner receives 3 points and the loser 0 points. If a match ends in a draw, both contestants receive 1 point each. If the total number of points received by all students was 130 , and the number of matches that ended in a draw was less than half of the total number of matches played, what is the value of \(m\) ?