The value of $\frac{9999+7777+5555}{8888+6666+4444}$ is
A) 1
B) $\frac{755}{448}$
C) $\frac{7}{6}$
D) $\frac{1}{6}$
The sum of three prime numbers is 30 . How many such sets of prime numbers are there?
A) 1
B) 2
C) 3
D) 0

In the adjoining figure, lines $\ell_1, \ell_2$ are parallel lines. $A B C$ is an equilateral triangle.
$A D$ bisects $\angle E A B$.
Then $x=$ ?
A) $100^{\circ}$
B) $95^{\circ}$
C) $105^{\circ}$
D) $110^{\circ}$
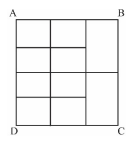
In the figure, $A B C D$ is a square. It consists of squares and rectangles of areas $1 \mathrm{~cm}^2$ and $2 \mathrm{~cm}^2$ as shown. The perimeter of the square $A B C D$ (in cm ) is
A) 17
B) 15
C) 16
D) 14
If $a * b=\frac{a+b}{a-b}$, then the value of $\frac{13 * 6}{5 * 2}$ is
A) $\frac{21}{4}$
B) $\frac{17}{3}$
C) $\frac{19}{39}$
D) $\frac{57}{49}$
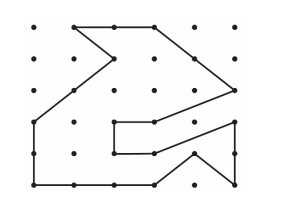
In the adjoining figure, the distance between any two adjacent dots is 1 cm . The area of the shaded region (in $\mathrm{cm}^2$ ) is
A) $\frac{31}{3}$
B) $\frac{31}{2}$
C) $\frac{33}{2}$
D) $\frac{35}{2}$
Three natural numbers $n_1, n_2, n_3$ are taken.
Let $n_{1<} n_{2<} n_3$ and $n_1+n_2+n_3=6$. The value of $n_3$ is
A) 1
B) 2
C) 3
D) 1 or 2 or 3
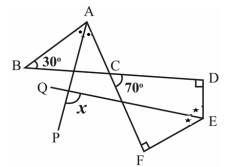
In the adjoining figure, AP and EQ are respectively the bisectors of $\angle \mathrm{BAC}$ and $\angle \mathrm{DEF}$. Then, the measure of angle $x$ is
A) $90^{\circ}$
B) $85^{\circ}$
C) $105^{\circ}$
D) $75^{\circ}$
The number of two-digit positive integers which have at least one 7 as a digit is
A) 17
B) 19
C) 9
D) 18
The fractions $\frac{1}{5}$ and $\frac{1}{3}$ are shown on the number line. In which position should $\frac{1}{4}$ be shown?
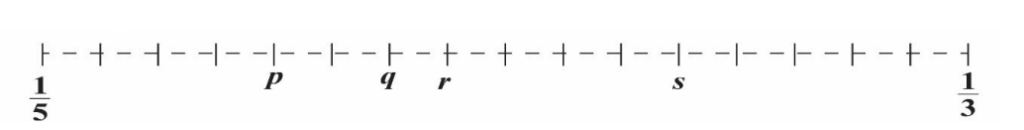
A) $p$
B) $q$
C) $r$
D) $s$
Samrud reads $\frac{1}{3}$ of a story book on the first day, $\frac{1}{2}$ of the remaining book on the second day and $\frac{\mathbf{1}}{\mathbf{4}}$ of the remaining book as on the end of the first day, on the third day and left with 23 pages unread. The number of pages of the book is
A) 138
В) 148
C) 128
D) 136
The product of four different natural numbers is 100 . What is the sum of the four numbers?
A) 20
B) 10
C) 12
D) 18
Peter starts from a point A in a playground and walks $100 m$ towards East. Then he walks 30 m towards North and then 70 m towards West and then finally 10 m North to reach the point B. The distance between A and B (in metres) is
A) 50
B) 42
C) 40
D) 30
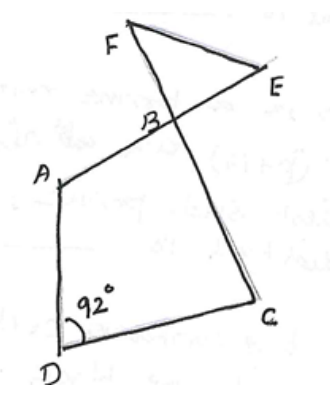
In the adjoining figure $\angle \mathrm{DAB}$ is $8^{\circ}$ more than $\angle \mathrm{ADC}$; $\angle \mathrm{BCD}$ is $8^{\circ}$ less than $\angle \mathrm{ADC}$. $\angle \mathrm{FEB}$ is half of $\angle \mathrm{FBE}$. Then the measure of $\angle \mathrm{BFE}$ is
A) $54^{\circ}$
B) $52^{\circ}$
C) $49^{\circ}$
D) $50^{\circ}$
The fraction to be added to the fraction $\frac{1}{2+\frac{1}{3+\frac{1}{1+\frac{1}{4}}}}$ to get 1 is
A) $\frac{26}{43}$
В) $\frac{18}{43}$
C) $\frac{24}{43}$
D) $\frac{23}{43}$
Some amount of money is divided among A, B and C, so that for every ₹100 A has, B has ₹ 65 and c has ₹ 40. If the share of C is ₹ 4000, the total amount of money (in ₹) is $\rule{2cm}{0.2mm}$.
ABCDE is a pentagon. The angles $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}$ are in the ratio 8:9:12:15:10. The external bisector of B and the internal bisector of C meet at P . Then the measure of $\angle \mathrm{BPC}$ is $\rule{2cm}{0.2mm}$.
The least number, when lessened (decreased) by 5 , to be divisible by 36,48 , 21 , and 28 is $\rule{2cm}{0.2mm}$.
When $10 \frac{5}{6}$ is divided by 91 , we get a fraction $\frac{a}{b}$, where $a, b$ are natural numbers with no common factors other than 1 ; then $(b-a)$ is equal to $\rule{2cm}{0.2mm}$.
Let $p$ be the smallest prime number such that the numbers $(p+6),(p+8)$, $(p+12)$ and $(p+14)$ are also prime. Then the remainder when $p^2$ is divided by 4 is $\rule{2cm}{0.2mm}$.
A bag contains certain number of black and white balls, of which $60 \%$ are black. When 9 white balls are added to the bag, the ratio of the black balls to the white balls is $4: 3$. The number of white balls in the bag at the beginning is $\rule{2cm}{0.2mm}$.

In the adjoining figure, the sum of the measures of the angles $a, b, c, d, e, f$ is $\rule{2cm}{0.2mm}$.
A basket contains apples, bananas, and oranges. The total number of apples and bananas is 88 . The total number of apples and oranges is 80 . The total number of bananas and oranges is 64 . Then the number of apples is $\rule{2cm}{0.2mm}$.
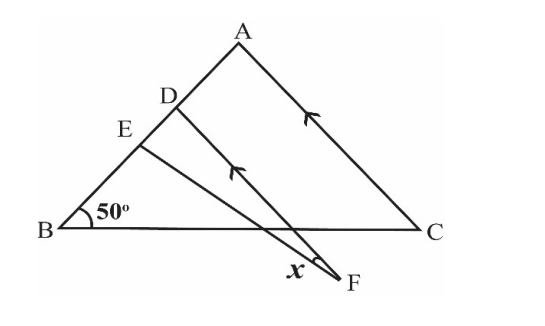
ABC is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$ EDF is an isosceles triangle in which $\mathrm{EF}=\mathrm{DE}$. FD is parallel to AC . The degree measure of marked angle $x$ is $\rule{2cm}{0.2mm}$.
The length and breadth of a rectangle are both prime numbers, and its perimeter is 40 cm . Then the maximum possible area of the rectangle (in $\mathrm{cm}^2$ ) is $\rule{2cm}{0.2mm}$.
Please give answers of these questions