This problem from American Mathematics contest (AMC 8, 2019) will help us to learn more about Menalaus Theorem. Try it out!
Competency in Focus: Menalaus Theorem

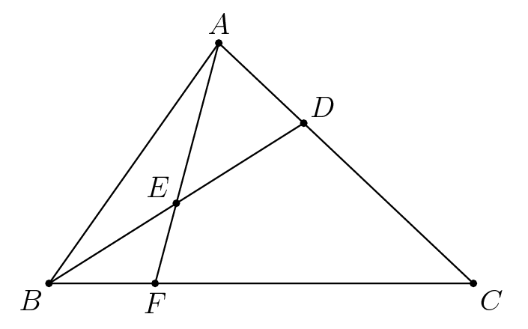
In triangle $A B C$, point $D$ divides side $\overline{A C}$ so that $A D: D C=1: 2$. Let $E$ be the midpoint of $\overline{B D}$ and let $F$ be the point of intersection of line $B C$ and line $A E$. Given that the area of $\triangle A B C$ is 360 , what is the area of $\triangle E B F$ ?
(A) 24
(B) 30
(C) 32
(D) 36
(E) 40
AMC 8, 2019 Problem 24
Menalaus's Theorem:
Given a triangle ABC, and a transversal line that crosses BC, AC, and AB at points D, E, and F respectively, with D, E, and F distinct from A, B, and C, then
$\frac{A F}{F B} \times \frac{B D}{D C} \times \frac{C E}{E A}=-1$
Challenges and Thrills in Pre College Mathematics Excursion Of Mathematics
7 out of 10