[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row _builder_version="3.25"][et_pb_column type="4_4" _builder_version="3.25" custom_padding="|||" custom_padding__hover="|||"][et_pb_accordion open_toggle_text_color="#0c71c3" _builder_version="3.22.4" toggle_font="||||||||" body_font="Raleway||||||||" text_orientation="center" custom_margin="10px||10px"][et_pb_accordion_item title="Source of the problem" open="on" _builder_version="4.0"]Israel MO 2019 Problem 3[/et_pb_accordion_item][et_pb_accordion_item title="Topic" _builder_version="4.0" open="off"]Geometry[/et_pb_accordion_item][et_pb_accordion_item title="Difficulty Level" _builder_version="4.0" open="off"]6/10[/et_pb_accordion_item][et_pb_accordion_item title="Suggested Book" _builder_version="4.0" open="off"]Challenges and Thrills of PreCollege Mathematics[/et_pb_accordion_item][/et_pb_accordion][et_pb_text _builder_version="3.27.4" text_font="Raleway|300|||||||" text_text_color="#ffffff" header_font="Raleway|300|||||||" header_text_color="#e2e2e2" background_color="#0c71c3" custom_margin="48px||48px" custom_padding="20px|20px|20px|20px" border_radii="on|5px|5px|5px|5px" box_shadow_style="preset3"]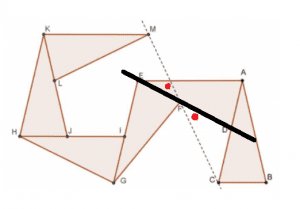
We will now proceed towards proving in this direction.[/et_pb_tab][et_pb_tab title="Hint 2" _builder_version="4.0"]Let's investigate the triangle FDC. Observe that EF = AD and AD = AC. This results in the fact that FDC is isosceles and \( \angle FDC = \pi - \angle EDA \).
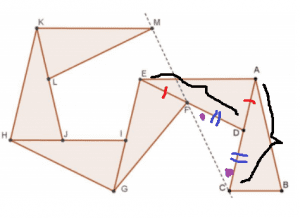[/et_pb_tab][et_pb_tab title="Hint 3" _builder_version="4.0"]Now, we will try to infer something about triangle MEF. Observe that KM || HI as \( \angle MKJ = \angle KJH\).
Hence KHIM must be a parallelogram. Hence, KH || MI.
Also, \( \angle KHI =\angle HIG \). Hence, KH || EG.
Hence, it implies from KH || MI and KH || EG, that M,E,I,G are collinear.
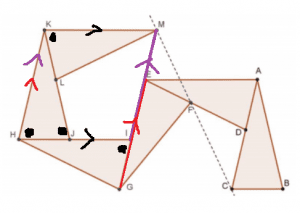[/et_pb_tab][et_pb_tab title="Hint 4" _builder_version="4.0"]Now, this diagram ends it all. Observe that MI = KH. Also, EI = LJ. Hence, ME = KL = EP.
Hence, MEF is isosceles.
Also, \( \angle MEF = \pi - \angle GEF = \pi - \angle EDA = \angle FDC \).
Hence, triangle MEF is similar to triangle FDC. This implies that \( \angle EFM = \angle DFC\).
QED
[/et_pb_tab][/et_pb_tabs][et_pb_text _builder_version="3.27.4" text_font="Raleway|300|||||||" text_text_color="#ffffff" header_font="Raleway|300|||||||" header_text_color="#e2e2e2" background_color="#0c71c3" custom_margin="48px||48px" custom_padding="20px|20px|20px|20px" border_radii="on|5px|5px|5px|5px" box_shadow_style="preset3"]Math Olympiad is the greatest and most challenging academic contest for school students. Brilliant school students from over 100 countries participate in it every year. Cheenta works with small groups of gifted students through an intense training program. It is a deeply personalized journey toward intellectual prowess and technical sophistication.[/et_pb_blurb][et_pb_button button_url="https://cheenta.com/matholympiad/" url_new_window="on" button_text="Learn More" button_alignment="center" _builder_version="3.23.3" custom_button="on" button_bg_color="#0c71c3" button_border_color="#0c71c3" button_border_radius="0px" button_font="Raleway||||||||" button_icon="%%3%%" background_layout="dark" button_text_shadow_style="preset1" box_shadow_style="preset1" box_shadow_color="#0c71c3"][/et_pb_button][et_pb_text _builder_version="3.27.4" text_font="Raleway|300|||||||" text_text_color="#ffffff" header_font="Raleway|300|||||||" header_text_color="#e2e2e2" background_color="#0c71c3" custom_margin="50px||50px" custom_padding="20px|20px|20px|20px" border_radii="on|5px|5px|5px|5px" box_shadow_style="preset3"]
