- This topic has 8 replies, 1 voice, and was last updated 1 year, 6 months ago by
 Arisha Roy.
Arisha Roy.
-
AuthorPosts
-
February 23, 2024 at 10:50 pm #99219
 Arisha RoyParticipant
Arisha RoyParticipantProblem 21
Alina writes the numbers \(1,2, \ldots, 9\) on separate cards, one number per card. She wishes to divide the cards into 3 groups of 3 cards so that the sum of the numbers in each group will be the same. In how many ways can this be done?
February 23, 2024 at 10:51 pm #99220 Arisha RoyParticipant
Arisha RoyParticipantSolution:
Sum of the numbers of the whole group will be,
\(1+2 \cdots+9=\frac{9(10)}{2}=45\)
After dividing the cards in 3 groups, the sum of the numbers in each group,
\(\frac{9\times10}{2}=45\)To make the counting easier, first we will make the possible groups in which there is 9. 2 groups can be posible i.e. \((9,2,4)\) and \((9,1,5)\).
We will repeat the same process for 8 using the remaining elements in the list.
Possible groups are \((8,2,5)\), \(8,1,6\), \(8,3,4\).
Again we will repeat the same process for 7 using the remaining elements in the list.
Possible groups are \((7,2,6)\), \(7,3,5\).
Again we will repeat the same process for 6 using the remaining elements in the list.
Possible groups are \((6,4,5)\).
We will not get any new set.
So, possible sets will be \((9,1,5)(8,3,4)(7,2,6)\) and \((9,2,4)(8,1,6)(7,3,5)\)
Answer: 2-
This reply was modified 1 year, 6 months ago by
 Arisha Roy.
Arisha Roy.
-
This reply was modified 1 year, 6 months ago by
 Arisha Roy.
Arisha Roy.
February 23, 2024 at 11:05 pm #99222 Arisha RoyParticipant
Arisha RoyParticipantProblem 22
In a sequence of positive integers, each term after the second is the product of the previous two terms. The sixth term in the sequence is 4000. What is the first term?
February 23, 2024 at 11:11 pm #99223 Arisha RoyParticipant
Arisha RoyParticipantSolution:
Let the 1st term is \(a\) and 2nd term is \(b\).
The 3rd term will be \(ab\).
The 4th term will be \(ab^2\).
The 5th term will be \(a^2b^3\).
The 6th term will be \(a^3b^5\).
So, the series will be, \(a\), \(b\), \(ab\), \(ab^2\), \(a^2b^3\), \(a^3b^5\).
So, \(a^3b^5 = 4000\)
\(\Rightarrow a^3b^5 = 5^32^5\)
\(\Rightarrow a=5\)
First term will be \(5\)
-
This reply was modified 1 year, 6 months ago by
 Arisha Roy.
Arisha Roy.
February 25, 2024 at 11:20 am #99258 Arisha RoyParticipant
Arisha RoyParticipantProblem 24
Isosceles \(\triangle A B C\) has equal side lengths \(A B\) and \(B C\). In the figure below, segments are drawn parallel to \(\overline{A C}\) so that the shaded portions of \(\triangle A B C\) have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height of \(h\) of \(\triangle A B C\) ?
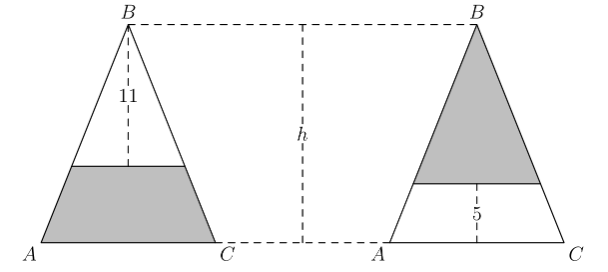
-
This reply was modified 1 year, 6 months ago by
-
AuthorPosts
- You must be logged in to reply to this topic.