[Deepan Dutta]

If \(A\) and \(B\) are vertices of a polyhedron, define the distance \(d(A, B)\) to be the minimum number of edges of the polyhedron one must traverse in order to connect \(A\) and \(B\). For example, if \(\overline{A B}\) is an edge of the polyhedron, then \(d(A, B)=1\), but if \(\overline{A C}\) and \(\overline{C B}\) are edges and \(\overline{A B}\) is not an edge, then \(d(A, B)=2\). Let \(Q, R\), and \(S\) be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of 20 equilateral triangles). What is the probability that \(d(Q, R)>d(R, S)\) ?

[Deepan Dutta]

If we observe the regular icosahedron carefully then we can understand that it has \(12\) vertices that can be divided into \(4\) layers,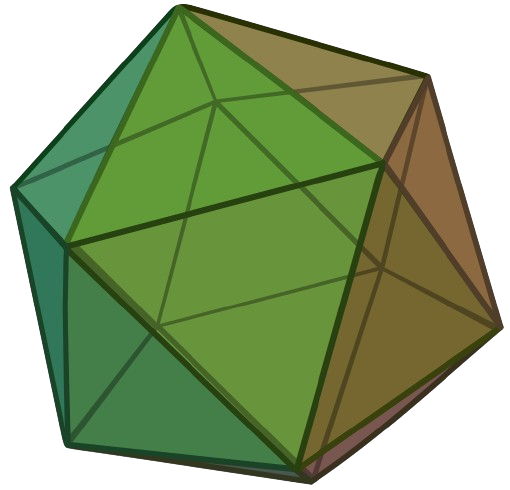

1. Top most point
2. Upper regular pentagon
3. Lower regular pentagon
4. Bottom most point.

So if we try to choose the top most point as \(R\), then there are \({5\choose1}\cdot{6\choose1}\) ways to choose the points \(S\) and \(Q\) respectively,when \(S\) is in the upper regular pentagon layer.

On the other hand If \(S\) is in the lower regular pentagon layer, then \(S\) and \(Q\) can be chosen in \({5\choose1}\cdot{1\choose1}\) ways.

 

\(\therefore\) Probability of choosing three points \(Q,R\) and \(S\) so that \(d(Q, R)>d(R, S)=\frac{{5\choose1}\cdot{6\choose1}+{5\choose1}\cdot{1\choose1}}{{11\choose2}\cdot2!}=\frac{35}{110}=\boxed{\frac{7}{22}}\).

[In \({12\choose1}\) ways we can choose the point \(R\), as that factor is present in both the numerator and denominator so we are not taking that under consideration]

• This reply was modified 1 year, 6 months ago by Deepan Dutta.

[Author]

Posts