Try this beautiful problem from Geometry based on Centroid.
\(\triangle ABC\) has centroid \(G\).\(\triangle ABG\),\(triangle BCG\), and \(\triangle CAG\) have centroids \(G_1\), \(G_2\), \(G_3\) respectively. The value of \(\frac{[G1G2G3]}{[ABC]}\) can BE represented by \(\frac{p}{q}\) for positive integers \(p\) and \(q\).
Find \(p+q\) where\([ABCD]\) denotes the area of ABCD.
Geometry
Triangle
centroid
But try the problem first...
Answer: \(10\)
Question Papers
Pre College Mathematics
First hint
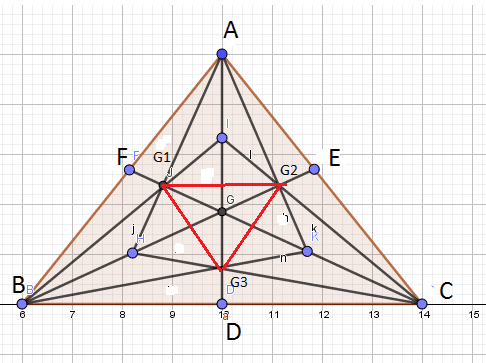
\(\triangle ABC\) has centroid \(G\).\(\triangle ABG\),\(triangle BCG\), and \(\triangle CAG\) have centroids \(G1\),\(G2\),\(G3\) respectively.we have to find out value of \(\frac{[G1G2G3]}{[ABC]}\) i.e area of \(\frac{[G1G2G3]}{[ABC]}\)
Let D, E, F be the midpoints of BC, CA, AB respectively.
Area of $\frac{[DEF]}{[ABC]}$=$\frac{1}{4}$
we know that any median is divided at the centroid $2:1$. Now can you find out \(GG_1,GG_2,GG_3\) ?
Can you now finish the problem ..........
Second Hint
we know that any median is divided at the centroid $2:1$
Now $G_1$ is the centroid of $\triangle ABG$, then$GG_1=2G_1F$
Similarly,$GG_2 = 2G_2D$ and$GG_3 = 2G_3E$
Thus, From homothetic transformation $\triangle G_1G_2G_3$ maps to $\triangle FDE$ by a homothety of ratio$\frac{2}{3}$
Therefore,$\frac{[G_1G_2G_3]}{[DEF]}$ = $(\frac{2}{3})^2$=$\frac{4}{9}$
can you finish the problem........
Final Step
Therefore we say that $\frac{[G_1G_2G_3]}{[ABC]}$ = $\frac{[G_1G_2G_3]}{[DEF]}\cdot \frac{[DEF]}{[ABC]} $= $\frac{4}{9}\cdot \frac{1}{4}$=$\frac{1}{9}$=$\frac{p}{q}$
So $p+q$=$9+1$=\(10\)
AMC - AIME Boot Camp... for brilliant students.
Use our exclusive one-on-one plus group class system to prepare for Math Olympiad
