Australian Mathematics Competition - 2023 - Upper Primary Division - Grades 5 & 6- Questions and Solutions

Problem 1:

This shape is made from 7 squares, each 1 cm by 1 cm . What is its perimeter?

(A) 7 cm (B) 12 cm (C) 14 cm (D) 16 cm (E) 28 cm

Problem 2:

There are five shapes here. How many are quadrilaterals?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 3:

In a board game, Nik rolls three standard dice, one at a time. He needs his three rolls to add to 12 . His first two dice rolls are 5 and 3 . What does he need his third roll to be?

(A) 2 (B) 3 (C) 4 (D) 5 (E) 6

Problem 4:

In this diagram, how many of the small squares need to be shaded for the large rectangle to be one-quarter shaded?

(A) 2 (B) 3 (C) 4 (D) 6 (E) 12

Problem 5:

Petra left for school at 8:51 am. She got to school at 9:09 am. How long did it take Petra to get to school?

(A) 9 minutes (B) 10 minutes (C) 18 minutes (D) 42 minutes (E) 1 hour

Problem 6:

Which letter marks where 25 is on this number line?

Problem 7:

This bottle holds 4 glasses of water.

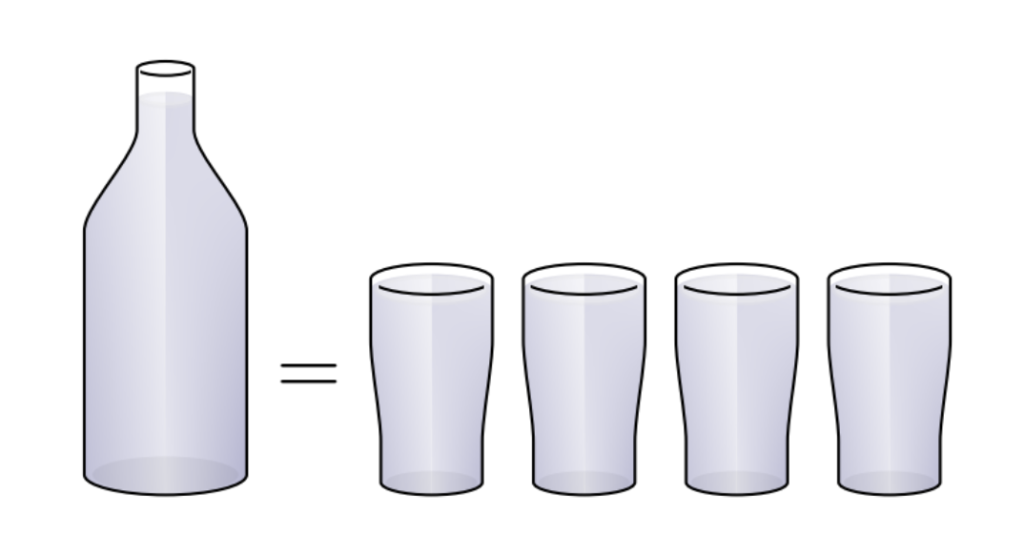
Which one of the following holds the most water?

Problem 8:

Two pizzas are shared equally between 3 students. What fraction of a whole pizza does each student get?

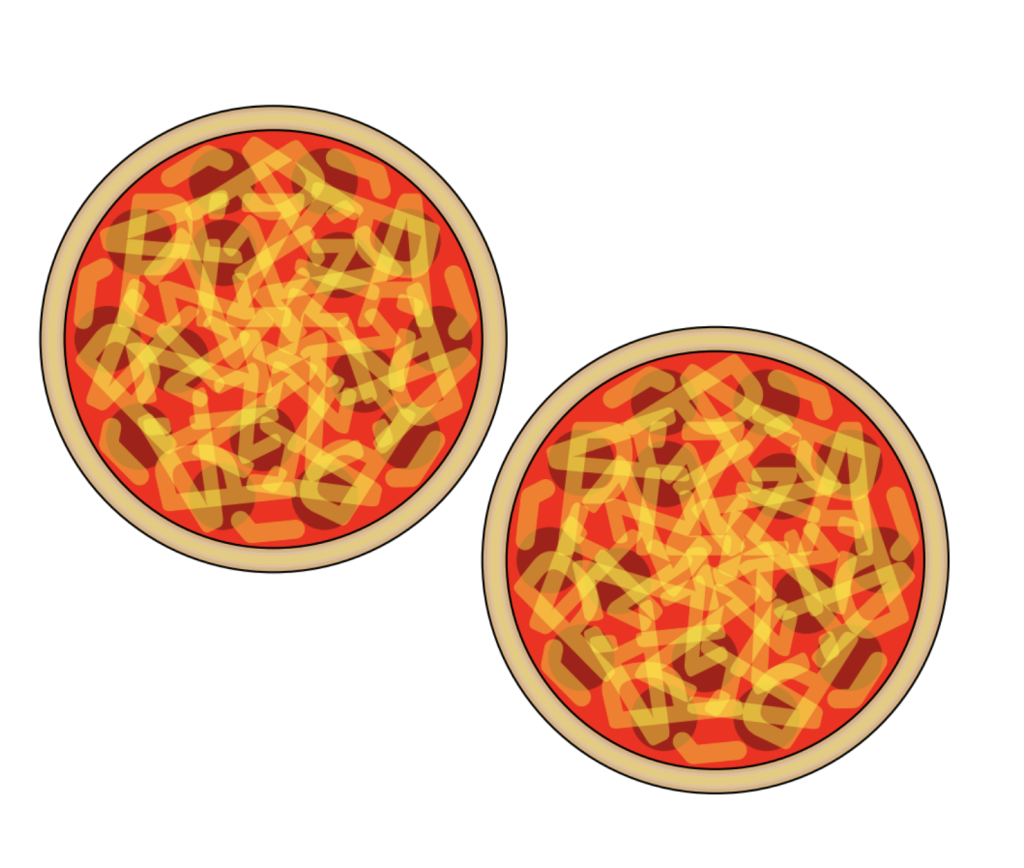
(A) $\frac{1}{2}$ (B) $\frac{1}{3}$ (C) $\frac{1}{4}$ (D) $\frac{2}{3}$ (E) $\frac{3}{4}$

Problem 9:

A piece of card is cut out and labelled as shown in the diagram.

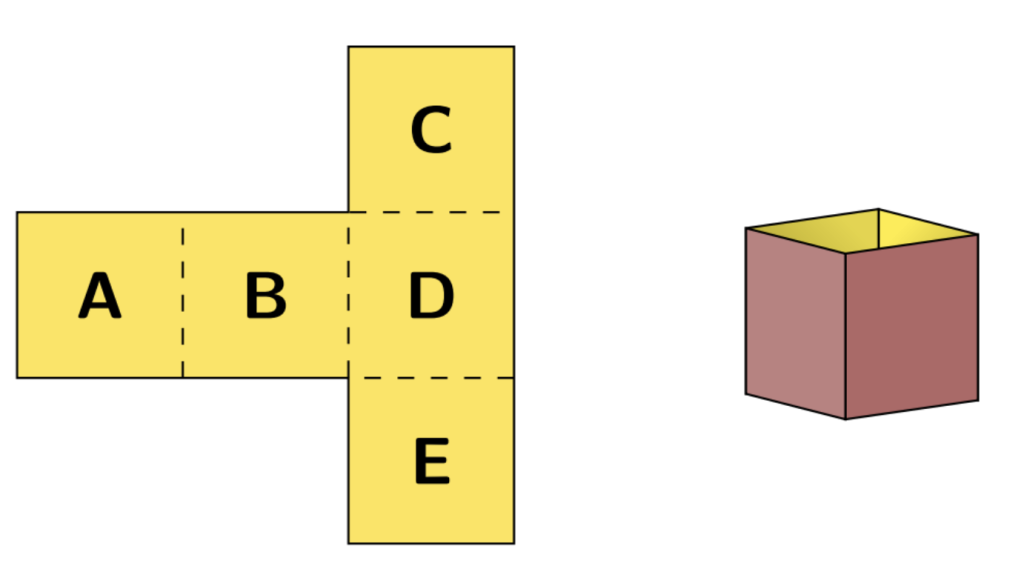
It is folded along the dotted lines to make a box without a top. Which letter is on the bottom of the box?

(A) A (B) B (C) C (D) D (E) E

Problem 10:

Doughnuts come in bags of 3 and boxes of 8 . I bought exactly 25 doughnuts for my party.What do I get when I add the number of boxes I bought and the number of bags I bought?

(A) 4 (B) 5 (C) 6 (D) 7 (E) 8

Problem 11:

This line graph shows the temperature each hour during a day.

Roughly for how long was the temperature above $20^{\circ} \mathrm{C}$ ?

(A) 7 hours (B) 8 hours (C) 9 hours (D) 10 hours (E) 11 hours

Problem 12:

VIV takes her three children, HANNAH, OTTO and IZZI, out shopping. Each is wearing a t-shirt with their name on the front in capital letters. When they stand in front of the shop mirror, which names appear the same in the reflection as on the shirts?

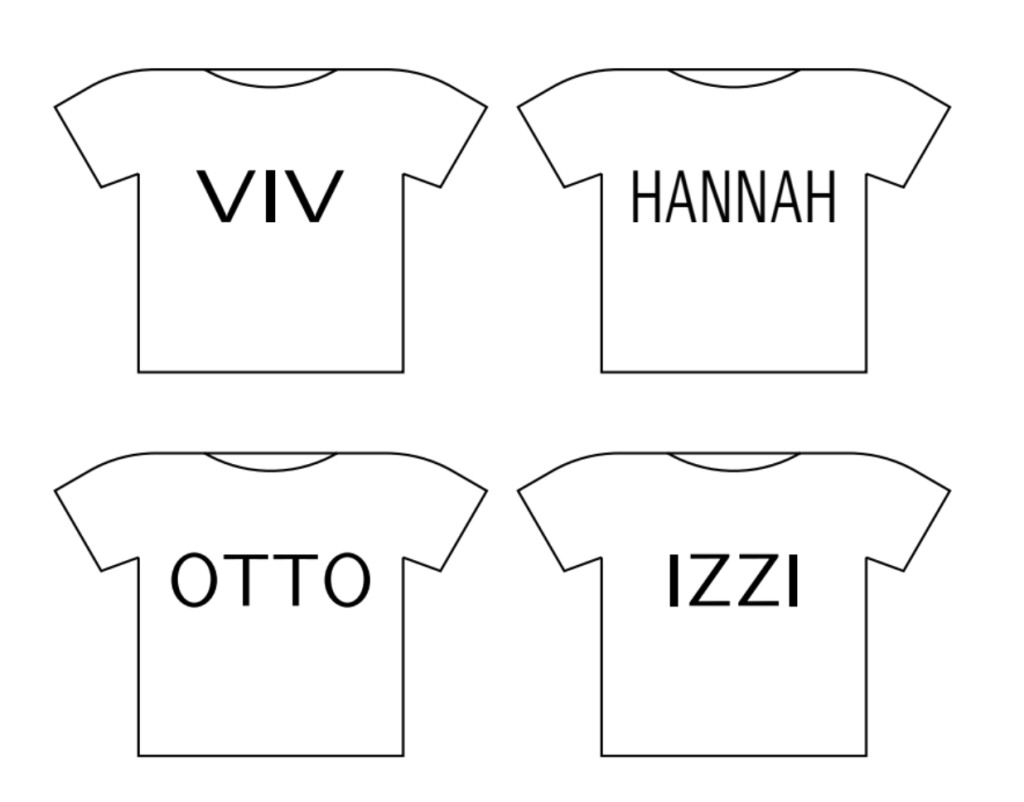
(A) VIV and OTTO (B) VIV, OTTO and IZZI (C) VIV, HANNAH and IZZI (D) HANNAH and OTTO (E) All four of them

Problem 13:

This regular hexagon has angles of $120^{\circ}$ and the square has angles of $90^{\circ}$.

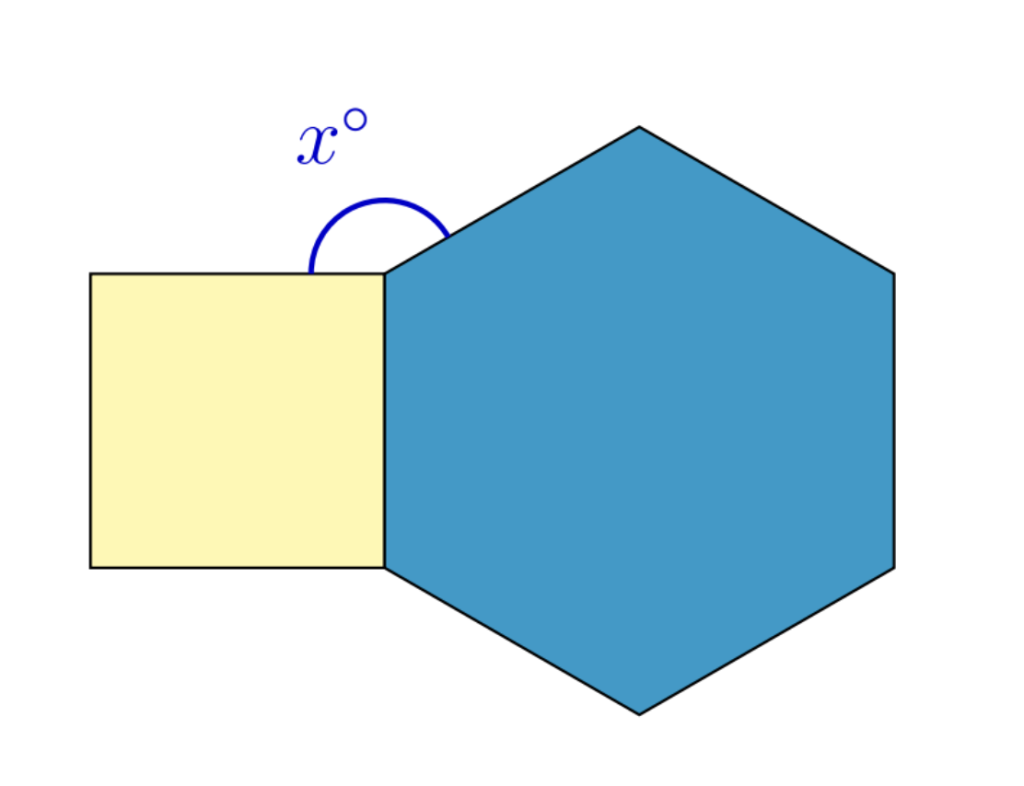
What is the angle $x^{\circ}$ in the diagram?

(A) $90^{\circ}$ (B) $120^{\circ}$ (C) $135^{\circ}$ (D) $150^{\circ}$ (E) $180^{\circ}$

Problem 14:

Syed's mother had some money to share with her family. She gave one-quarter of her money to Syed. Then she gave one-third of what was left to Ahmed. Then she gave one-half of what was left to Raiyan. She was left with $\$ 15$, which she kept for herself. How much money did Syed's mother have to start with?

(A) $\$ 30$ (B) $\$ 45$ (C) $\$ 60$ (D) $\$ 90$ (E) $\$ 120$

Problem 15:

The rectangle shown has a side length of 9 cm . It is divided into 3 identical rectangles as shown. What is the area, in square centimetres, of the original rectangle?

(A) 45 (B) 50 (C) 52 (D) 54 (E) 63

Problem 16:

This diagram shows a rectangle with a perimeter of 30 cm . It has been divided by 2 lines into 4 small rectangles. Three of the small rectangles have the perimeters shown. What is the perimeter of fourth small rectangle?

(A) 10 cm (B) 12 cm (C) 14 cm (D) 16 cm (E) 18 cm

Problem 17:

There are 10 questions in a test. Each correct answer scores 5 points, each wrong answer loses 3 points, and if a question is left blank it scores 0 points. Tycho did this test and scored 27 points. How many questions did Tycho leave blank?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Problem 18:

Estelle is making decorations shaped like the 8-pointed star shown. She folds a square of paper to make a triangle with 8 layers as shown.

How could she cut the triangle so that the unfolded shape is the star?

Problem 19:

Earlier this year Ben said, 'Next year I will turn 13 , but 2 days ago I was $10 . '$ Ben's birthday is

(A) 1st January (B) 2nd January (C) 29th December (D) 30th December (E) 31st December

Problem 20:

Peyton, Luka and Dan have 180 stickers in total. Peyton has half as many stickers as Luka. Dan has three times as many as Luka.
How many stickers does Peyton have?

(A) 20 (B) 24 (C) 30 (D) 40 (E) 54

Problem 21:

Mrs Graaf invents a game for her students to practise arithmetic. They roll two 10 -sided dice to pick two random numbers. Starting at one of the numbers, they keep adding the other number until they reach a 3-digit number. Ian rolls a 5 and an 8 . If he chooses to start with 5 and then add 8 again and again, his list is $5,13,21, \ldots$, 93,101 . If he chooses to start with 8 and add 5 , his list is $8,13,18, \ldots, 98,103$ On Nara's turn, she makes a list that ends with 107. What pair of numbers could she have rolled?

(A) 4 and 8 (B) 5 and 7 (C) 3 and 4 (D) 6 and 9 (E) 3 and 8

Problem 22:

At a school concert, the tickets cost $\$ 20$ per adult and $\$ 2$ per child. The total paid by the 100 people who attended was $\$ 920$. How many were children?

(A) between 25 and 35 (B) between 35 and 45 (C) between 45 and 55 (D) between 55 and 65 (E) between 65 and 75

Problem 23:

Meena has a standard dice, with each pair of opposite faces adding to 7 . At first, the three faces she can see add to 6 , as shown. She holds the dice between a pair of opposite faces and rotates it $180^{\circ}$, keeping these opposite faces facing the same direction. She puts the dice back down and adds up the three faces she can now see.

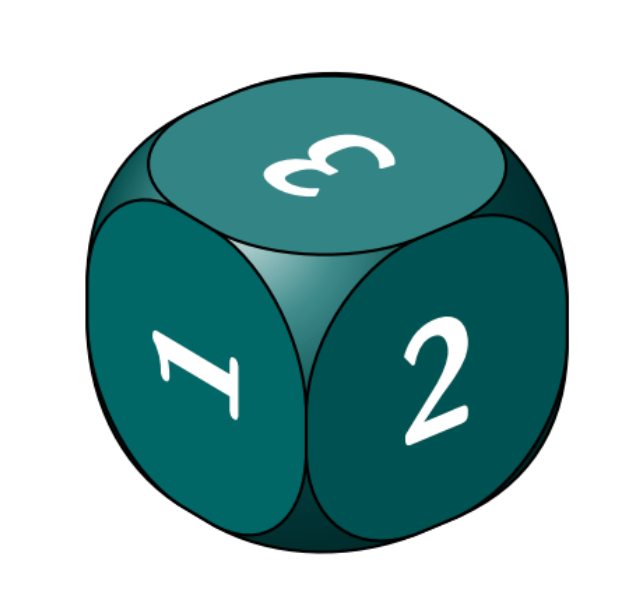
What is the smallest possible total she could get?

(A) 6 (B) 8 (C) 10 (D) 12 (E) 14

Problem 24:

I have 4 whole numbers that add up to 98. If I were to add 6 to the first number, subtract 6 from the second number, multiply the third number by 6 and divide the fourth number by 6, the four answers would all be the same. What is the sum of the largest two of my original four numbers?

(A) 72 (B) 86 (C) 88 (D) 90 (E) 94

Problem 25:

When I ride my bike at 20 kilometres per hour, each wheel turns at 2 revolutions per second. When I ride 1 kilometre, how many revolutions does each wheel make?

(A) 40 (B) 240 (C) 320 (D) 360 (E) 420

Problem 26:

Problem 27:

Li attempted to multiply a single-digit number by 36 , but he accidentally multiplied by 63 instead. His answer was 189 larger than the correct answer. What was the correct answer to the multiplication?

Problem 28:

Using 9 out of the 10 possible digits Safia writes 3 numbers, each between 100 and 999. She adds her 3 numbers together. What is the smallest possible sum?

Problem 29:

Yifan has a construction set consisting of red, blue and yellow rods. All rods of the same colour are the same length, but differently coloured rods are different lengths. She wants to make quadrilaterals using these rods.

• When she uses two red, one blue and one yellow rod, the perimeter of the quadrilateral is 36 cm .
• When she uses two blue, one red and one yellow rod, the perimeter is 35 cm .
• When she uses two yellow, one blue and one red rod, the perimeter is 33 cm .

What number do you get when you multiply the lengths of one red rod, one blue rod and one yellow rod?

Problem 30:

Janus is making patterns using square tiles. Each pattern is made by copying the previous pattern, then adding a tile to every grid square that shares an edge with the copied pattern.

His last pattern is the largest one that can be made with fewer than 1000 tiles. How many tiles are in this last pattern?