Australian Mathematics Competition - 2023 - Senior years 11 -12 Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat is the value of \(2023-3202\) ?
(A) -1221
(B) -1179
(C) 1179
(D) 1221
(E) 5225
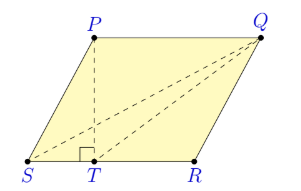
A parallelogram \(P Q R S\) has an area of \(60 \mathrm{~cm}^2\) and side \(P Q\) of length 10 cm .
Which length is 6 cm ?
(A) \(R Q\)
(B) \(R S\)
(C) \(Q T\)
(D) \(P T\)
(E) \(Q S\)
Which one of these is equal to \(57 \times 953\) ?
(A) 321
(B) 4321
(C) 54321
(D) 654321
(E) 7654321
What is the difference between \(2^5\) and \(5^2\) ?
(A) 0
(B) 1
(C) 3
(D) 5
(E) 7

What is the value of the angle \(\theta^{\circ}\) in the diagram?
(A) \(100^{\circ}\)
(B) \(110^{\circ}\)
(C) \(120^{\circ}\)
(D) \(130^{\circ}\)
(E) \(140^{\circ}\)

The shaded square is inscribed in the larger square as shown.
What is the ratio of shaded to unshaded area in the diagram?
(A) \(5: 4\)
(B) \(25: 24\)
(C) \(3: 2\)
(D) \(7: 4\)
(E) \(12: 7\)
Jemmy multiplies together all the integers from 1 to 18 . What are the last three digits of the result?
(A) 000
(B) 020
(C) 200
(D) 080
(E) 800
A fuel tank is \(40 \%\) empty. Then 40 litres of fuel is removed. The tank is now \(40 \%\) full. How many litres are in a full tank?
(A) 40
(B) 100
(C) 160
(D) 200
(E) 400
The volume \(V\) of a sphere of radius \(r\) is given by \(V=\frac{4}{3} \pi r^3\). For a sphere of volume \(V=100 \mathrm{~cm}^3\), which of the following is closest to the radius?
(A) 2.9 cm
(B) 3.5 cm
(C) 5 cm
(D) 5.8 cm
(E) 10 cm
If I add 3 consecutive odd integers, I get a total of \(9 m+3\). The largest of these 3 integers is
(A) \(3 m-3\)
(B) \(3 m-1\)
(C) 3 m
(D) \(3 m+1\)
(E) \(3 m+3\)
The value of \(\left(\sqrt{24} + \sqrt{54}\right)^2\) is
(A) 140
(B) 150
(C) 160
(D) 170
(E) 180
In a group of 6 people there are 3 pairs of twins. How many 3 -member committees can be chosen that do not contain any pair of twins?
(A) 0
(B) 8
(C) 12
(D) 24
(E) 48
Assuming \(a>b>0\), the expression \(\frac{a^{-1}-b^{-1}}{a^{-2}-b^{-2}}\) can be written as
(A) \(\frac{b-a}{a b}\)
(B) \(\frac{b+a}{a b}\)
(C) \(\frac{a b}{b+a}\)
(D) \(\frac{a^2-b^2}{a-b}\)
(E) \(a-b\)
A bag contains red and yellow balls such that the ratio red : yellow is (5: 7). Then 10 balls of each colour are removed and the ratio changes to (5: 8). How many balls were originally in the bag?
(A) 48
(B) 60
(C) 72
(D) 84
(E) 96
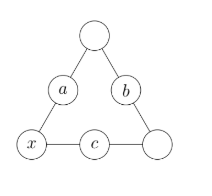
In the solution to this number puzzle, whenever there are three numbers in a straight line, the middle number is the sum of the other two.
What is the value of \(x\) ?
(A) \(\frac{1}{2}(a+b+c)\)
(B) \(\frac{1}{2}(b-a-c)\)
(C) \(\frac{1}{2}(a+b-c)\)
(D) \(\frac{1}{2}(a-b+c)\)
(E) \(\frac{1}{2}(b+c-a)\)
If \(f(x)=5+x\) and \(g(x)=7-x\), then \(f(g(x))-g(f(x))\) equals
(A) \(10-x\)
(B) 7
(C) \(x+2\)
(D) 10
(E) \(2 x-2\)
The hypotenuse of a right-angled triangle has length 6 cm . The perimeter of the triangle is 14 cm .
What is the area of the triangle in square centimetres?
(A) 7
(B) 12
(C) 14
(D) 21
(E) 24

I have two identical dice, each with faces
\(1, \frac{1}{2}, \sqrt{3}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{2}}\) and \(\frac{\sqrt{3}}{2}\).
I roll both dice and multiply the two numbers rolled, then simplify my answer. What is the probability that this product is rational?
(A) \(\frac{1}{9}\)
(B) \(\frac{1}{6}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{5}{18}\)
(E) \(\frac{7}{18}\)
How many distinct pairs \((x, y)\) satisfy \(x^2+y^2<50\) if \(x\) and \(y\) are both positive integers with \(x>y\) ?
(A) 15
(B) 13
(C) 11
(D) 9
(E) 8

A \(15 \mathrm{~cm} \times 20 \mathrm{~cm}\) rectangle is cut into two triangles. One triangle is rotated and placed on top of the other triangle as shown to form a concave pentagon.
What is the perimeter of the pentagon?
(A) 80 cm
(B) 84 cm
(C) 93 cm
(D) 96 cm
(E) 105 cm
I have four numbers. When I add 3 to the first number, subtract 3 from the second number, multiply the third number by 3 and divide the fourth number by 3 , my four answers are all equal.
My original 4 numbers added to 32 . What is the sum of the largest two of these?
(A) 24
(B) 25
(C) 26
(D) 27
(E) 28
Antonio walked 11.5 km to his cousin Maria's house.
At first he walked uphill, then along a flat part of the road and the final part was downhill. The trip took 2 hours 54 minutes. The next day his walk back home took 3 hours 6 minutes. Antonio walks uphill at a constant speed of \(3 \mathrm{~km} / \mathrm{h}\), on the flat at \(4 \mathrm{~km} / \mathrm{h}\) and downhill at \(5 \mathrm{~km} / \mathrm{h}\).
What is the length, in kilometres, of the flat part of the road?
(A) 4
(B) 4.5
(C) 5
(D) 5.5
(E) 6
I think of two positive integers and call their sum \(S\) and their product \(P\). Which one of the following could not be the value of \(S+P\) ?
(A) 84
(B) 86
(C) 88
(D) 90
(E) 92

A solid regular tetrahedron has 4 faces, each an equilateral triangle. It is suspended in the entomology laboratory. There are two food sources on the tetrahedron, one at a vertex \(V\) and the other at \(X\), the centre of the opposite face. When a geodesic grub is placed anywhere upon the tetrahedron, it instinctively crawls along the shortest possible path over the surface to the closest food source.
What fraction of the surface area is closer to \(V\) than to \(X\), in terms of paths along the surface?
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{2}{3}\)
(E) \(\frac{3}{4}\)
Three spheres of radius 2 sit on a flat surface touching one another. A smaller sphere sits on the same surface, in the middle and touching all three of the bigger spheres. What is its radius?
(A) \(2 \sqrt{3}-2 \sqrt{2}\)
(B) \(2 \sqrt{\sqrt{3}-\sqrt{2}}\)
(C) \(\sqrt{3}\)
(D) \(\frac{3}{2}\)
(E) \(\frac{2}{3}\)
How many ways can you select four distinct equally spaced numbers from the set \({1, \ldots, 40} ?\)
Digits \(a, b\) and \(c\) are chosen and then two six-digit numbers are formed, \(M\) with digits \(a b c a b c\) and \(N\) with digits ababab. The ratio \(M: N) is (55: 54\). What is the 3-digit number \(a b c\) ?

Two wheels are fixed to an axle as shown. Due to their different sizes, the two wheels trace two concentric circles when rolled on level ground.
In centimetres, what is the radius of the circle traced on the ground by the larger wheel?
Martin the gardener has 3 new vegetable beds, near the kitchen, laundry and shed. Each year he will plant one bed with tomatoes, one with beans, and one with carrots. He needs a schedule for planting that goes for 8 summers. To balance the disease risk and soil nutrients, his schedule must follow these rules:
In how many ways can he schedule his vegetable planting for these 8 summers?
A percussionist is practising patterns within an 11-beat bar of music. To visualise this, she arranges 11 dots around a circle, with black dots representing a drum hit. She reads this pattern of dots clockwise, starting at the top.
Her patterns have at least one black dot, no two adjacent black dots and two patterns only count as the same if they are the same in every detail, including where the pattern starts in the circle and the direction it is read.
For instance, patterns \(A\) and \(B\) below are two of her patterns, and they count as different, even though \(B\) can be thought of as \(A\) starting on a different beat. Pattern \(C\) is not one of her patterns, since it has two adjacent black dots.
How many drumming patterns like this are possible?
