Australian Mathematics Competition - 2022 - Upper Primary Division - Grades 5 & 6- Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat number is two hundred and five thousand, one hundred and fifty?
(A) 150 (B) 205 (C) 20150 (D) 25150 (E) 205150
What fraction of this picture is shaded?
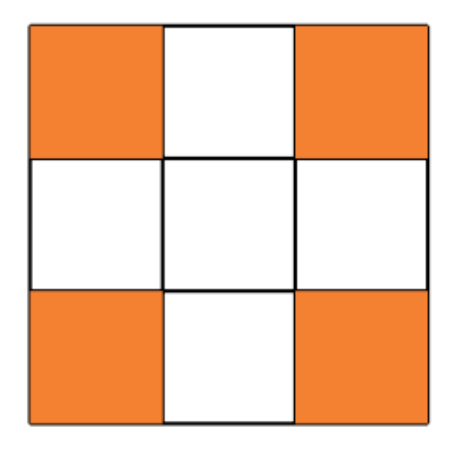
(A) $\frac{1}{2}$ (B) $\frac{2}{3}$ (C) $\frac{3}{4}$ (D) $\frac{4}{9}$ (E) $\frac{5}{9}$
$2220-2022=$
(A) 18 (B) 188 (C) 198 (D) 200 (E) 202
Audrey wrote these three numbers in order from smallest to largest:
$$
\begin{array}{llll}
1.03 & 0.08 & 0.4
\end{array}
$$
In which order did she write them?
(A) $0.08,1.03,0.4$ (B) $0.08,0.4,1.03$ (C) $0.4,0.08,1.03$
(D) $0.4,1.03, .008$ (E) $1.03,0.4,0.08$
I was 7 years old when my brother turned 3. How old will I be when
he turns 7?
(A) 9 (B) 10 (C) 11 (D) 12 (E) 13
This shape is built from 29 squares, each $1 \mathrm{~cm} \times 1 \mathrm{~cm}$. What is its perimeter in centimetres?

(A) 52 (B) 58 (C) 60 (D) 68 (E) 72
A tachometer indicates how fast the crankshaft in a car's engine is spinning, in thousands of revolutions per minute (rpm). What is the reading on the tachometer shown?

(A) 2.2 rpm (B) 2.4 rpm (C) 240 rpm (D) 2200 rpm (E) 2400 rpm
Joseph had a full, one-litre bottle of water. He drank 320 millilitres of it. How much was left?
(A) 660 mL (B) 670 mL (C) 680 mL (D) 730 mL (E) 780 mL
Which of these rectangles has an area of 24 square centimetres?
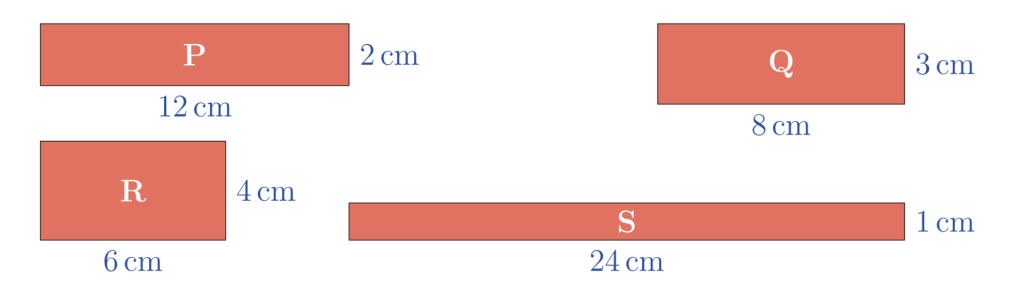
(A) Q only (B) Q and R only (C) R only (D) S only (E) P, Q, R and S
This table shows Jai's morning routine. If he needs to be at school by $8: 55 \mathrm{am}$ what is the latest time he can start his shower?

(A) 7:35 am (B) 7: 50 am (C) 8:05 am (D) 8:20 am (E) 8:35 am
Which spinner is twice as likely to land on red as white?

Starting at 0 on the number line, Clement walks back and forth in the following pattern: 3 to the right, 2 to the left, 3 to the right, 2 to the left, and so on.
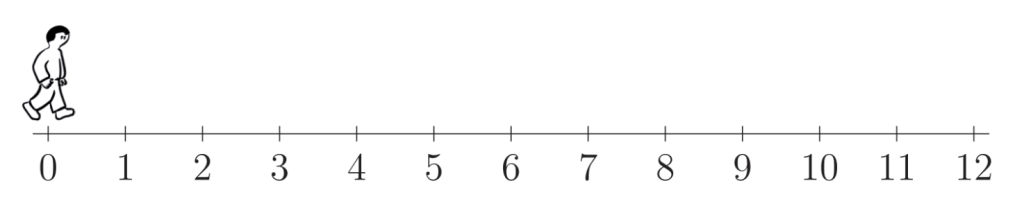
How many times does he walk past the position represented by $4 \frac{1}{2}$ ?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
Three digits are missing from this sum. Toby worked out the missing numbers and added them together. What was his answer?
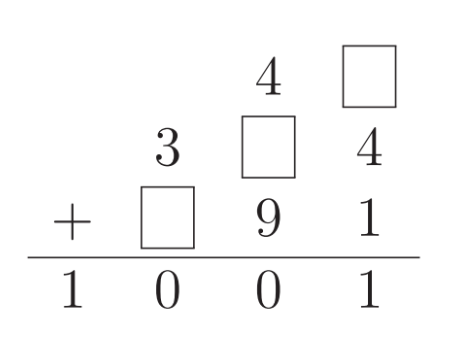
(A) 11 (B) 13 (C) 15 (D) 17 (E) 19
I have three cardboard shapes: a square, a circle and a triangle. I glue them on top of each other as shown in this diagram.
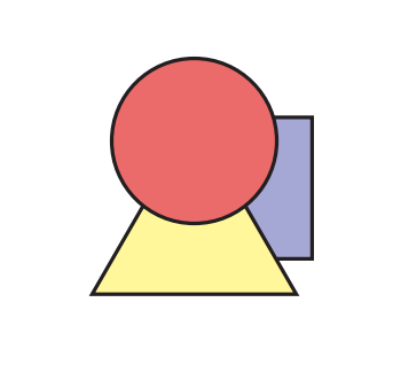
I then flip the glued-together shapes over. What could they look like?

What is the missing number needed to make this number sentence true? $270 \div 45=\square \div 15$
(A) 3 (B) 6 (C) 60 (D) 90 (E) 150
Three different squares are arranged as shown. The perimeter of the largest square is 32 centimetres. The area of the smallest square is 9 square centimetres. What is the perimeter of the mediumsized square?
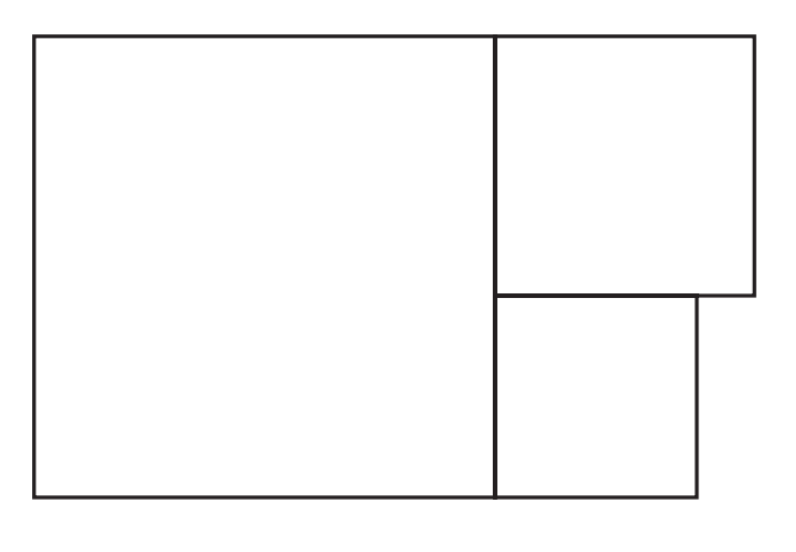
(A) 12 cm (B) 14 cm (C) 20 cm (D) 24 cm (E) 30 cm
Huang has a bag of marbles. Mei takes out one-third of them. Huang then takes out one-half of those left, leaving 8 marbles in the bag. How many marbles were originally in the bag?
(A) 12 (B) 16 (C) 18 (D) 24 (E) 36
A different positive whole number is placed at each vertex of a cube. No two numbers joined by an edge of the cube can have a difference of 1.
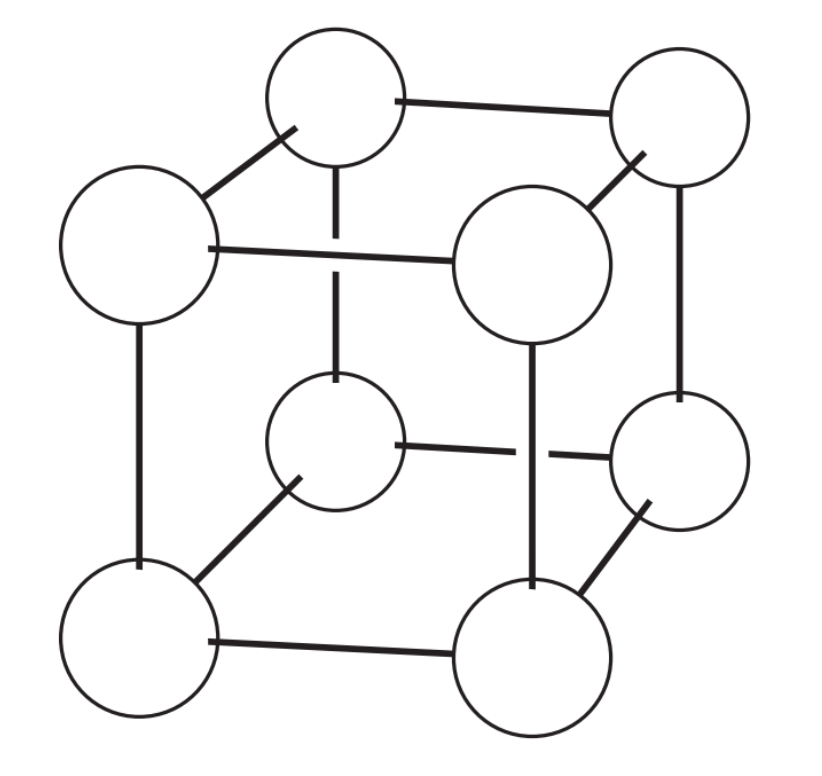
What is the smallest possible sum of the eight numbers?
(A) 36 (B) 37 (C) 38 (D) 39 (E) 40
George is 78 this year. He has three grandchildren: Michaela, Tom and Lucy. Michaela is 27 , Tom is 23 and Lucy is 16 . After how many years will George's age be equal to the sum of his grandchildren's ages?
(A) 3 (B) 6 (C) 9 (D) 10 (E) 12
Ms Graham asked each student in her Year 5 class how many television sets they each have This graph shows the results.
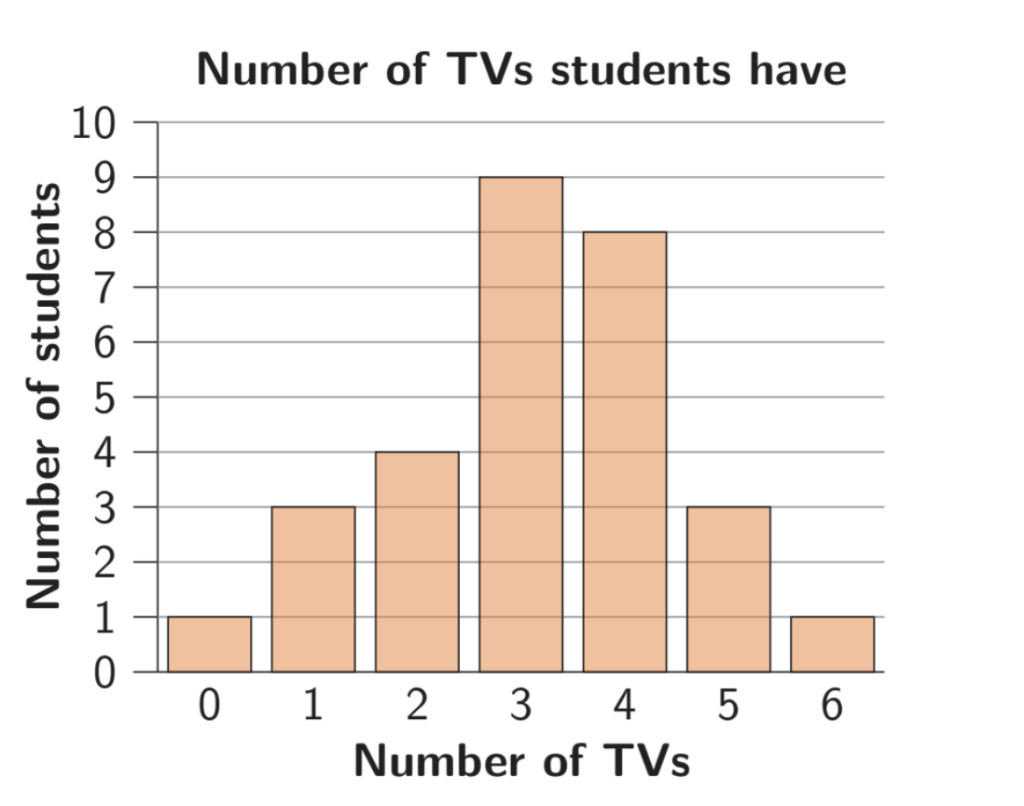
How many television sets do the students have altogether?
(A) 9 (B) 29 (C) 91 (D) 99 (E) 101
In a mathematics competition, 70 boys and 80 girls competed. Prizes were won by 6 boys and $15 \%$ of the girls. What percentage of the students were prize winners?
(A) $10 \%$ (B) $12 \%$ (C) $15 \%$ (D) $18 \%$ (E) $20 \%$
Ariel writes the letters of the alphabet on a piece of paper as shown She turns the page upside down and looks at it in her bathroom mirror. How many of the letters appear unchanged when viewed this way?

(A) 0 (B) 3 (C) 4 (D) 6 (E) 9
The Australian Mathematical College (AMC) has 1000 students. Each student takes 6 classes a day. Each teacher teaches 5 classes per day with 25 students in each class. How many teachers are there at the AMC?
(A) 40 (B) 48 (C) 50 (D) 200 (E) 240
This list pqrs, pqsr, prqs, prsq, … can be continued to include all 24 possible arrangements of the four letters $p, q, r$ and $s$. The arrangements are listed in alphabetical order. Which one of the following is 19th in this list?
(A) $s p q r$ (B) $s r p q$ (C) $q p s r$ (D) $q r p s$ (E) $r p s q$
In this puzzle, each circle should contain an integer. Each of the five lines of four circles should add to 40. When the puzzle is completed, what is the largest number used?
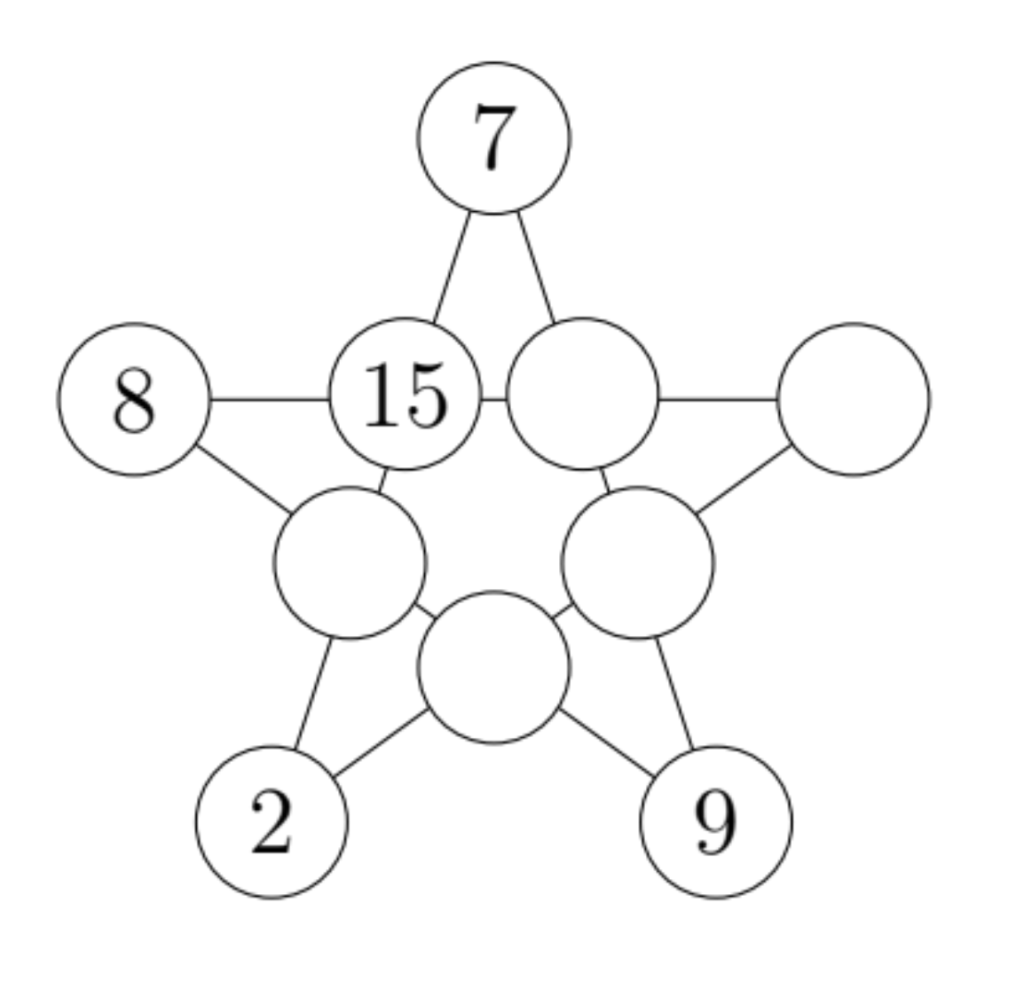
(A) 15 (B) 16 (C) 17 (D) 18 (E) 19
Nguyen writes down some numbers according to the following rules. Starting with the number 1, he doubles the number and adds 4 , so the second number he writes is 6 . He now repeats this process, starting with the last number written, doubling and then adding 4, but he doesn't write the hundreds digit if the number is bigger than 100 . What is the 2022nd number that Nguyen writes down?
Karen's mother made a cake for her birthday. After it was iced on the top and the 4 vertical faces, it was a cube with 20 cm sides. Darren was asked to decorate the cake with chocolate drops. He arranged them all over the icing in a square grid pattern, spaced with centres 2 cm apart. Those near the edges of the cube had centres 2 cm from the edge. The diagram shows one corner of the cake.
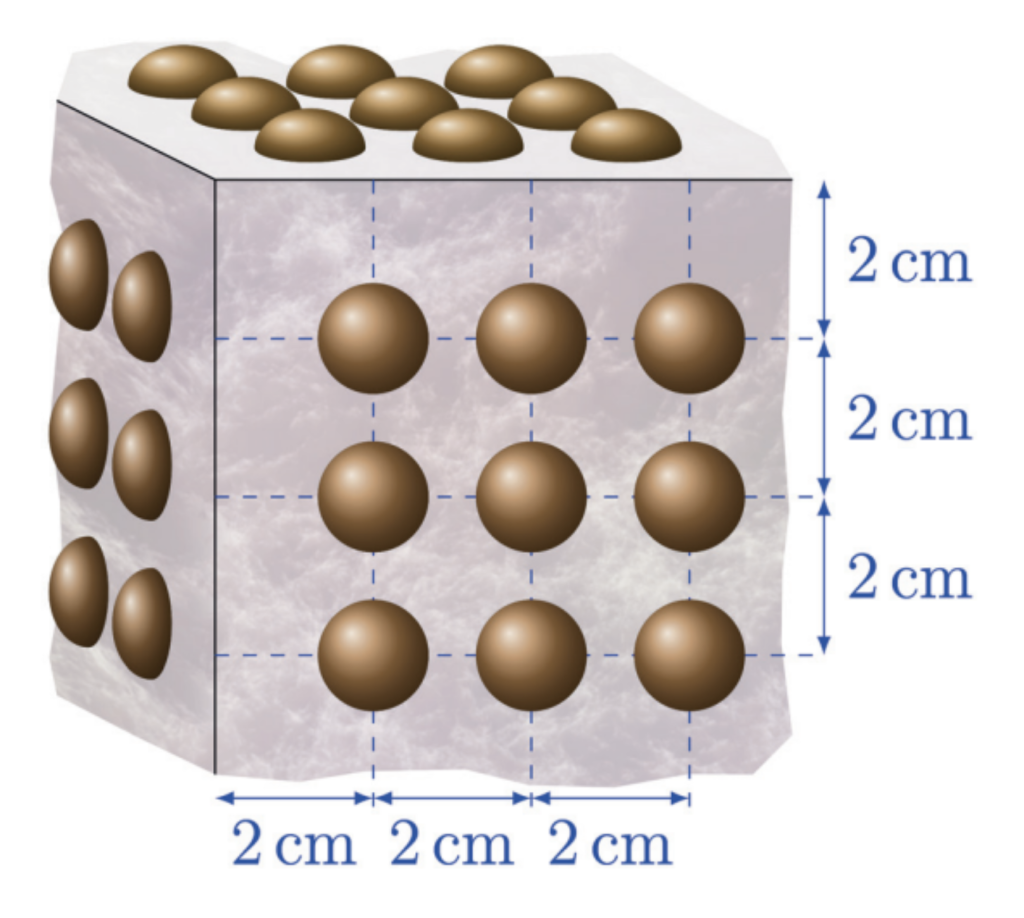
How many chocolate drops did Darren use to decorate Karen's cake?
I choose three different numbers out of this list and add them together:
$$
1,3,5,7,9, \ldots, 105
$$
How many different totals can I get?
The Athletics clubs of Albury and Wodonga agree to send a combined team to the regional championships. They have 11 sprinters on the combined team, 5 from Albury and 6 from Wodonga. For the $4 \times 100$ metre relay, they agree to have a relay team with two sprinters from the Albury club and two sprinters from the Wodonga club. How many relay teams are possible?
The following is a net of a rectangular prism with some dimensions, in centimetres, given.
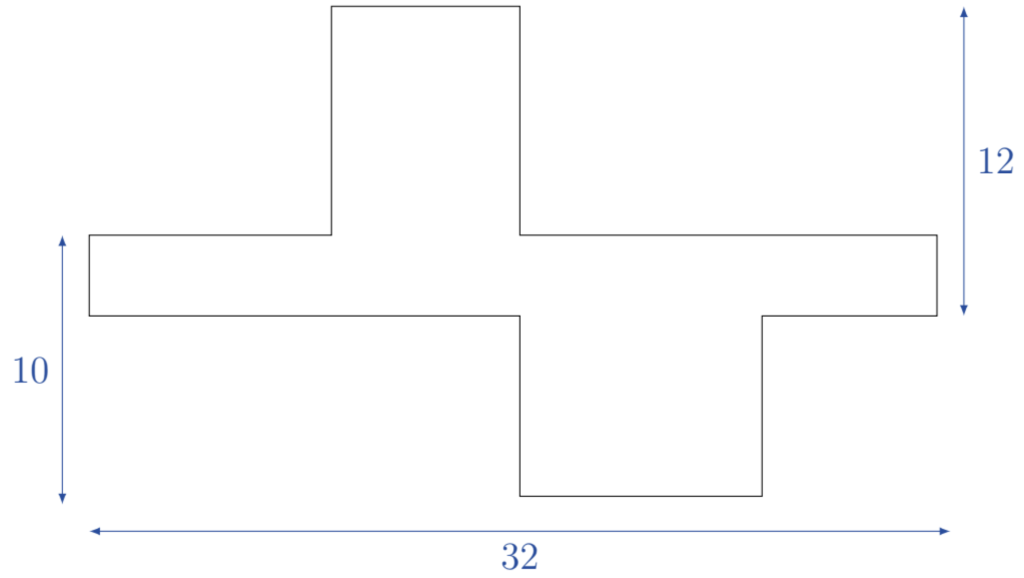
What is the volume of the rectangular prism in cubic centimetres?