Australian Mathematics Competition - 2021 - Senior years 11 -12 Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free Resources
Each small triangle is the same size.
What fraction of the largest triangle is shaded?
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{2}{5}\)
(E) \(\frac{3}{8}\)
When 2021 is divided by 7 the remainder is
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
What is \(12^1-12^{-1}-12^0\) ?
(A) 0
(B) 1
(C) \(10 \frac{11}{12}\)
(D) 11
(E) \(11 \frac{1}{12}\)

In this diagram, what is the size of the angles marked \(\theta\) ?
(A) \(70^{\circ}\)
(B) \(75^{\circ}\)
(C) \(80^{\circ}\)
(D) \(85^{\circ}\)
(E) \(90^{\circ}\)
The value of \(\frac{(20 \times 21)+21}{21}\) is
(A) 20
(B) 21
(C) 22
(D) 41
(E) 42
Henry's electric scooter took him 1.5 km in 3 minutes and 45 seconds.
What was the average speed of Henry's trip in kilometres per hour?
(A) 20
(B) 21
(C) 24
(D) 25
(E) 30
\(\frac{8^3 \times 3^6}{6^5}=\)
(A) 6
(B) 48
(C) 72
(D) 128
(E) 256
The product of recurring decimals \(0 . \dot{3}\) and \(0 . \dot{6}\) is the recurring decimal \(0 . \dot{x}\). What is the value of \(x\) ?
(A) 1
(B) 2
(C) 5
(D) 7
(E) 9

The parallelogram shown has an area of 48 square units. The value of \(a\) is
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11
Mervin is allowed to paint the four walls and the ceiling of his rectangular bedroom as he wishes, subject to the following constraints. He paints each surface in one of three colours. He cannot paint two adjacent surfaces the same colour. He decides to use red, white and green. How many different ways can he paint his room?
(A) 2
(B) 3
(C) 6
(D) 12
(E) 24
Here is a list of fractions which, when written in simplest form, have a denominator less than 6 :
\[\frac{1}{5}, \square, \frac{1}{3}, \frac{2}{5}, \square, \square, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}\]
The list is in ascending order, but three fractions are omitted. The sum of these three fractions is
(A) 1
(B) 2
(C) \(\frac{21}{20}\)
(D) \(\frac{27}{20}\)
(E) \(\frac{29}{20}\)
In autumn, Tilly's meadow changes rapidly with the weather.
The number of flowering plants starts at 150000 but they are dying off so each week the number halves. At the same time, the number of fungi starts at 20 and triples each week.
To the nearest week, how long will it be until the fungi outnumber the flowering plants?
(A) 3 weeks
(B) 5 weeks
(C) 8 weeks
(D) 11 weeks
(E) 13 weeks
A formula in physics is given as:
\(
r=\frac{m V}{q B}
\)
If (q) was trebled, \(m\) was halved and \(r\) and \(B\) remained the same, then \(V\) would
(A) increase by a factor of 6
(B) decrease by a factor of 5
(C) stay the same
(D) double
(E) increase by a factor of 3
In this diagram, \(A D=12\) and \(A B C\) and \(C D E\) are right-angled isosceles triangles. The area of triangle \(B D E\) is 9 . What is the area of triangle \(A B D\) ?
(A) 36
(B) 50
(C) 54
(D) 60
(E) 72
The numbers \(1^{40}, 2^{30}, 3^{20}\) and \(4^{10}\), in increasing order, are
(A) \(1^{40}, 4^{10}, 2^{30}, 3^{20}\)
(B) \(1^{40}, 3^{20}, 4^{10}, 2^{30}\)
(C) \(4^{10}, 3^{20}, 2^{30}, 1^{40}\)
(D) \(1^{40}, 2^{30}, 3^{20}, 4^{10}\)
(E) \(1^{40}, 2^{30}, 4^{10}, 3^{20}\)

In the rectangle \(A B C D\), the lengths marked \(x\), \(y\) and \(z\) are positive integers.
Triangle \(A E D\) has an area of 12 square units and triangle \(B C E\) has an area of 21 square units. How many possible values are there for \(z\) ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

A square is divided into three congruent isosceles triangles and a shaded pentagon, as shown. What fraction of the square's area is shaded?
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{\sqrt{2}}{6}\)
(D) \(\frac{\sqrt{3}}{8}\)
(E) \(2-\sqrt{3}\)
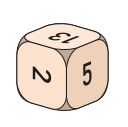
A non-standard dice has the numbers \(2,3,5,8,13\) and 21 on it. The dice is rolled twice and the numbers are added together. What is the probability that the resulting sum is also a value on the dice?
(A) \(\frac{1}{9}\)
(B) \(\frac{5}{12}\)
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{6}\)
(E) \(\frac{2}{9}\)
If \(a\) and \(b\) are positive numbers, then \(\sqrt{a^2+\frac{1}{b^2}} \times \sqrt{b^2+\frac{1}{a^2}} \quad\) is equal to
(A) \(\frac{a}{b}+\frac{b}{a}\)
(B) \(a^2 b^2+\frac{1}{a^2 b^2}\)
(C) \(a b+2+\frac{1}{a b}\)
(D) \(a+b+\frac{1}{a}+\frac{1}{b}\)
(E) \(a b+\frac{1}{a b}\)

The quadrilateral shown is cut into two equal areas by the dashed line.
What is the ratio \(a: b\) ?
(A) \(2: 1\)
(B) \(7: 3\)
(C) \(5: 2\)
(D) \(4: 3\)
(E) \(3: 2\)
Positive integers \(x\) and \(y\) satisfy the equation\[x^2+2 x y+2 y^2+2 y=1988\]What is the largest possible value of \(x+y\) ?
(A) 33
(B) 38
(C) 42
(D) 46
(E) 47

What fraction of the area of the diagram is shaded?
(A) \(\frac{1}{4}\)
(B) \(\frac{4}{9}\)
(C) \(\frac{5}{12}\)
(D) \(\frac{1}{2}\)
(E) \(\frac{5}{18}\)
Sebastien is playing with a square paper serviette with side length 24 centimetres. He folds it in half along a diagonal to obtain a triangle \(A B C\) with a right angle at \(A\). He then folds the triangle so that \(C\) ends up on line \(A B\) at some point \(D\). Suppose that the fold created meets \(B C\) at the point \(X\). Sebastien then folds \(B\) to meet \(X\) and notices that the fold created passes through the point \(D\). The distance in centimetres between the points \(A\) and \(D\) is
(A) \(6 \sqrt{2}\)
(B) \(12(\sqrt{3}-1)\)
(C) 10
(D) 12
(E) \(24(\sqrt{2}-1)\)
The fraction \(\frac{a}{b}\) is positive and in lowest terms, so that \(a\) and \(b\) are positive with no common factors.
When I add the integer \(n\) to both the numerator and denominator of the fraction \(\frac{a}{b}\), the result is double the original fraction.
When I subtract (n) from both the numerator and denominator, the result is triple the original value.
The value of \(n\) is
(A) 13
(B) 18
(C) 21
(D) 24
(E) 28

A cube has an internal point \(P\) such that the perpendicular distances from \(P\) to the six faces of the cube are \(1 \mathrm{~cm}, 2 \mathrm{~cm}, 3 \mathrm{~cm}, 4 \mathrm{~cm}, 5 \mathrm{~cm}\) and 6 cm .
How many other internal points of the cube have this property?
(A) 5
(B) 11
(C) 23
(D) 47
(E) infinitely many
A 70 cm long loop of string is to be arranged into a shape consisting of two adjacent squares, as shown on the left. The side of the smaller square must lie entirely within the side of the larger one, so the example on the right is not allowed.

What is the minimum area of the resulting shape, in square centimetres?
How many pairs \((m, n)\) exist, where \(m\) and \(n\) are different divisors of 2310 and \(n\) divides \(m\) ? Both 1 and 2310 are considered divisors of 2310 .

A grid that measures 20 squares tall and 21 squares wide has each of its squares painted either green or gold. The diagram shows part of the grid, including the top-left corner.
The pattern follows these rules:
How many of the \(20 \times 21=420\) squares are painted green?
Starting with a paper rectangle measuring \(1 \times \sqrt{2}\) metres, Sadako makes a single cut to remove the largest square possible, leaving a rectangle. She repeats this process with the remaining rectangle, producing another square and a smaller rectangle.
Since \(\sqrt{2} \approx 1.41421356\) is irrational, she can in theory keep doing this forever, producing an infinite sequence of paper squares.
To the nearest centimetre, what would be the total perimeter of this infinite pile of squares?
An elastic band is wound around a deck of playing cards three times so that three horizontal stripes are formed on the top of the deck, as shown on the left. Ignoring the different ways the rubber band could overlap itself, there are essentially two different patterns it could make on the under side of the deck, as shown on the right.
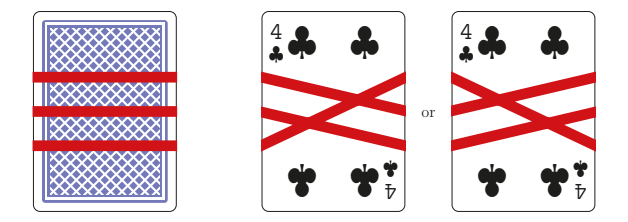
Treating two patterns as the same if one is a \(180^{\circ}\) rotation of the other, how many different patterns are possible on the under side of the deck if the rubber band is wound around to form seven horizontal stripes on top?