Australian Mathematics Competition - 2021- Middle Primary Division - Question
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesHow many dots are on this domino?

(A) 5
(B) 7
(C) 9
(D) 10
(E) 11
What is the difference between 14 and 2?
(A) 28
(B) 16
(C) 12
(D) 10
(E) 7
This Nigerian flag is white and green. What fraction of it is green?

(A) one-third
(B) one-quarter
(C) one-half
(D) two-fifths
(E) two-thirds
[234+100=]
(A) 23400
(B) 1234
(C) 120304
(D) 334
(E) 244
How many minutes are in a quarter of an hour?
(A) 4
(B) 10
(C) 15
(D) 20
(E) 4
My tank can hold \(80 \mathrm{~kL}\) of water. The indicator on the tank shows the water level inside the tank.
Which of the following is closest to the amount of water in the tank?

(A) \(35 \mathrm{~kL}\)
(B) \(45 \mathrm{~kL}\)
(C) \(55 \mathrm{~kL}\)
(D) \(65 \mathrm{~kL}\)
(E) \(75 \mathrm{~kL}\)
Which number makes this number sentence true?

(A) 0
(B) 4
(C) 12
(D) 9
(E) 14
Each face of this cube is divided into 4 small squares. How many small squares are there on the outside of the cube altogether?

(A) 16
(B) 18
(C) 20
(D) 24
(E) 30
A cross country track is marked out with a number of flags as shown.
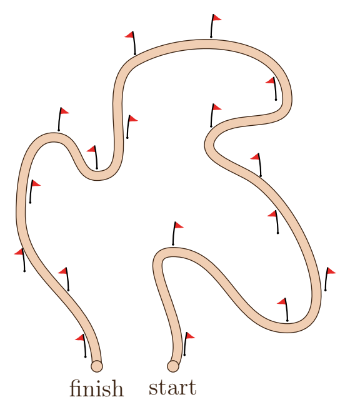
How many of the flags will be on the left of the runners when they pass them?
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11
Which one of these shaded areas is the largest?

Leo is waiting in line at school. There are four students ahead of him and twice as many behind him. How many students are in this line?
(A) 4
(B) 8
(C) 9
(D) 12
(E) 13
I am shuffling a deck of cards but I accidentally drop a card on the ground every now and then. After a while, I notice that I have dropped five cards.

From above, the five cards look like one of the following pictures. Which picture could it be?
Kayla had six apples. She cut them all into quarters and shared them equally between her three brothers and herself. How many apples do they each receive?
(A) 1
(B) 3
(C) \(1 \frac{1}{4}\)
(D) \(1 \frac{1}{3}\)
(E) \(1 \frac{1}{2}\)
Five boxes are compared on a balance.

Which of the five boxes is lightest?

Lydia is saving for a cricket bat. The sports shop has the bat she wants for \(\$ 56\) and her grandfather has promised to pay half the price. She has saved \(\$ 16\). How much more does she need to save before she can buy the bat?
(A) \(\$ 4\)
(B) \(\$ 12\)
(C) \(\$ 20\)
(D) \(\$ 28\)
(E) \(\$ 36\)
Five cards with digits (1,2,2,3,4) and 9 are arranged to form the largest possible 5-digit even number. Which digit is in the tens place?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 9
Each letter in this grid stands for a number from 1 to 6 . The numbers outside the grid are the sums of the values of all the letters in each row or column. For example, in the first column, the values of (M, L, L) and (R) add to 16 . What is the value of the letter (L) ?

(A) 1
(B) 2
(C) 3
(D) 5
(E) 6
Greg is 19 years old, Karin is 26 and Anthony is 31. In how many years from now will their ages add to 100 ?
(A) 6
(B) 8
(C) 16
(D) 24
(E) 26
Mr Northrop's class has students from Ainslie, Turner, Downer, Watson and Dickson. He made a chart showing how many live in each suburb.

Unfortunately his dog tore the bottom of the chart, leaving only the last few letters of each suburb. He forgot the order of the suburbs on the chart, but he remembered that more students live in Downer than Watson.
How many students live in Turner?
(A) 3
(B) 5
(C) 6
Alexander's pen leaked on his addition homework, covering up three of the digits in the calculation shown. How many different possibilities are there for the correct working?

(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Here are four sentences and their translations into Windarian, an invented language. The two lists are not in the same order.

How should we translate the sentence 'Mum loves oranges'?
(A) Awe tum kete
(B) Ato bem kito
(C) Eke tum kito
(D) Awe bem kete
(E) Eke bem kito
The biscuit section in a cookbook has 6 pages. The sum of all the page numbers in this section is 147 . What is the number of the last page in this section of the book?
(A) 26
(B) 27
(C) 28
(D) 29
(E) 30
Six white cubes are joined together as shown. The model is then painted blue all over.
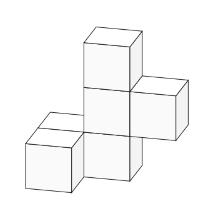
When the model is pulled apart, how many faces of these cubes are still white?
(A) 4
(B) 5
(C) 8
(D) 10
(E) 13
Three gears are connected as shown. The two larger gears have 20 teeth each and the smaller gear has 10 teeth.

The middle gear is rotated half a turn in the direction of the arrows, turning the \(\mathrm{M}\) upside down.
What do the three gears look like after this rotation?

In a dice game, Yasmin rolls 5 standard dice, all at once.
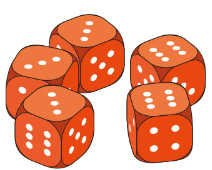
She needs to roll a full house, which has a triple of one number and a pair of a different number. How many different full house rolls are possible?
(A) 2
(B) 5
(C) 18
(D) 25
(E) 30
This is a magic square, so that all rows, columns and diagonals add up to the same sum. Some numbers are already filled in.

When we complete it and multiply the numbers in the three shaded squares, what do we get?
Hayden saved \(\$ 1420\) and Mitchell saved \(\$ 505\). After they each spent an equal amount of money, Hayden had 4 times as much money as Mitchell. In dollars, how much did each of them spend?
The block pattern below has 1 block in the first tower, 4 blocks in the second tower, 9 blocks in the third tower and so on. How many blocks are needed to make all of the first ten towers in this pattern?

Verity has 6 cards with digits (1,2,3,4,5) and 6 . She arranges them to form three 2-digit numbers. Only her first number is a multiple of 4 . Only her second number is a multiple of 5. Only her third number is a multiple of 6. What is the answer when she multiplies her first two numbers and then adds her third number?

I want to place the numbers 1 to 10 in this diagram, with one number in each circle. On each of the three sides, the four numbers add to a side total, and the three side totals are all the same.

What is the smallest number that this side total could be?