Australian Mathematics Competition - 2021- Junior years - Grade 7 & 8 - Questions and Solutions

Problem 1:

\(2021-1202=\)

(A) 719
(B) 723
(C) 819
(D) 823
(E) 3223

Problem 2:

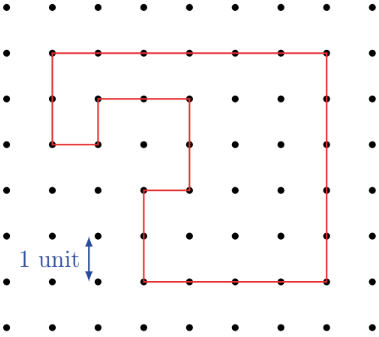
What is the perimeter of this figure?

(A) 28 units
(B) 26 units
(C) 24 units
(D) 20 units
(E) 21 units

Problem 3:

The area of this triangle is

(A) \(10\) \(cm^2\)
(B) \(12\) \(cm^2\)
(C) \(12.5\) \(cm^2\)
(D) \(15\) \(cm^2\)
(E) \(16\) \(cm^2\)

Problem 4:

On the number line below, the fraction \(\frac{3}{8}\) lies between

(A) (P) and (Q)
(B) (Q) and (R)
(C) (R) and (S)
(D) (S) and (T)
(E) (T) and (U)

Problem 5:

Which of the following is closest to \(2021\)?

(A) \(202 \times 100\)
(B) \(22 \times 1000\)
(C) \(20.2 \times 100\)
(D) \(10 \times 20.2\)
(E) \(100 \times 2.2\)

Problem 6:

In the diagram, \(AB\) is parallel to \(EF\) and \(DE\) is parallel to \(BC\). What is the value of \(x\)?

(A) 43
(B) 47
(C) 133
(D) 135
(E) 137

Problem 7:

Mister Meow attempted the calculation \(5\times 2 + 4\), but accidentally swapped the multiplication and addition symbols. His answer was

(A) too low by 2
(B) too low by 1
(C) still correct
(D) too high by 1
(E) too high by 2

Problem 8:

Dad puts a cake in the oven at 11:49 am. The recipe says to bake it for 75 minutes. When should the cake come out of the oven?

(A) 1:04 pm
(B) \(12: 34 \mathrm{pm}\)
(C) \(1: 54 \mathrm{pm}\)
(D) 1:19 pm
(E) \(12: 04 \mathrm{pm}\)

Problem 9:

Damon made up a joke and texted it to three people in his class. These three each texted it to three other people in the class. No one receiving the joke had seen it before. Including Damon, how many people now know the joke?

(A) 9
(B) 11
(C) 13
(D) 15
(E) 16

Problem 10:

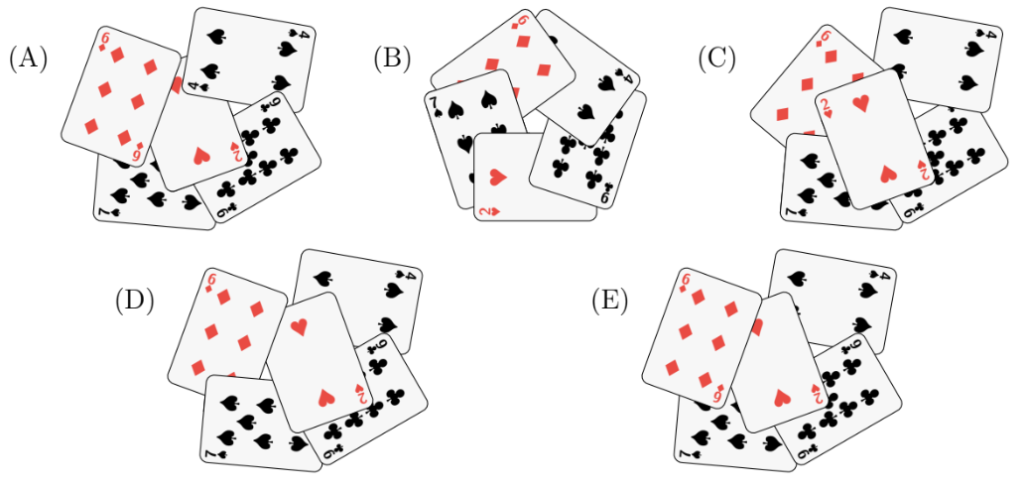
I am shuffling a deck of cards but I accidentally drop a card on the ground now and then. After a while, I notice that I have dropped five cards. From above, the five cards look like one of the following pictures. Which picture could it be?

Problem 11:

To feed a horse, Kim mixes three bags of oats with one bag containing 20% lucerne and 80% oats. If all the bags have the same volume, what percentage of the combined feed mixture is lucerne?

(A) 3
(B) 5
(C) 6
(D) 20
(E) 60

Problem 12:

Three squares with perimeters 12 cm, 20 cm and 16 cm are joined as shown. What is the perimeter of the shape formed?

(A) 34 cm
(B) 40 cm
(C) 41 cm
(D) 42 cm
(E) 48 cm

Problem 13:

The odometer in my car measures the total distance travelled. At the moment, it reads 199 786 kilometres. I’m interested in when the odometer reading is a palindrome so that it reads the same backwards as forwards. How many more kilometres of travel will this take?

(A) 25
(B) 125
(C) 15
(D) 205
(E) 2005

Problem 14:

A square has an internal point P such that the perpendicular distances from P to the four sides are 1 cm, 2 cm, 3 cm, and 4 cm. How many other internal points of the square have this property?

(A) 1
(B) 3
(C) 5
(D) 7
(E) 9

Problem 15:

How many different positive whole numbers can replace the \(\triangle\) to make this a true statement?

\([
\frac{\triangle}{10}+\frac{1}{3}<1
]\)

Problem 16:

Three blocks with rectangular faces are placed together to form a larger rectangular prism. All blocks have side lengths which are whole numbers of centimetres. The areas of some of the faces are shown, as is the length of one edge. In cubic centimetres, what is the volume of the combined prism?

(A) 360
(B) 540
(C) 600
(D) 720
(E) 900

Problem 17:

I have four consecutive odd numbers. The largest is one less than twice the smallest. Which of the following is the largest of the four numbers?

(A) 9
(B) 11
(C) 13
(D) 15
(E) 21

Problem 18:

This is a square with sides of 10 metres. From the constructions shown, which of the areas is the largest?

(A) (A)
(B) (B)
(C) (C)
(D) (D)
(E) (E)

Problem 19:

Sandy, Rachel and Thandie collect toy cars. Altogether they have 300 cars. Rachel has grown up and decides to give her cars away. If she gives them all to Sandy, then Sandy will have 180. If she gives
them all to Thandie, then Thandie will have 200. How many cars does Rachel have?

(A) 80
(B) 90
(C) 100
(D) 110
(E) 120

Problem 20:

A standard dice numbered 1 to 6 with opposite sides adding to 7 is placed on a 2 by 2 square as shown. The dice is rolled over one edge onto each of the four base squares in turn and then back on to the original square, as indicated by the arrows. Which side of the dice is now facing upwards?

Problem 21:

Leonhard is designing a puzzle for Katharina. It has nine squares in a \(3 \times 3\) grid and several clues. Each clue is a number 1,2 or 3 placed in one of the squares. Katharina then has to find a solution by placing 1,2 or 3 in each of the remaining squares so that no row or column has a repeated number.
What is the smallest number of clues that Leonhard could include so that his puzzle has exactly one solution?

(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 22:

Grandma and Grandpa took their three grandchildren to the cinema. They purchased 5 seats in a row. Each grandparent wanted to sit next to two of the grandchildren. How many such seating arrangements are possible?

(A) 8
(B) 12
(C) 30
(D) 3
(E) 60

Problem 23:

I have a 4 by 4 by 4 cube made up of 64 unit cubes. I paint 3 faces of the larger cube. Then I pull the cube apart. Which of the following could be the number of unit cubes with no paint on them?

(A) 16
(B) 21
(C) 24
(D) 28
(E) 36

Problem 24:

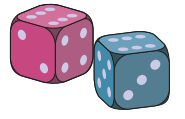
Ben and Jerry each roll a standard dice. If Ben rolls higher than Jerry, he wins; otherwise,e Jerry wins. What is the probability that Ben wins?

(A) \(\frac{1}{6}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{5}{12}\)
(D) \(\frac{17}{36}\)
(E) \(\frac{1}{2}\)

Problem 25:

In the diagram, \(\triangle P Q R\) is isosceles, with \(P Q=Q R . S\) is a point on \(P R\) and \(T\) is a point on \(P Q\) such that \(Q T=Q S\), and \(\angle S Q R=20^{\circ}\). The size of \(\angle T S P\), in degrees, is

(A) 10
(B) 12
(C) 15
(D) 20
(E) 24

Problem 26:

Starting with a 43 × 47 rectangle of paper, Sadako cuts the paper to remove the largest square possible. With the remaining rectangle, she again cuts it to remove the largest square possible. She continues doing this until the remaining piece is a square. What is the total perimeter of all the squares Sadako has at the end?

Problem 27:

There are 14 chairs equally spaced around a circular table, and numbered from 1 up to 14. How many ways are there to choose two chairs that are not opposite each other?

Problem 28:

A swimming medley consists of 100 metres of each butterfly, backstroke, breaststroke and freestyle, in that order. I swim freestyle 3 times faster than breaststroke, and butterfly twice as fast as breaststroke, and my backstroke is half as fast as my freestyle. It takes me 6 minutes to swim the full medley. To the nearest metre, how far will I have swum after 4 minutes?

Problem 29:

An ant’s walk starts at the apex of a regular octahedron as shown. It walks along edges, never retracing its path. It visits each of the other five vertices exactly once. In how many different ways can the ant do this?

Problem 30:

Consider a \(15 \times 15\) grid of unit squares. In the square in row \(a\) and column \(b\), we write the number \(a \times b\). We then colour the squares black and white in a checkerboard fashion, so that the square labelled 225 is coloured white. The diagram shows the parts of the grid near each corner. What are the last three digits of the sum of the numbers in the white squares?