Australian Mathematics Competition - 2020 - Junior years - Grade 7 & 8 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
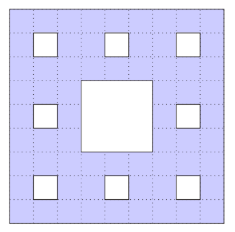
Join Trial or Access Free ResourcesHow many \(1 \times 1\) squares are in this diagram?

(A) 16
(B) 18
(C) 20
(D) 24
(E) 25
What is half of 2020?
(A) 20
(B) 101
(C) 110
(D) 1001
(E) 1010
What is the perimeter of this triangle?
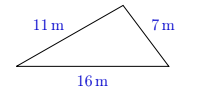
(A) 33 m
(B) 34 m
(C) 35 m
(D) 36 m
(E) 37 m
I stepped on the train at 8.48 am and left at 9.21 am. How many minutes did I spend on the train?
(A) 27
(B) 33
(C) 43
(D) 87
(E) 93
What is the value of \(y\) in this triangle?

(A) 10
(B) 30
(C) 50
(D) 70
(E) 90
\(2-(0-(2-0))\)=
(A) -4
(B) -2
(C) 0
(D) 2
(E) 4
In the grid, the total of each row is given at the end of the row, and the total of each column is given at the bottom of the column.
The value of \(N\) is

(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
A letter \(\mathbf{G}\) is rotated clockwise by \(135^{\circ}\). Which of the following pictures best represents the final image?

\(\frac{1+2+3+4+5}{1+2+3+4}-\frac{1+2}{1+2+3}=\)
(A) 3
(B) \(\frac{5}{6}\)
(C) 1
(D) \(\frac{7}{6}\)
(E) 2
Sebastien is thinking of two numbers whose sum is 26 and whose difference is 14 . The product of Sebastien's two numbers is
(A) 80
(B) 96
(C) 105
(D) 120
(E) 132
A country consists of two islands as shown on this map. In square kilometres, its area is

(A) between 100 and 1000
(B) between 1000 and 10000
(C) between 10000 and 100000
(D) between 100000 and 1000000
(E) greater than 1000000
\(123456-12345+1234-123+12-1=\)
(A) 33333
(B) 101010
(C) 111111
(D) 122223
(E) 112233
Lily is 2020 days old. How old was she on her last birthday?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8
A piece of paper is folded twice as shown and cut along the dotted lines. Once unfolded, which letter does the piece of paper most resemble?

(A) M
(B) O
(C) N
(D) B
(E) V
An equilateral triangle is subdivided into several smaller equilateral triangles, as shown. The shaded triangle has a side length of 2. What is the perimeter of the large triangle?

(A) 24
(B) 27
(C) 30
(D) 33
(E) 36
The \(\triangle (X Y S)\) is enclosed by a rectangle \(P Q R S\) as shown in the diagram. In square centimetres, what is the area of \(\triangle (X Y S)\)?

(A) 82
(B) 88
(C) 94
(D) 112
(E) 130
Four teams play in a soccer tournament. Each team plays one game against each of the other three teams. Teams earn 3 points for a win, 1 point for a draw and 0 points for a loss. After all the games have been played, one team has 6 points, two teams have 4 points and one team has 3 points. How many games ended in a draw?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
An isosceles triangle has a perimeter of 28 cm and sides of integer length. How many different such triangles can be made?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
In the grid shown, the numbers from 1 to 4 must appear once in each row and column. Also, the sum of numbers in each of the four regions separated by red lines must be the same. What is the sum (x+y) ?

(A) 8
(B) 7
(C) 6
(D) 5
(E) 4
Anupam has a cardboard square with a perimeter of 400 centimetres. He draws a horizontal line and a vertical line on the square and cuts along these lines to create four rectangles. What is the largest possible sum of the perimeters of these four rectangles, in centimetres?
(A) 400
(B) 600
(C) 800
(D) 1000
(E) 1200
The ends of the tangled string shown are pulled in the direction of the arrows so that the string either untangles or forms a simpler knot.

Which of the following best matches the knot, or otherwise, that is formed when the string is tightened?

Mr Atkins wrote some homework questions for his class to practise order of operations. One of the questions was \(2+3 \times(4+3)\), with answer 23 . However, one of his students just worked from left to right and ignored the brackets, writing \(2+3=5\), \(5 \times 4=20,20+3=23\), the correct answer. Mr Atkins thought that this was fascinating, so he tried to come up with another question where working left to right gave the right answer. He tried \(5+4 \times(7+\square)\). What number should he put in the box?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
My friend and I took a maths test with 10 questions. Question 1 was worth 1 mark, question 2 was worth 2 marks, question 3 was worth 3 marks, and so on. Correct answers scored full marks and incorrect answers scored 0 marks. We both scored the same number of marks and correctly answered the same number of questions. However, we didn't solve exactly the same set of questions as each other. What is the maximum score that I could have received for the test?
(A) 44
(B) 46
(C) 48
(D) 50
(E) 52
A light rail network has 21 drivers, but not all of them are required at the same time:
Given that every driver must work on at least one of these shifts, what is the maximum number of drivers that can work on all three shifts?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
A bag contains exactly 50 coins. The coins are either worth 10 cents, 20 cents or 50 cents, and there is at least one of each. The total value of the coins is (\$ 10). How many different ways can this occur?
(A) 2
(B) 4
(C) 8
(D) 12
(E) 16
The digits 1 to 9 are used exactly once each to make three 3-digit numbers. The second number is three times the first number. The third number is five times the first number. What is the second number?
Madeleine types her three-digit Personal Identification Number (PIN) into this keypad. All three digits are different, but the buttons for the first and second digits share an edge, and the buttons for the second and third digits share an edge. For instance, 563 is a possible PIN, but 536 is not, since 5 and 3 do not share an edge. How many possibilities are there for Madeleine's PIN?

Starting with a \(9 \times 9 \times 9\) cube, Augusta removed as few \(1 \times 1 \times 1\) cubes as possible so that the resulting sculpture had front view, top view and side view all the same, as shown. How many \(1 \times 1 \times 1\) cubes did Augusta remove?
A different integer from 1 to 10 is placed on each of the faces of a cube. Each vertex is then assigned a number which is the sum of the numbers on the three faces which touch that vertex. Only the vertex numbers are shown here. What is the product of the 4 smallest face numbers?

My grandson makes wall hangings by stitching together 16 square patches of fabric into a \(4 \times 4\) grid. I asked him to use patches of red, blue, green and yellow, but to ensure that no patch touches another of the same colour, not even diagonally. The picture shows an attempt which fails only because two yellow patches touch diagonally. In how many different ways can my grandson choose to arrange the coloured patches correctly?
