Australian Mathematics Competition - 2019 - Senior years 11 -12 Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat is the value of \(201 \times 9\)?
(A) 189
(B) 1809
(C) 1818
(D) 2001
(E) 2019
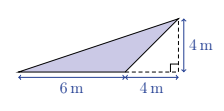
What is the area of the shaded triangle?
(A) \(8 \mathrm{~m}^2\)
(B) \(12 \mathrm{~m}^2\)
(C) \(14 \mathrm{~m}^2\)
(D) \(20 \mathrm{~m}^2\)
(E) \(24 \mathrm{~m}^2\)
What is \(19 \%\) of \(\$ 20\)?
(A) \(\$ 20.19\)
(B) \(\$ 1.90\)
(C) \(\$ 0.19\)
(D) \(\$ 3.80\)
(E) \(\$ 0.38\)
What is the value of \(z\)?
(A) 30
(B) 35
(C) 45
(D) 50
(E) 55
The value of \(2^0+1^9\) is
(A) 1
(B) 2
(C) 3
(D) 10
(E) 11
Let \(f(x)=3 x^2-2 x\). Then \(f(-2)=\)
(A) -32
(B) -8
(C) 16
(D) 32
(E) 40

This kite has angles \(\theta, \theta, \theta\) and \(\frac{\theta}{3}\). What is the size of the angle \(\theta\)?
(A) \(120^{\circ}\)
(B) \(105^{\circ}\)
(C) \(90^{\circ}\)
(D) \(112^{\circ}\)
(E) \(108^{\circ}\)
Consider the undulating number sequence
$$
1,4,7,4,1,4,7,4,1,4, \ldots,
$$
which repeats every four terms. The running total of the first 3 terms is 12. The running total of the first 7 terms is 28.
Which one of the following is also a running total of this sequence?
(A) 61
(B) 62
(C) 67
(D) 66
(E) 65
Mia walks at 1.5 metres per second. Her friend Crystal walks at 2 metres per second. They walk in opposite directions around their favourite bush track, starting together from the same point. They first meet again after 20 minutes. How long, in kilometres, is the track?
(A) 3.5
(B) 4.2
(C) 6
(D) 7
(E) 8.4
$$
\frac{1^1+2^2+3^3+4^4}{1^1+2^2+3^3}=
$$
(A) \(2^3\)
(B) \(3^2\)
(C) 11
(D) \(4^3\)
(E) 259
The 5-digit number \(P 679 Q\) is divisible by 72. The digit \(P\) is equal to
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

The altitude of a right-angled triangle divides the hypotenuse into lengths of 4 and 6. What is the area of the triangle?
(A) \(10 \sqrt{6}\)
(B) 24
(C) 25
(D) 12
(E) \(6 \sqrt{10}\)
In a box of apples, \(\frac{3}{7}\) of the apples are red and the rest are green. Five more green apples are added to the box. Now \(\frac{5}{8}\) of the apples are green. How many apples are there now in the box?
(A) 32
(B) 33
(C) 38
(D) 40
(E) 48
Which number exceeds its square by the greatest possible amount?
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{3}{4}\)
(E) \(\frac{\sqrt{2}}{2}\)

A regular nonagram is a nine-pointed star drawn as shown. What is the angle at each of the nine points?
(A) \(100^{\circ}\)
(B) \(110^{\circ}\)
(C) \(120^{\circ}\)
(D) \(130^{\circ}\)
(E) \(140^{\circ}\)
Two sequences are constructed, each with 900 terms:
\(5,8,11,14, \ldots \quad\) increasing by 3
\(3,7,11,15, \ldots \quad\) increasing by 4
How many terms do these two sequences have in common?
(A) 400
(B) 300
(C) 275
(D) 225
(E) 75

A circular steel gateway surrounding a rectangular gate is designed as shown. The total height of the gateway is divided into 10 equal intervals by equally-spaced horizontal bars.
The rectangular gate is what fraction of the area of the entire circular gateway?
(A) \(\frac{48}{25 \pi}\)
(B) \(\frac{\sqrt{3}}{\pi}\)
(C) \(\frac{2}{\pi}\)
(D) \(\frac{8 \sqrt{2}}{25 \pi}\)
(E) \(\frac{8}{5 \pi}\)
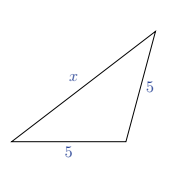
For what values of \(x\) does the triangle with side lengths 5, 5 and \(x\) have an obtuse angle?
(A) \(0<x \leq 5 \sqrt{2}\)
(B) \(5<x \leq 5 \sqrt{2}\)
(C) \(5<x<10\)
(D) \(0<x<10\)
(E) \(5 \sqrt{2}<x<10\)
A rectangle has area 20 and perimeter 22. How long is each of its diagonals?
(A) \(4 \sqrt{5}\)
(B) 10
(C) \(\sqrt{29}\)
(D) \(2 \sqrt{26}\)
(E) 9
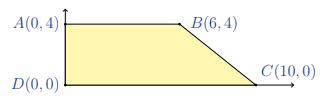
The line \(y=m x\) divides quadrilateral \(A B C D\) into two equal areas.
The value of \(m\) is \(A\) 1
(B) \(\frac{2}{3}\)
(C) \(\frac{8}{17}\)
(D) \(\frac{8}{15}\)
(E) \(\frac{8}{25}\)
Manny has three ways to travel the 8 kilometres from home to work: driving his car takes 12 minutes, riding his bike takes 24 minutes and walking takes 1 hour and 44 minutes. He wants to know how to get to work as quickly as possible in the event that he is riding his bike and gets a flat tyre.
He has three strategies:
(i) If he is close to home, walk back home and then drive his car.
(ii) If he is close to work, just walk the rest of the way.
(iii) For some intermediate distances, spend 20 minutes fixing the tyre and then continue riding his bike.
He knows there are two locations along the route to work where the strategy should change. How far apart are they?
(A) 2 km
(B) 3 km
(C) 4 km
(D) 5 km
(E) 6 km

A circular coin of radius 1 cm rolls around the inside of a square without slipping, always touching the boundary of the square. When it returns to where it started, the coin has performed exactly one whole revolution. In centimetres, what is the side length of the square?
(A) \(\pi\)
(B) 3.5
(C) \(1+\pi\)
(D) 4
(E) \(2+\frac{\pi}{2}\)
A passenger train 200 m long and travelling at \(80 \mathrm{~km} / \mathrm{h}\) passes a goods train 2 km long travelling in the opposite direction at \(20 \mathrm{~km} / \mathrm{h}\). What is the distance, measured along one of the tracks, between the point at which the fronts of the trains pass each other and the point at which their back ends pass each other?
(A) 1.28 km
(B) 1.4 km
(C) 1.56 km
(D) 1.8 km
(E) 1.88 km

A circle \(C\) and a regular hexagon \(H\) have equal area. A regular hexagon \(H^{\prime}\) is inscribed in \(C\), and a circle \(C^{\prime}\) is inscribed in \(H\).
What is the ratio of the area of \(H^{\prime}\) to the area of \(C^{\prime}\) ?
(A) \(1: 1\)
(B) \(3: \pi\)
(C) \(9: \pi^2\)
(D) \(3: 4\)
(E) \(3 \sqrt{3}: 2 \pi\)

A cube of side length 1 is cut into three pieces of equal volume by two planes passing through the diagonal of the top face. One plane cuts the edge \(\overline{U V}\) at the point \(P\). What is the length \(P V\) ?
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{\sqrt{2}}{2}\)
(D) \(\sqrt{3}-1\)
(E) \(\frac{\sqrt{5}-1}{2}\)
The number 35 has the property that when its digits are both increased by 2 , and then multiplied, the result is \(5 \times 7=35\), equal to the original number.
Find the sum of all two-digit numbers such that when you increase both digits by 2 , and then multiply these numbers, the product is equal to the original number.
In a list of numbers, an odd-sum triple is a group of three numbers in a row that add to an odd number. For instance, if we write the numbers from 1 to 6 in this order,
6
4
2
1
3
5
then there are exactly two odd-sum triples: \((4,2,1)\) and \((1,3,5)\).
What is the greatest number of odd-sum triples that can be made by writing the numbers from 1 to 1000 in some order?
Terry has a solid shape that has four triangular faces. Three of these faces are at right angles to each other, while the fourth face has side lengths 11,20 and 21 . What is the volume of the solid shape?
The diagram shows one way in which a \(3 \times 10\) rectangle can be tiled by 15 rectangles of size \(1 \times 2\).
Since this tiling has no symmetry, we count rotations and reflections of this tiling as different tilings. How many different tilings of this \(3 \times 10\) rectangle are possible?

A function (f), defined on the set of positive integers, has \(f(1)=2\) and \(f(2)=3\). Also \(f(f(f(n)))=n+2\) if \(n\) is even and \(f(f(f(n)))=n+4\) if \(n\) is odd. What is \(f(777) \)?