Australian Mathematics Competition - 2014 - Upper Primary - Grade 5 & 6 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat is the value of \(7+6+4+3\) ?
(A) 20
(B) 19
(C) 18
(D) 17
(E) 16
Which shape can make a pyramid if you fold along the dotted lines?

A square of paper is folded in half to make a triangle, then in half to make a smaller triangle, then in half again to make an even smaller triangle.
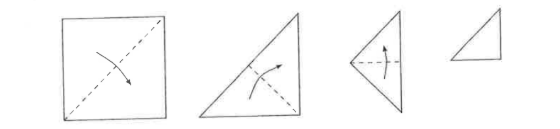
How many layers of paper are in the final triangle?
(A) 3
(B) 4
(C) 6
(D) 8
(E) 12
The year 5 students at my local school were surveyed to find which one of the four teams in the local football competition they followed.

How many more students followed the most popular team than followed the least popular team?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 8
This week at my lemonade stand I sold \(\$ 29\) worth of lemonade, but I had spent \(\$ 34\) on lemons and \(\$ 14\) on sugar. My total loss for the week was
(A) \(\$ 1\)
(B) \(\$ 9\)
(C) \(\$ 19\)
(D) \(\$ 21\)
(E) \(\$ 29\)

A piece of paper is cut out and labelled as shown. It is folded along the dashed lines to form an open box and placed so that the top is open. Which letter is on the bottom of the box?
(A) A
(B) B
(C) C
(D) D
(E) E
Which of the following gives an odd number?
(A) \(12^2\)
(B) \(141-57\)
(C) \(36 \times 9\)
(D) \(308 \div 7\)
(E) \(\frac{1}{3}\) of 123
A new block of flats is being built and Trudy is buying the letterbox numbers. The letterboxes are to be labelled from 190 to 212 . How many zeros will she need to buy?
(A) 22
(B) 13
(C) 12
(D) 10
(E) 4
This \(4 \times 4\) square grid can be covered by three shapes made from \(1 \times 1\) squares. None of the shapes overlap.

If two of the shapes are

then the third shape is

Given that \(\frac{1001}{77}=13\), what is the value of \(\frac{100.1}{770} ?\)
(A) 0.13
(B) 1.3
(C) 13
(D) 130
(E) 1300

These two squares, each with a side length of 10 cm , overlap as shown in the diagram. The shape of the overlap is also a square which has an area of 16 square centimetres. In centimetres, what is the perimeter of the combined shape?
(A) 40
(B) 56
(C) 64
(D) 80
(E) 92

Six boys looked in the fridge and found this much leftover pizza. They shared the leftover pizza equally. How much of the whole pizza did each boy get?
(A) \(\frac{1}{12}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{1}{6}\)
(D) \(\frac{1}{4}\)
(E) \(\frac{1}{3}\)
Which of the shaded areas below is the largest?

(A) A
(B) B
(C) C
(D) D
(E) E
A map, 40 cm wide and 20 cm high, is folded along the dashed lines indicated to form a \(10 \mathrm{~cm} \times 10 \mathrm{~cm}\) square so that it just fits in its envelope. It is then pinned to a notice board.

Which one of the following could be the pattern of pinholes on the map?

Sally thinks of a number, multiplies it by 2 , adds 2 , divides by 2 and then subtracts 2 . Her answer is 2 . What was her original number?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
The paint colour 'Roebourne Red' is made by mixing 2 parts yellow, 5 parts red and 1 part black.
If a batch of paint was made using 3 litres of yellow, how many litres of paint would be in the whole batch?
(A) 6
(B) 8
(C) 9
(D) 10 ,
(E) 12
A square of paper has its corners folded in as shown to make a smaller square with an internal square, as shown on the right. What is the area of this internal square?
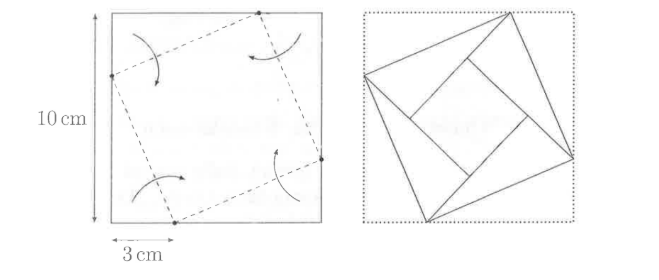
(A) \(4 \mathrm{~cm}^2\)
(B) \(9 \mathrm{~cm}^2\)
(C) \(16 \mathrm{~cm}^2\)
(D) \(49 \mathrm{~cm}^2\)
(E) \(58 \mathrm{~cm}^2\)
Ancient Egyptian mathematicians used fractions but only with a numerator of 1 , such as \(\frac{1}{2}\) or \(\frac{1}{7}\) or \(\frac{1}{14}\). They made other fractions by adding these fractions together. For example, \(\frac{3}{4}\) was written as \(\frac{1}{2}+\frac{1}{4}\). Which of the following is an Ancient Egyptian way of writing \(\frac{11}{16}\) ?
(A) \(\frac{1}{2}+\frac{1}{4}+\frac{1}{10}\)
(B) \(\frac{1}{2}+\frac{1}{8}+\frac{1}{16}\)
(C) \(\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\)
(D) \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\)
(E) \(\frac{1}{3}+\frac{1}{6}+\frac{1}{2}\)

This symmetrical star is made up of two overlapping equilateral triangles of the same size. The area of the star is 60 square centimetres. What is the area of the shaded region in square centimetres?
(A) 30
(B) 36
(C) 42
(D) 45
(E) 48

In this correctly worked addition, \(P, Q, R\) and \(S\) represent different digits, and all seven digits are different. What is the sum of \(P, Q, R\) and \(S\) ?
(A) 23
(B) 22
(C) 18
(D) 16
(E) 14
In a competition between four people, Sally scored twice as many points as Brian and 30 points more than Corrie. Donna scored 50 points more than Brian. Which of the following statements is definitely true?
(A) Sally won the competition.
(B) Brian came last in the competition.
(C) Donna won the competition.
(D) Corrie beat Brian.
(E) Sally and Donna together scored more than Brian and Corrie.
A plane was travelling at an altitude of 4500 metres for 20 minutes. It then climbed at a rate of 500 metres per minute for 5 minutes before descending at 350 metres per minute for 8 minutes. Which of the following graphs best describes the altitude of the plane over this time?

Mrs Graham wants to fill her swimming pool for the summer. She knows that if she uses the backyard hose it will take 12 hours, or if she uses the frontyard hose it will take 4 hours. How long will it take if she uses both hoses together?
(A) 3 hours
(B) 2.5 hours
(C) 2 hours
(D) 1.5 hours
(E) 1 hour
Four soccer teams played each other four times in a season of competition. Each winning team was awarded 3 points. Teams that had a draw were awarded 1 point each, and losing teams were awarded no points. The season ended with Kangaroos on 21 points, Kookaburras on 17 points, Koalas on 16 points and Crocodiles on 12 points. How many games ended in a draw?
(A) 7
(B) 6
(C) 5
(D) 4
(E) 3
Five different whole numbers, chosen from the numbers from 1 to 30 , add up to 30 . What is the greatest possible value of the largest of these numbers?
(A) 6
(B) 10
(C) 15
(D) 20
(E) 26

A 3 by 5 grid of dots is set out as shown. How many straight line segments can be drawn that join two of these dots and pass through exactly one other dot?

A cube is made up of \(1 \mathrm{~cm} \times 1 \mathrm{~cm} \times 1 \mathrm{~cm}\) blocks and measures \(12 \mathrm{~cm} \times 12 \mathrm{~cm} \times 12 \mathrm{~cm}\). Sharyn is using the same set of blocks to make a set of stairs.
The picture shows how she started, making a set of stairs 4 blocks high, 4 blocks from front to back and 5 blocks wide.
Her finished set of stairs will use all the blocks and be 8 blocks high and 8 blocks from front to back. How many blocks wide will they be?
Three whole numbers add up to 149 and multiply to give 987 . What is the largest of the three numbers?
Which three-digit number is 11 times the sum of its digits?
How many three-digit numbers are there in which one of the digits is the sum of the other two?