Australian Mathematics Competition - 2011 - Upper Primary - Grade 5 & 6 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhich of the following numbers has the same value as 152 hundredths?
(A) 1520
(B) 152
(C) 15.2
(D) 1.52
(E) 0.152
The value of \(1+10+10 \times 10+10 \times 10 \times 10\) is
(A) 1010
(B) 10111
(C) 1111
(D) 1110
(E) 11111
Mike buys a can of 5 tennis balls for \(\$ 2.50\). How much would three balls cost?
(A) 90 c
(B) \(\$ 1.50\)
(C) \(\$ 1.80\)
(D) \(\$ 2.40\)
(E) \(\$ 3\)
Auckland's time zone is two hours ahead of Melbourne's. What time is it in Auckland when it is 2 am in Melbourne?
(A) 4 am
(B) midnight
(C) 6 pm
(D) 6 am
(E) 8 am
How many rectangles of any size are in this diagram?

(A) 11
(B) 10
(C) 9
(D) 8
(E) 6
School shirts are on sale for \(25 \%\) off the usual price. Bethany buys a shirt on sale for \(\$ 6.00\). How much did she save?
(A) \(\$ 4.50\)
(B) \(\$ 2.00\)
(C) \(\$ 1.50\)
(D) \(\$ 3.00\)
(E) \(\$ 4.00\)
Which of the following is not a net for an open top box?

Which of the following is true?
(A) If you add two odd numbers you always get an odd number.
(B) If you multiply two odd numbers you always get an even number.
(C) If you add an odd and an even number you always get an even number.
(D) If you multiply an odd and an even number you always get an even number.
(E) If you multiply two even numbers you always get an odd number.
The temperature on a winter's day was recorded in degrees Celsius every hour from 7 am to 12 noon as shown on the graph.

What was the difference, in degrees Celsius, between the temperature recorded at 9 am and at 11 am ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
A notice in an elevator states that 13 persons or 1000 kg is the maximum load. Which of the following is the closest to the average body mass that the manufacturer used for one person?
(A) 13 kg
(B) 50 kg
(C) 80 kg
(D) 100 kg
(E) 130 kg
On weekends, Fred earns money by washing cars and mowing lawns. He receives \(\$ 5\) for a mow and \(\$ 9\) for a car wash. Last weekend he earned \(\$ 56\). Which of the following explanations is possible?
(A) 5 mows and 3 car washes
(B) 6 mows and 3 car washes
(C) 2 mows and 5 car washes
(D) 5 mows and 4 car washes
(E) 4 mows and 4 car washes
The diagram shows a 7-piece tangram puzzle.

What is the area, in square centimetres, of the shaded part if the whole puzzle is a square with side 8 cm ?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
Jennifer has made this hexagonal spinner.

If she spins it 72 times, about how many times would she expect to land on a 2 ?
(A) 6
(B) 8
(C) 10
(D) 12
(E) 24
You are standing somewhere on the map below.

Directly to the east you see a house \(全\), directly to the north you see a person \(\$\) and directly west you can see a tree \(\$\). Which square are you standing in?
(A) D4
(B) F2
(C) J6
(D) G10
(E) J10
Jim is running a two-lap race. He passes a marker on the first lap which is exactly a third of the way round the lap. What fraction of the race will be completed when he passes the same marker again?
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{3}{4}\)
(E) \(\frac{5}{6}\)
Bill is 2 years older than his brother Graham, who in turn is 3 years older than their twin sisters Sally and Jill. If the combined total of their ages is 40 , how old is Graham?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 13
Sam draws a rectangle with sides of length 56 cm and 98 cm . Jan divides Sam's rectangle into squares by drawing lines joining opposite sides. What is the smallest number of lines that Jan must draw?
(A) 9
(B) 10
(C) 11
(D) 13
(E) 15
The areas of three faces of a rectangular prism are 12 square centimetres, 15 square centimetres and 20 square centimetres. What is the volume, in cubic centimetres, of the rectangular prism?
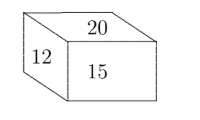
(A) 30
(B) 48
(C) 56
(D) 60
(E) 72
Tony has an 8 cm by 12 cm paper rectangle. He folds it in half three times, each time making a smaller rectangle. What is the smallest possible perimeter of the rectangle after the third fold?
(A) 24 cm
(B) 16 cm
(C) 14 cm
(D) 12 cm
(E) 10 cm
The numbers on the six faces of this cube are consecutive even numbers.

If the sums of the numbers on each of the three pairs of opposite faces are equal, find the sum of all six numbers on this cube.
(A) 196
(B) 188
(C) 210
(D) 186
(E) 198
In the following addition, some of the digits are missing.
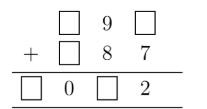
The sum of the missing digits is
(A) 23
(B) 21
(C) 20
(D) 18
(E) 15
Six towns labelled \(P, Q, R, S, T\) and \(U\) in the diagram are joined by roads as shown.

Starting at \(P\), George the postman visits each town without returning to \(P\). He wants to save time by travelling the shortest distance. How many kilometres will he need to drive?
(A) 19
(B) 20
(C) 21
(D) 22
(E) 23
A set of 4-digit numbers are formed using four cards numbered 2,3 , 5 and 6 , with each number formed containing every digit. How many numbers in this set will be divisible by 8 ?
(A) 4
(B) 6
(C) 8
(D) 10
(E) 12
Mary has 62 square blue tiles and a number of square red tiles. All tiles are the same size. She makes a rectangle with red tiles inside and blue tiles on the perimeter. What is the largest number of red tiles she could have used?
(A) 62
(B) 182
(C) 210
(D) 224
(E) 240
Carly is writing a fantasy novel which includes inventing a new language. She decides to base her alphabet on letters formed from three straight lines joining four dots arranged in a square where each line joins two dots. Each letter goes through all four dots and can be drawn without removing the pencil from the paper, (you may retrace a line). Three such letters are shown.

How many different letters can she have in her alphabet?
(A) 12
(B) 16
(C) 24
(D) 32
(E) 36
What is the smallest number which is divisible by 7 and 6 and has two odd digits?
Which 2-digit number is equal to the sum of its first digit plus the square of its second digit?
Andrew thinks of 4 consecutive numbers. The sum of the first three numbers is 100 more than the fourth number. What is the sum of these four consecutive numbers?
Paul is one year older than his wife and they have two children whose ages are also one year apart. Paul notices that on his birthday in 2011, the product of his age and his wife's age plus the sum of his children's ages is 2011.
What would have been the result if he had done this calculation thirteen years before?
Joe the handyman was employed to fix house numbers onto the doors of 80 new houses in a row. He screwed digits on their front doors, numbering them from 1 to 80 . Then he noticed that there were houses already numbered 1 to 64 in the street, so he had to replace all the numbers with new ones, 65 to 144 . If he re-used as many digits as possible (where he could use an upside down 6 as a 9 and vice versa), how many new digits must he have supplied?