Australian Mathematics Competition - 2011 - Middle Primary - Grade 3 & 4 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesMike buys a can of 4 tennis balls for \(\$ 2\). How much does each tennis ball cost?
(A) 25 c
(B) 50 c
(C) \(\$ 1\)
(D) \(\$ 4\)
(E) \(\$ 8\)
The number 8000 is the same as
(A) 800 tens
(B) 800 units
(C) 80 tens
(D) 80 units
(E) 8 hundreds
One side of a square is 6 cm long. What is the perimeter, in centimetres, of this square?
(A) 6
(B) 18
(C) 24
(D) 26
(E) 30
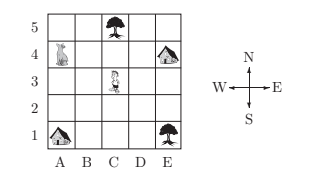
Imagine you are standing on the square which is in column C and row 4.
What can you see directly to the east?
What number is halfway between 103 and 113 ?
(A) 107
(B) 110
(C) 105
(D) 109
(E) 108
Ben cuts three oranges into quarters for the soccer team to eat at half-time. How many quarters are there?
(A) 3
(B) 6
(C) 7
(D) 12
(E) 16
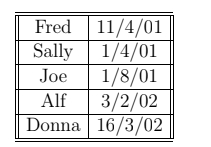
Mrs Harris asked five of her Year 4 children to record their birthdates in a table as shown below
Which child is the eldest?
(A) Sally
(B) Fred
(C) Joe
(D) Alf
(E) Donna
Gina is 11 years old and her sister Bev is 8 years old. Their mum is twice as old as the sum of their ages. How old is their mum?
(A) 3
(B) 19
(C) 27
(D) 30
(E) 38
How many rectangles of any size are in this
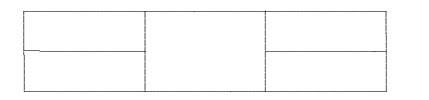
diagram?
(A) 11
(B) 10
(C) 9
(D) 8
(E) 6
I can buy 10 L of petrol for \(\$ 15\). How much do I pay for 40 L ?
(A) \(\$ 40\)
(B) \(\$ 55\)
(C) \(\$ 60\)
(D) \(\$ 65\)
(E) \(\$ 80\)
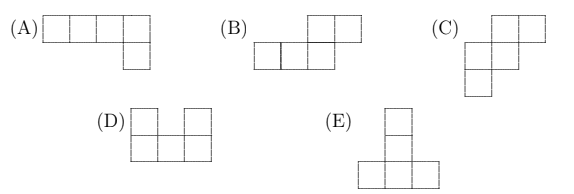
Which of the following is not a net for an open top box?
Peter and Sue travelled from Cairns to Brisbane by aeroplane. Their flight took 130 minutes. If they left Cairns at 8:10 am, what time did they arrive in Brisbane?
(A) 10:10 am
(B) 9:40 am
(C) 10:40 am
(D) 9:30 am
(E) \(10: 20 \mathrm{am}\)
Which one of the following statements is true?
(A) If you add two odd numbers you always get an odd number.
(B) If you multiply two odd numbers you always get an even number.
(C) If you add an odd and an even number you always get an even number.
(D) If you multiply an odd and an even number you always get an even number.
(E) If you multiply two even numbers you always get an odd number.
Zac bought four medium pizzas with \(\$ 20\) and received \(\$ 3.60\) in change. How much would two pizzas have cost him?
(A) \(\$ 4.10\)
(B) \(\$ 5.00\)
(C) \(\$ 7.20\)
(D) \(\$ 8.20\)
(E) \(\$ 10.00\)
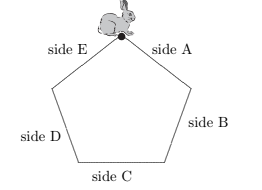
Raelene the rabbit started at the dot and travelled clockwise around the regular pentagon with equal sides.
What side was she on when she had travelled \(\frac{3}{4}\) of the distance around the pentagon?
(A) A
(B) B
(C) C
(D) D
(E) E
How many even two-digit numbers are there where the sum of the digits is 5 ?
(A) 0
(B) 2
(C) 3
(D) 4
(E) 5
The diagram shows a 7-piece tangram puzzle.

What is the area, in square centimetres, of the shaded part if the whole puzzle is a square with
side 8 cm ?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
On a school trip, we took 6 tents for 18 students. Each tent sleeps either two or four students. How many of the tents were for two students?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
The annual parents' meeting is held on the 199th day of the calendar year. In which month will the meeting be held in 2011?
(A) April
(B) May
(C) June
(D) July
(E) August
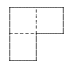
The following tile is made from three unit squares.
What is the area, in square units, of the smallest square which can be made from tiles of this shape?
(A) 16
(B) 25
(C) 36
(D) 64
(E) 81
A cube has each of the numbers from 1 to 6 on its faces. The cube is shown in three different positions.
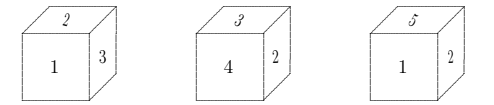
What number is on the opposite face to the face numbered \(6 ?\)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
In a number game you throw 2 six-sided dice to get 2 numbers from 1 to 6 . You then choose one instruction card from the three shown below to find out what to do with the two numbers.

How many different whole number answers are possible in this game?
(A) 13
(B) 15
(C) 17
(D) 20
(E) 21
In the following addition, some of the digits are missing.
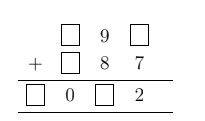
The sum of the missing digits is
(A) 23
(B) 19
(C) 21
(D) 18
(E) 24
The ages of a family of six add up to 106 years. The two youngest are 3 and 7 . What would the family's ages have added up to five years ago?
(A) 74
(B) 76
(C) 78
(D) 79
(E) 96
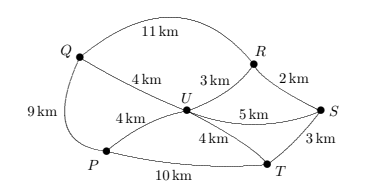
Six towns labelled \(P, Q, R, S, T\) and \(U\) in the diagram are joined by roads as shown.
Starting at \(P\), George the postman visits each town without returning to \(P\). He wants to save time by travelling the shortest distance. How many kilometres will he need to drive?
(A) 19
(B) 20
(C) 21
(D) 22
(E) 23
In a card game, there are 9 single-digit cards and 4 operation cards as shown.
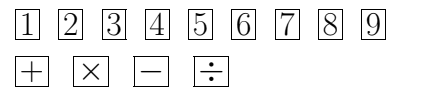
A player must use 4 digit cards and 3 operation cards. What is the largest whole number which can be made if an operation card must be placed between each of the single-digit cards?
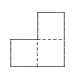
A tiler has been given an odd-shaped tile to work with. It is made up from 3 squares, each with 10 cm sides.
If he had 5 of these tiles and placed them next to each other to form a shape, what would be the smallest perimeter, in centimetres, that he could make?
Jacqui has \(\$ 200\) in her purse in \(\$ 5, \$ 10\) and \(\$ 20\) notes. She has 20 of these notes altogether. If she has more \(\$ 20\) notes than \(\$ 10\) notes, how many \(\$ 5\) notes does she have?
Mary has 62 square blue tiles and a number of square red tiles. All tiles are the same size. She makes a rectangle with red tiles inside and blue tiles on the perimeter. What is the largest number of red tiles she could have used?

Carly is writing a fantasy novel which includes inventing a new language. She decides to base her alphabet on letters formed from three straight lines joining four dots arranged in a square where each line joins two dots. Each letter goes through all four dots and can be drawn without removing the pencil from the paper, (you may retrace a line). Three such letters are shown.
How many different letters can she have in her alphabet?